Electromagnetic wave

|

|
|
|
Linearly polarized electromagnetic wave in a vacuum. The monochromatic wave with wavelength propagates in the x direction of the electric field strength (in blue) and the magnetic flux density (in red) to each other and to the propagation direction at right angles and form in this order, a legal system .
|
||
An electromagnetic wave , also known as electromagnetic radiation , is a wave made up of coupled electrical and magnetic fields. Sometimes radiation is also briefly referred to , although there is a risk of confusion with other particle radiation. Examples of electromagnetic waves are radio waves , microwaves , thermal radiation , light , X-rays and gamma rays (listed according to increasing frequency). Electromagnetic waves in a vacuum are transverse waves. The interaction of electromagnetic waves with matter depends on their frequency , which can vary over many orders of magnitude.
Unlike sound waves , for example , electromagnetic waves do not need a medium in order to propagate. They can therefore spread over the greatest distances in space . They move in a vacuum at the speed of light regardless of their frequency . Electromagnetic waves can also propagate in matter (e.g. a gas or a liquid), but their speed is reduced. The refractive index indicates the ratio by which the phase velocity of electromagnetic waves in matter is lower than the speed of light in a vacuum.
As transverse waves, electromagnetic waves show the phenomenon of polarization . In free space , the vectors of the electric and magnetic fields are perpendicular to each other and on the direction of propagation. The transversality may be violated if - as with plasma oscillations ( plasmons ) - carriers of chemical properties, e.g. B. metallic or bound electrons are involved. The sources, propagation properties and effects of the radiation differ accordingly in the various areas of the electromagnetic spectrum .
Emergence
Electromagnetic waves can arise from different causes:
- Spontaneous emission when the energy of an atom decreases. Energy changes in the atomic shell are usually orders of magnitude smaller than energy changes in the atomic nucleus. If the atom is “left alone” (as in dilute gases) during the period of energy radiation, a sharp line spectrum is created . This is not the case with high pressure, such as in ultra- high pressure lamps and xenon light or with atoms in solids. Well-defined spectral lines can no longer be measured there due to pressure broadening .
- Brake radiation : Electromagnetic waves are also created when charge carriers are accelerated. This happens, for example, in the plasma of the sun or in the X-ray tube .
- Molecular vibrations (periodic movements of neighboring atoms in a molecule)
- Larmor precession of a particle with a magnetic dipole moment around the direction of an externally applied magnetic field .
- A movement of electrically charged particles through a medium at high speed . If the speed of the particles is greater than the phase speed of electromagnetic waves in this medium, Cherenkov radiation is created .
- A time-varying electric current emits electromagnetic waves. In radio technology , this is used with transmitting antennas for the wireless transmission of signals.
- In pair annihilation , matter is converted into electromagnetic radiation. The energy of the radiation results from the mass and the kinetic energy of the particles.
properties
Identify and measure the presence of electromagnetic waves
Receivers for electromagnetic radiation are called sensors or detectors , and in living beings, photoreceptors . Radio waves can be detected by antennas .
Which can be an electromagnetic wave to wave velocity measure, on the one hand in the vacuum universal constant speed of light , as well as deviating values for the phase velocity in a transmissive (transparent) medium. The intensity can also be measured, which is equivalent to the power or the energy transported per unit of time through a specific cross section .
There are different methods of measuring the wavelength, depending on whether it is shorter or longer wavelengths. Wavelength and frequency can be passed through
convert into each other.
Wave character
From a physical point of view, electromagnetic waves are propagating oscillations of the electromagnetic field. In the case of linearly polarized waves , the electric and magnetic fields are perpendicular to one another and have a fixed size ratio, which is given by the wave impedance . In particular, the electric and magnetic fields disappear in the same places at the same time, so that the frequently read representation that electric and magnetic energy are cyclically converted into one another is not correct in the far field . However, it is correct, for example, for the near field of an electric dipole or resonant circuit that generates electromagnetic waves .
The origin of electromagnetic waves can be explained by Maxwell's equations : The change in the electric field over time is always linked to a spatial change in the magnetic field. Likewise, the change in the magnetic field over time is again linked to a spatial change in the electric field. For fields that change periodically (especially sinusoidally ), these effects together result in a progressive wave.
Examples of experiments in which the wave character comes into play:
- Phenomena such as coherence and interference can only be explained with the wave model, because the phase of the wave is needed for this.
- Antennas for the radiation emitted by radio transmitters are matched to the size of the wavelength. For example, an efficient dipole antenna is half the length of the wavelength. A description of the radiation as a very large number of photons offers no advantage, since there is no measuring device to individually detect such low-energy photons.
Particle character
For certain properties of electromagnetic waves (e.g. photoelectric effect ), the wave model described above is not sufficient to describe all observable phenomena, rather the particle properties of individual photons , the quanta of the electromagnetic field, come to the fore. The wave character (e.g. interference ) remains fully intact. One therefore speaks of the dualism of particle and wave .
Within the framework of this concept of light as a particle, each frequency is assigned the energy of a single photon , which is Planck's quantum of action . On the other hand, particles, such as electrons moving across several atoms , also have wave properties (see also electrical current ). Both aspects of electromagnetic waves can be explained in terms of quantum electrodynamics .
Examples of effects in which the particle character comes into play:
- In the Compton effect , an electromagnetic wave with a wavelength of around 20 pm hits an electron whose cross-section is around three orders of magnitude smaller. To explain the physical course of the interaction, the particle character of the light must be used. Any attempt to explain the observed change in wavelength with the wave model fails.
- With the photoelectric effect , the kinetic energy is not dependent on the amplitude of the radiation, but increases linearly with the frequency. This can only be explained by the particle character.
- The generation of laser light is based on the properties of individual atoms, which are each smaller than the wavelength generated. Therefore one has to fall back on the photon model to explain the production .
Photons with sufficient energy (e.g. from a few electron volts upwards) have an ionizing effect on matter and can trigger chemical ( photochemical ) effects if the binding energies are exceeded ( photochemistry ). This chemical effectiveness is also known as actinity .
Waves in the medium
The phase velocity with which a monochromatic wave moves in a medium is typically lower than in a vacuum. In a linear approximation it depends on the permittivity and the permeability of the substance,
and is therefore dependent on the frequency of the wave (see dispersion ) and, in the case of birefringent media, also on its polarization and direction of propagation. The influence of static fields on the optical properties of a medium leads to electro- optics or magneto-optics .
A direct force effect (e.g. change of direction) on a propagating electromagnetic wave can only take place through the medium of propagation (see refraction , reflection , scattering and absorption ) or be mediated (see nonlinear optics and acousto-optical modulator ).
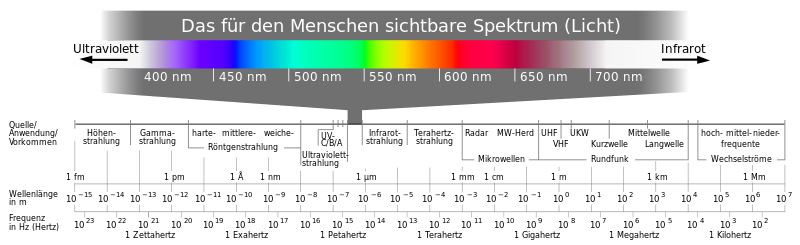
spectrum
Electromagnetic waves are classified according to their wavelength in the electromagnetic spectrum . A list of frequencies and examples of electromagnetic waves can be found in the corresponding article.
Visible light represents only a small part of the entire spectrum and, with the exception of infrared radiation (heat), is the only area that can be perceived by people without technical aids. At lower frequencies, the energy of the photons is too low to trigger chemical processes. At higher frequencies, however, the range of ionizing radiation ( radioactivity ) begins , in which a single photon can destroy molecules. This effect already occurs with ultraviolet radiation and is responsible for the formation of skin cancer with excessive sun exposure.
With light, the frequency determines the color of the light and not, as is often wrongly assumed, the wavelength in a medium during propagation. In contrast to the wavelength, the frequency is not influenced during the transition into optically denser media. Since the color does not change when it passes through a medium, only the frequency is characteristic of the color of the light. For historical reasons, however, the wavelength is given as a characteristic property in spectra. The relationship between color and wavelength only applies in a vacuum and to a good approximation in air. Monochromatic light , i.e. light with only a single wavelength, always has a spectral color .
Biological and chemical effects

When it comes to the interaction of electromagnetic radiation with biological matter, a distinction must be made between ionizing radiation (greater than 5 eV) and non-ionizing radiation. With ionizing radiation, the energy is sufficient to ionize atoms or molecules, i. H. Knock out electrons. This creates free radicals that cause biologically harmful reactions. If the energy of photons reaches or exceeds the binding energy of a molecule, each photon can destroy a molecule, so that, for example, accelerated aging of the skin or skin cancer can occur. Chemical binding energies of stable molecules are above about 3 eV per binding. If the molecules are to change, photons must have at least this energy, which corresponds to violet light or higher frequency radiation.
When it comes to the interaction of non-ionizing radiation, a distinction is made between thermal effects (radiation has a warming effect because it is absorbed by the tissue ), direct field effects (induced dipole moments, changes in membrane potentials), quantum effects and resonance effects (synchronization with the oscillation of the Cell structure).
A photon with a wavelength of 700 nm or shorter can cause the conformation of the rhodopsin molecule to change . In the eye of this change is recorded and processed as a signal from the nervous system. The sensitivity for a certain wavelength changes with modifications of the rhodopsin. This is the biochemical basis of the color sense . Photons of light with a wavelength above 0.7 µm have an energy below 1.7 eV. These waves cannot cause chemical reactions on molecules that are stable at room temperature. Because of this, animal eyes usually cannot see infrared or thermal radiation. In 2013, however, researchers discovered that the cichlid Pelvicachromis taeniatus can see in the near-infrared range. There are also other sense organs for infrared radiation, such as the pit organ in snakes .
Photons can excite vibrations in molecules or in the crystal lattice of a solid . These vibrations make themselves felt in the material as thermal energy . Additional vibrations excited by electromagnetic waves increase the temperature of the material. In contrast to the effect of individual photons on chemical bonds, what matters here is not the energy of the individual photons, but the sum of the energy of all photons, i.e. the intensity of the radiation. Long- wave electromagnetic radiation can indirectly change biological substances through heat denaturation .
Speed of light and special relativity
How fast does light about spreads , was known since 1676th However, until 1865 there was no connection to other physical phenomena. James Clerk Maxwell was able to produce this between 1861 and 1862 using the Maxwell equations he found , which predict the existence of electromagnetic waves. Their speed agreed so well with the then known speed of light that a connection was immediately established. Heinrich Hertz was able to demonstrate these waves experimentally in the 1880s.
In classical mechanics, waves (in the direction of propagation ) are defined by the wave equation
described. The term here refers to the deflection of the wave and its phase velocity , which can be interpreted as the propagation velocity of the wave.
From Maxwell's equations, the relationship for the electric field strength in a vacuum can be :
derive (in SI units ; see section Mathematical Description ). In this respect the electric field strength behaves like a wave; the size
occurs as the speed of propagation. This speed is composed exclusively of natural constants that are independent of the observer's reference system, which is consequently transferred to the size .
The basis of classical mechanics is the Galilean principle of relativity , which states that the laws of nature in all inertial systems - those reference systems in which bodies that are not subject to any force move in a straight line - have the same form ( Galileo invariance ). A reference system moving to an inertial system at constant speed is also an inertial system.
According to this principle of relativity, it would be expected that an observer moving at a constant speed relative to the electromagnetic wave would measure a different speed of propagation, such as a walker walking at a constant speed on the edge of a pond would notice a different speed of propagation of a water wave on the pond would as a dormant observer. The Maxwell equations predict the same speed of propagation for both observers - they are not Galileo-invariant.
This contradiction to classical mechanics is resolved in favor of Maxwell's equations: The fact that electromagnetic waves propagate in all inertial systems with the same speed - the much-cited constancy of the speed of light - is a postulate in Einstein's special theory of relativity published in 1905 . The so-called Lorentz invariance replaces the Galileo invariance .
Mathematical description
The electromagnetic wave equation results directly from Maxwell's equations and the freedom from divergence of electromagnetic waves and reads in a vacuum
- .
If one considers the propagation of electromagnetic waves in polarizable media, the polarization must also be considered:
Derivation of the electromagnetic wave equation
The mathematical relationships associated with wave propagation can be understood on the basis of Maxwell's equations. In particular, the same form of the wave equation can be derived with which other types of waves, for example sound waves, propagate.
In a vacuum, i.e. in a charge-free space with the exclusion of dielectric , dia- and paramagnetic effects, the material equations of electrodynamics and . In addition, the current density and charge density are zero.
Based on Maxwell's third equation
|
|
|
(1)
|
|
|
one applies the rotation operator to both sides . This gives:
- .
If one inserts the fourth Maxwell's equation into it ,
- ,
surrendered
|
|
|
(2)
|
|
|
The vector-analytical relationship applies in general to this
- .
Here, with the application of the vectorial Laplace operator on the vector field meant. In Cartesian coordinates, the vectorial Laplace operator acts like the scalar Laplace operator on every component of .
If one applies this relation and takes into account that the charge-free space is considered, in which the divergence is zero according to Maxwell's first equation , then it follows:
|
.
|
|
(3)
|
|
|
If you now put (2) and (3) together, the following wave equation results :
|
.
|
|
(4)
|
|
|
Almost all waves can be expressed by equations of form
describe, where is the speed of propagation of the wave. The following applies to the speed of propagation of electromagnetic waves, the speed of light :
- .
This gives the equation from (4)
- .
Analogously, the relationship for the magnetic flux density can be
derive. The solutions to these equations describe waves that propagate in a vacuum at the speed of light . If the electromagnetic wave propagates in an isotropic material with the dielectric constant and the permeability , the speed of propagation is
- .
In general, however, the material constants are not linear, but can depend on the field strength or the frequency. While light propagates in the air almost at the speed of light in a vacuum (the material constants are a good approximation 1), this does not apply to the propagation in water, which among other things enables the Cherenkov effect .
The ratio of the speed of light in a vacuum to the speed in the medium is called the refractive index .
- ,
where and denote the relative permeability and the relative permittivity of the medium.
Propagation of electromagnetic waves
With the help of Maxwell's equations, further conclusions can be drawn from the wave equation. Let us consider a general plane wave for the electric field
- ,
where is the (constant) amplitude, an arbitrary C 2 function , a unit vector pointing in the direction of propagation, and a position vector. First, by inserting it into the wave equation, one sees that the wave equation satisfies, i.e. that
- .
In order to describe an electromagnetic wave, it not only has to fulfill the wave equation, but also the Maxwell equations. That means
- ,
- .
The electric field is always perpendicular to the direction of propagation, so it is a transverse wave . Substituting into another Maxwell equation gives
and there is, it follows
- .
The magnetic flux density in the electromagnetic wave is also perpendicular to the direction of propagation and also perpendicular to the electric field. In addition, their amplitudes are in a fixed relationship. Their quotient is the speed of light
- .
In natural units ( ), both amplitudes have the same value.
With this relationship a statement can be made about the energy density
derive the electromagnetic field for the case of the electromagnetic wave:
- .
Not every electromagnetic wave has the property that its direction of propagation and the directions of the electric and magnetic fields are orthogonal to one another in pairs, i.e. the wave is a pure transverse wave , also known as a TEM wave . The plane waves demonstrated here are of this type, but there are also waves in which only one of the two field vectors is perpendicular to the direction of propagation, but the other has a component in the direction of propagation ( TM and TE waves ). An important application for such non-purely transverse electromagnetic waves are cylindrical waveguides . What has been said applies above all to crystals with birefringence . However, there are no purely longitudinal electromagnetic waves.
literature
- John David Jackson : Classical Electrodynamics . 4th edition. de Gruyter, Berlin a. a. 2006, ISBN 3-11-018970-4 .
- Karl Küpfmüller , Wolfgang Mathis , Albrecht Reibiger: Theoretical electrical engineering. An introduction. 16th edition. Springer, Berlin a. a. 2005, ISBN 3-540-20792-9 .
- Claus Müller : Basic problems of the mathematical theory of electromagnetic oscillations (= The basic teachings of the mathematical sciences in individual representations. 88, ISSN 0072-7830 ). Springer, Berlin a. a. 1957.
- Eduard Rhein : Miracle of the waves: Rundfunk u. Television, shown f. jedermann , issue 69. – 80. Th., German publ. D. Ullstein AG, Berlin-Tempelhof 1954. DNB
- Károly Simonyi : Theoretical electrical engineering. 10th edition. Barth, Leipzig a. a. 1993, ISBN 3-335-00375-6 .
Web links
- Experiments and tasks at student level ( LEIFI )
- Simple simulation of the propagation of electromagnetic radiation
- Clear derivation of electromagnetic waves from the Maxwell equations, almost free of formulas
Individual evidence
- ↑ Gerthsen Physics . 22nd, completely revised edition. Springer, Berlin a. a. 2004, ISBN 3-540-02622-3 , p. 177.
- ↑ Kenneth R. Foster, Michael H. Repacholi : Biological Effects of Radiofrequency Fields: Does Modulation Matter? In: Radiation Research. Vol. 162, No. 2, 2004, pp. 219-225, JSTOR 3581139 .
- ↑ Henrik Bohr, Søren Brunak, Jakob Bohr: Molecular wring resonances in chain molecules. In: Bioelectromagnetics. Vol. 18, No. 2, 1997, pp. 187-189, doi : 10.1002 / (SICI) 1521-186X (1997) 18: 2 <187 :: AID-BEM13> 3.0.CO; 2-O .
- ^ Walter Hoppe, Wolfgang Lohmann, Hubert Markl , Hubert Ziegler (eds.): Biophysik. 2nd, completely revised edition. Springer, Berlin a. a. 1982, ISBN 3-540-11335-5 .
- ↑ Reinhard Wandtner: First evidence in animals: Infrared when catching prey . In: Frankfurter Allgemeine Zeitung . February 4, 2013 ( faz.net ).
- ^ M. Guarnieri: Two Millennia of Light: The Long Path to Maxwell's Waves . In: IEEE Industrial Electronics Magazine . 9, No. 2, 2015, pp. 54–56 + 60. doi : 10.1109 / MIE.2015.2421754 .
- ↑ More details on crystal optics ( birefringence, etc.) in: W. Döring, Göschen-Bändchen zur Theoretischen Physik, volume "Optik".