Magnetic flux density
| Physical size | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Surname | Magnetic flux density | |||||||||||||||
| Formula symbol | ||||||||||||||||
|
||||||||||||||||
The magnetic flux density , also called magnetic induction , sometimes just called “flux density” or “magnetic field” or “ B field” in technical colloquial language , is a physical quantity of electrodynamics . It is the areal density of the magnetic flux that passes perpendicularly through a certain area element.
The magnetic flux density at a location is - like the electrical flux density - a directed quantity, i.e. a vector , and is derived from the vector potential .
Definition and calculation
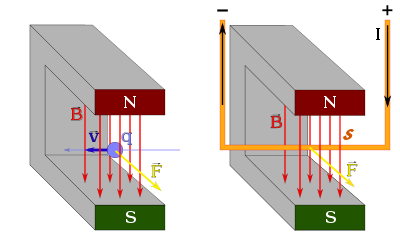
Like the electric field strength , the magnetic flux density is historically indirect, i.e. H. defined by their experimentally measurable force effect on moving electrical charges, which in modern physics is regarded as the magnetic component of the Lorentz force and is notated in vector notation as follows:
With:
- - movement-related force effect on the charge in the magnetic field
- - electrical charge , or - amperage
- - the speed of the charge movement, or - the length of the path of the electric current through the investigated conductor (the orientation of depends on the technical direction of the current )
- - magnetic flux density
The first of the two equations listed above is mainly used for charges that can move freely in space, e.g. B. electrons within a Braun tube , used, the second, however, for charges that are within electrical conductors, z. B. wires or cables move. Both equations are equivalent.
In the formulas mentioned there is a vector which points in the direction of the field lines of the generating magnetic field.
If you do not use the vector notation and thus the possibility of determining the direction of the force effect from the vector product of the two vectors and or and , the following formula can also be used to calculate a scalar variable:
With:
- - electrical charge, or - amperage
- - speed of charge movement, or - length of the path of the current in the conductor
- - Magnitude of the magnetic flux density
- - Angle between the direction of the charge movement and the direction of the magnetic flux, or between the direction of the current flow and the direction of the magnetic flux.
The electric charge moves with the velocity perpendicular to the direction of the magnetic flux and / or extends the examined electrical conductor perpendicular to the magnetic flux direction, since in this case, assumes the value 1, the numerical value of the following equation directly from the force action on the load or the conductor can be calculated as a whole:
The relationship with the magnetic field strength is:
- .
Here is the magnetic permeability .
Measurement
The magnetic flux density can be measured with magnetometers , Hall sensors or measuring coils.
Unit of measurement
The SI unit of the magnetic flux density is the Tesla with the symbol T:
An outdated unit for the magnetic flux density is also the Gauss with the unit symbol G, which is still used in technology. 1 T = 10000 G applies.
Special cases
For the sake of simplicity, only the amounts of the flux densities are given below.
- magnetic flux density at a distance from a straight current-carrying conductor:
- (The direction of the flux density results from the corkscrew rule .)
- inside a long coil:
- (Here are the number of turns and the length of the coil. Strictly speaking, this is only an approximation formula that only applies under the following conditions: The length of the coil is large compared to the radius of the coil, the turns are very dense and uniform, and the location under consideration is inside the coil and not near the coil ends. The direction of the flux density runs parallel to the coil axis. For orientation see there . Outside the coil, the flux density is almost zero.)
- in the middle of a Helmholtz coil with a radius :
- at some distance from a magnetic dipole with the dipole moment :
- (The dipole moment of a circular conductor loop with the oriented cross-sectional area is .)
Magnetic flux dense and magnetic flux
The magnetic flux density is linked to the magnetic flux as area density via the following relationship :
The fact that the flux lines of the magnetic flux are self-contained can be expressed mathematically by the fact that every area integral of over any closed surface takes on the value 0:
Mathematically speaking, this equation is a direct consequence of Maxwell's homogeneous equation
as well as Gauss's theorem
for any vector field and the volume enclosed by .
To put it clearly: If you imagine a volume enclosed by a closed surface of any shape in a magnetic field, just as much “magnetism” always flows out through the surface as it does in from outside. This is referred to as " freedom from sources of the magnetic field".
literature
- K. Küpfmüller, G. Kohn: Theoretical electrical engineering and electronics, an introduction. 16., completely reworked u. updated edition. Springer, 2005, ISBN 3-540-20792-9
Web links
- Online flux density calculation from IBS Magnet as well as other formulas and downloads of magnet calculation tables.




























![{\ displaystyle \ left [B \ right] = 1 \, \ mathrm {T} = 1 \, {\ mathrm {Vs} \ over \ mathrm {m ^ {2}}} = 1 \, {\ mathrm {N } \ over \ mathrm {Am}} = 1 \, {\ mathrm {kg} \ over \ mathrm {As ^ {2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/06ddab5f8beee9c94a1f0ebb74273cd627df3e53)

















