Electric charge
| Physical size | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Surname | electric charge | |||||||||||||||
| Formula symbol | ||||||||||||||||
|
||||||||||||||||
The electric charge (amount of electricity) is a physical quantity that is associated with matter , e.g. B. also the mass . It determines the electromagnetic interaction , i.e. how matter reacts to electrical and magnetic fields and creates them. Your formula symbol or is derived from the Latin word ' quantum '. In the international system of units , the charge is given in the derived unit coulomb (= ampere second).
The electric charge is one of several types of charge that appear on elementary particles . Elementary particles can carry positive, negative or no electrical charge. The charge of free particles is always an integral multiple of the elementary charge , which is. The charge of the electron is negative: that of the proton positive . In the case of composite particles such as atoms , the individual charges add up. If the total charge is zero, the composite particle is called neutral . In a closed system , the total charge cannot be changed ( charge retention ). Within the framework of the theory of relativity, the charge of a particle is the same in every reference system, i.e. a Lorentz invariant .
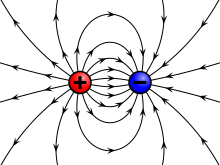
The electrostatic considered dormant charges and pure electric fields . The Coulomb force between positively and negatively charged bodies is attractive, between charges of the same name it is repulsive. Extensive physical systems always contain about the same number of positive and negative elementary charges. Even relatively small excess charges can cause considerable field strengths and forces (e.g. thunderstorms ).
Moving electrical charges form an electrical current . They generate electromagnetic fields and their movement is influenced by them. This behavior is described in classical electrodynamics .
On the microscopic level, the electromagnetic interaction between charges together with quantum mechanical effects such as the Pauli principle is the cause of the cohesion and structure of matter.
Everyday observations
Almost all physical phenomena that can be observed in everyday life are based on one of two fundamental interactions , gravity or the interaction of electrical charges. Electrical forces between the electron shells of atoms are essential to explain chemical processes and the properties of matter that can be experienced in general - even if quantum mechanical properties such as spin must often be taken into account to fully understand them.
Charged objects can also make themselves felt through forces. If packaging material, for example small pieces of polystyrene , appears to move by itself, it is due to the electrostatic attraction or repulsion of charged particles.
An impressive series of electrical charges by frictional electrification are thunder lightning . Air is usually an insulator , but breakdown occurs at high voltage . In lightning, there is a sudden charge equalization between differently charged areas in the thunderstorm cell or - less often - between an area in the thunderstorm cell and the ground. Small sparks that are accompanied by a crackling sound can also arise when putting on and taking off clothes or when combing.
Humans have no specific sense organ for electrical charge. He can only perceive it indirectly when the current through the body or the voltage dropping across the skin resistance reaches the threshold value of the action potential of the neurons . As mentioned above, a slight electric shock can be felt when taking off items of clothing or when walking over a carpet and then touching a door handle. Electric current can trigger pulling pain in the tooth nerve if electrochemically different metals (e.g. aluminum foil and amalgam ) are in contact in the mouth and a local element is formed. In the same way, a tingling sensation in the tongue is caused by the flow of current if you touch both poles of a suitable battery with a wet tongue .
history
Naming
Presumably as early as 550 BC. In ancient Greece, Thales von Milet carried out experiments in which the forces emanating from electrical charges were observed. For example, a piece of amber (Greek ηλεκτρόν - pronounced electron ) was found to have an attractive force on bird feathers or hair after the amber had been rubbed on a dry fur.
Queen Elizabeth I's court physician , William Gilbert , continued the work of Petrus Peregrinus from the 13th century and found out that other substances can also be electrified by friction. He led in his 1600 book, De magnets Magnetisque corporibus, et de Magno Magnets Tellure (German about: About the magnet magnetic body and the large magnet Earth ) to the New Latin borrowed term "electrica" for the appearances, which he in Connection with the amber discovered. This term was later used as an electron to denote the carrier of the negative elementary charge, the electron so named by George Johnstone Stoney in 1891 and detected by Joseph John Thomson in 1897 (rubbed amber also takes on a negative charge).
One or two types of cargo

William Gilbert is considered the founder of electricity because of his work. He was the first to differentiate between electrical and magnetic attraction. His explanation for the attraction of a rubbed amber to other bodies was that he assumed an “imponderable” (imponderably light) fluid found in all bodies that can be influenced by friction, which escapes through the heat during friction and surrounds the body like a cloud of vapor . Other substances would be attracted when penetrating this vapor, analogous to the attraction of a stone by the earth. From today's point of view, Gilbert's fluid theory or fluid hypothesis suggests something of the modern concept of the field . However, the differences are considerable, especially because the haze consists of leaked fluid. Otto von Guericke dealt with static electricity in his later work, but little of his results has survived. In 1672 he invented a simple electrifying machine , with the help of which he could observe a whole series of phenomena, such as influence , the conduction of electrical charge, the luminous effect ( electroluminescence ) and the fact that two bodies electrified with the same name repel one another. Until then, we only knew about the attraction of electricity; Gilbert's attempt to explain the one fluid was no longer sufficient.
Charles du Fay discovered in 1733 in experiments with static electricity that the two types of electricity could neutralize each other. He designated the types of electricity as glass electricity ( French électricité vitreuse ) and resin electricity ( French électricité résineuse ). Glass electricity in today's terminology corresponds to the positive charge. From these experiments, Jean-Antoine Nollet developed the so-called “two-fluid theory” or dualistic theory, as also represented by Robert Symmer . Accordingly, the two types of electricity surround the electrified bodies as "two fluids" (the effluvium and the affluvium ). According to this theory, an electrically neutral body contains the same amount of both fluids. When two bodies come into close contact, positive fluid passes from one body to the other, while the other body releases the same amount of negative fluid to the first. This way of speaking shaped thinking about the nature of electricity in the 18th century and still lives on today in the "two types of charge" (positive charge vs. negative charge).

Im from Benjamin Franklin - on the subject of electrical phenomena - authored book Experiments and Observations on Electricity that coined the term charge (Engl. Batch ). Before we had to speak of “bodies that have been put into an electrical state”. Franklin introduced a view similar to that of the debited and unencumbered account, where redistribution occurred due to friction. William Watson came to a similar conclusion at the same time. According to this unitary theory or Einflüssigkeitstheorie therefore is the only fluid in a specific normal quantity in electrically neutral appearing bodies present. When two bodies rub against one another, a certain amount of this fluid is transferred from one body to the other, so that the change in the location of the fluid causes one body to be positively charged and the other equally negatively charged. Franklin could not explain with his point of view why two bodies equally emptied of charge repel each other, only Franz Ulrich Theodor Aepinus remedied this deficiency. In today's language, he saw the particles of matter in a kind of ionized state when the charges were removed.
Franklin's assumption that the electricity of glass exists and the resin electricity is a deficiency and that when charged and uncharged bodies are touched, the electricity only flows in one direction, suggests that - in today's terminology - the positive charges are always each other move. Presumably Franklin was led to this assumption by the type of luminous phenomena observed in his experiments with charged metal tips.
With this new theory of electricity as “one fluid”, the idea of charge retention was given a breakthrough. The charges are not generated by friction, but only separated from each other. Since the direction of force between two charges can be described simply with the sign of the charges involved using the two-liquid model, Charles Augustin de Coulomb adopted the dualistic model of the “two fluids” and based the existence of two types of charges . From today's perspective, you can get the same result with both models.
In the German-speaking countries, Franklin's designation was probably mainly spread by Leonhard Euler and Georg Christoph Lichtenberg .
Quantitative experiments

Robert Boyle found in 1675 that electrical attraction or repulsion also occurs through a vacuum, Francis Hauksbee deepened these investigations using electrical luminous phenomena in a vacuum. Stephen Gray divided materials into electrically conductive and electrically insulating in 1729 and demonstrated that the human body could also conduct electricity.
In the last quarter of the 18th century, the focus of the meanwhile (after an impressive experimental tool had been found in the Leiden bottle ) shifted to the very popular discussion of electricity theory towards quantitative studies of electrostatics. Special contributions to the research were made by Joseph Priestley and Charles Augustin de Coulomb . In 1785, Coulomb published Coulomb's law , which states that the amount of this force between two charged spheres is proportional to the product of the two amounts of charge and inversely proportional to the square of the distance between the centers of the spheres. Depending on the sign of the charges, the force has an attractive or repulsive effect in the direction of the straight line connecting the center points.
Faraday's laws formulated by Michael Faraday in 1832 establish a connection between the electrical charge that has flowed and the metabolism ( amount of substance deposited on the electrodes ) during electrolysis . In a lecture given to the Royal Society in 1833 , Faraday demonstrated that the “static” (or “ordinary”), the “atmospheric”, the “physiological” (or “animal”), the “Voltaic” (or “touch electricity”) and “thermoelectricity” were in truth just different aspects of the one physical principle he called “magnetic electricity”. Thus it was also clear that the electric charge is the basic property of matter for all these phenomena. An important contribution by Michael Faraday to the theory of electricity was the systematic introduction of the term field to describe electrical and magnetic phenomena.
In 1873, Frederick Guthrie discovered that a positively charged electroscope would discharge if you bring a grounded, glowing piece of metal near it. With a negatively charged electroscope, nothing happens, which means that glowing metal only emits negative charge and this electric current can only flow in one direction. Thomas Edison rediscovered this phenomenon in 1880 during experiments with incandescent lamps and in 1883 applied for a patent for an application based on it. The "glowing electrical effect" is called the Edison-Richardson effect after Edison and Richardson , who was awarded the Nobel Prize in 1928 for the declaration .
In 1897 Joseph John Thomson was able to prove that cathode rays consist of electrons. With a greatly improved vacuum , he was able to determine the charge-to-mass ratio for these. Thomson assumed that the electrons were already present in the atoms of the cathode , and in 1903 he set up an atomic model for the first time that ascribed an internal structure to the atoms.
The discrete character of the electrical charge, which had been predicted by Faraday in the course of his electrolysis experiments in the 19th century, was confirmed in 1910 by Robert Andrews Millikan in the so-called Millikan experiment . In this experiment it was demonstrated that charged oil droplets are always charged with an integral multiple of the elementary charge; it also provided a useful numerical value for the size of the elementary charge.
Properties of the electric charge
Total charge
The electrical charge can assume positive or negative values. One often speaks of two types of electrical charge. For example, an electron or a muon has the charge −1 e , a positron or a proton the charge +1 e.
A particle and its antiparticle have exactly the same amount of charge. For example, the antiproton , antiparticle of the proton, carries the charge −1 e.

The absolute charge of a body or a quantity of substance is the sum of all elementary charges it contains. The terms total charge, net charge or excess charge are also used for this. The meaning of this term is based on the fact that the electrical effects of positive and negative charges cancel each other out if their mutual distance is negligibly small compared to the distance to the effective site. The lithium ion shown acts like a single charge carrier with a single positive charge at intervals of a few nanometers and is also written as Li + . The cancellation also works exactly with hundreds of billions of charge carriers, such as the Millikans oil droplets already described .
On the one hand, a particle that has no charge is referred to as electrically neutral (for example a neutron , gray in the lithium atom image). On the other hand, a body is also called neutral if it has an equal number of positive and negative elementary charges, such as a helium atom with two protons and two electrons.
One speaks of charge separation when charges of one sign predominate in certain areas of space, i.e. when the absolute charge is not zero there. In the case of charge separation within a body or component, the indication of the total charge is not sufficient. For example, the total charge of both the charged and uncharged capacitors can be zero. But while the plates of the uncharged capacitor are each electrically neutral, the plates of the charged capacitor carry oppositely equal excess charges, which above all generate an electric field between the plates. Any oil droplets present there are polarized .
Charge retention
Preservation of charge is understood to mean the phenomenon that in every closed system the amount of electrical charge that is present remains constant over time. This phenomenon has consequences: If matter is created from electromagnetic radiation or photons , then this must be done in such a way that no charge is generated. For example, an electron and its antiparticle, the positron, are created at the same time during pair formation . This means that the total charge generated is zero and the amount of charge is retained. The same applies to the reverse of this process, the annihilation of a particle-antiparticle pair, in which the total annihilated charge is also zero.
As with any fundamental law of conservation of physics , the law of conservation of electric charge is based on observation and experiment. So far, all relevant experiments have confirmed the electrical charge conservation - in some cases with very high accuracy. In the formal theoretical description of electrodynamics, the conservation of charge is expressed by a continuity equation, which is a consequence of Maxwell's equations (see section Charge and Electric Current ). A more abstract property of electrodynamics is its invariance (often also called symmetry ) under gauge transformations , from which quantum electrodynamics as gauge theory results. According to Noether's theorem , the invariance of electrodynamics under gauge transformations is also linked to the electric charge as a conservation quantity.
In the apparent contradiction to the maintenance of the charge, there is the expression of a charge generation or charging. But this means a local accumulation of charges of one sign, i.e. actually a charge separation (and no generation).
Charging
In order to charge (in the sense of an excess charge) a previously neutral body, it must absorb or release charge carriers. But even with an uneven charge distribution in an overall neutral body, one speaks of “charging”. This happens due to an applied electric field or through movements on a molecular scale. In the case of a polarized material, the charge is bound; in the case of influence , “freely movable” charge carriers are shifted in a conductor.
A mechanism for separating charges known from everyday life is friction . For example, if you rub a balloon on a sweater, electrons are transferred from one material to the other, so that the electrons and the remaining atomic core are separated. Such static electricity is a special case of contact electricity . The band generator uses both touch electricity and induction.
In batteries and accumulators , chemical reactions are used to redistribute a large number of charge carriers (electrons or ions ). As with the capacitor, the total charge remains zero. In contrast to this, however, the voltage does not increase almost linearly, but remains roughly constant. This is why the capacity of a capacitor as an energy storage device is given in Farads (= coulombs per volt), while the capacity of a battery is characterized as the amount of charge - in ampere-hours , where 1 ampere-hour equals 3600 coulombs.
Charge separation can also be caused by electromagnetic waves , for example light : If light is allowed to hit a metal surface with a sufficiently high frequency and a second metal plate is placed nearby in a vacuum, a charge difference arises between them because the light causes electrons from the first plate which partially move to the second plate ( external photoelectric effect ).
Relativistic invariant
The charge on a body is not only a conserved quantity, but also independent of its speed . That means that the electric charge is a relativistic invariant , the total charge of an object is not changed by the length contraction . Charge has this property in common with the invariant mass of a system, but distinguishes it from energy, for example . From this example one can see that relativistic invariance is not a matter of course even for conserved quantities, but is an additional property.
On a computational level, the relativistic invariance of the charge can be understood by taking it as a volume integral over the charge density :
Under a Lorentz transformation, the charge density is transformed like the time component of a four-vector, ie it experiences a change analogous to the time dilation; the volume element , on the other hand, experiences a Lorentz contraction. These two effects cancel each other out so that the charge itself remains unchanged.
Interference experiments (for example by Claus Jönsson ) with electrons at different speeds show directly that their charge is independent of the speed. In addition, the charge of a solid would otherwise have to change with a change in temperature, because the speed of its components has increased due to the increased thermal energy , but the electrons receive a much higher speed on average than the more massive positive atomic nuclei. Also, hydrogen molecules and helium atoms (both contain two protons and two electrons) is electrically neutral, although the relative rates of their components differ significantly.
Quantum character
Electrically charged matter cannot carry any amount of charge. The charges of all known elementary particles have been measured experimentally with the result that all leptons and their antiparticles always carry integer multiples of the elementary charge. Of the building blocks of atoms, protons and electrons carry the charge and the neutron no (electrical) charge. Quarks carry the charge or , but quarks never appear freely (see confinement ), but always only in bound states , the hadrons , which in turn always carry integer multiples of the elementary charge . Thus, all freely occurring particles carry integer multiples of the elementary charge.
Theoretically, this is justified in the electroweak model in that the electric charge is attributed to the weak hypercharge and the weak isospin . However, why the weak hypercharge and the weak isospin only assume certain values cannot be explained by the model. Therefore, the “cause” of the observed quantization of the charge has not yet been clarified; According to John David Jackson, it is one of the greatest mysteries in physics. According to Paul Dirac's consideration of a magnetic monopole , the existence of such a particle - and thus magnetic charges - would relate the charge quantization to the quantization of the angular momentum . Considerations from quantum field theory lead charge quantization back to the requirement that the standard model be free from anomalies .
Outside of atomic structures, it is usually permissible to view the charge as a continuous quantity . Even a tiny current of 1 nanoampere means a directional charge transport of around six billion electrons per second. This means that individual elementary charges cannot be identified in most aspects of electrical engineering. An exception is the "shot noise" .
Electric charge in quantum field theory
In the context of quantum field theory, the elementary charge is the coupling constant of the electromagnetic interaction. From the perspective of the renormalization group , however, the coupling constants of quantum field theories are not constants, but depend on the energy scale. The elementary charge also depends on the energy scale, whereby it increases with increasing energy. This means that at very high energies the interaction between charged particles is stronger. As a result, particle reactions due to the electromagnetic interaction are more likely at high energies. The probability that an electron-positron pair will be formed when two electrons collide, for example, increases with the energy of the collision.
The electroweak model states that both electromagnetism and the weak interaction are only effective interactions at low energies, which arise from spontaneous symmetry breaking by means of the Higgs mechanism . The electromagnetic interaction is described by the unbroken part of the symmetry, so that an electrical charge can be defined according to the Fabri-Picasso theorem . At higher energies, according to the model, two other interactions take the place of electromagnetism and the weak interaction and the electric charge is replaced by the weak hypercharge and the weak isospin . Accordingly, the electrical charge can in a certain sense be viewed as being composed of these two types of charge.
The symmetry of positive and negative charge is important for quantum field theory. The transformation that reverses all signs of the electric charges in a particle system is called C. Further important transformations in the following are P, the point reflection of space at the zero point, and T the reversal of the time direction. The CPT theorem , a fundamental statement about all quantum field theories, says that scattering processes take place in exactly the same way if all these three transformations are applied to the system. In general, this does not apply to the individual transformations, since there are parity-violating and CP-violating processes. However, electrodynamics is both P- and C-conserving.
Connection with other quantities
Electric charge as the foundation of electricity theory
Electrically charged bodies generate electric fields and are themselves influenced by such fields. The Coulomb force acts between the charges , the strength of which - compared to the gravitational force between the charge carriers - is very large. It has an attractive effect between a positive and a negative charge, and repulsive between two charges of the same name. The distance between the charges also plays a role in Coulomb's law . Electrostatics deals with static electric charges, charge distributions and the electric fields of charged bodies .
When bodies are charged, energy has to be expended to separate opposing charges that attract each other. After the charge separation, this energy is available as electrical field energy. The electrical voltage indicates how much work or energy is required to move an object with a certain electrical charge in the electrical field.
When electric charges move, one speaks of electric current . The movement of electrical charges leads to magnetic forces and electromagnetic fields ; this is described by Maxwell's equations and special relativity . Electrodynamics deals with moving charges in a more general form . The interaction of charged particles, which takes place by means of photons , is in turn the subject of quantum electrodynamics .
Charge density and electric field
This description of electrical interactions between elementary particles is practically only feasible for systems with a few particles. For many considerations, however, it is completely sufficient to work with spatially and temporally suitable averaged quantities, because the details that have not been taken into account are negligible for this macroscopic perspective. In this sense, the equations of electrodynamics were set up without having to know the submicroscopic structure of matter. The process of averaging does not formally change the basic equations of electrodynamics. Whether averaged or exact equations are meant depends on the context .
The description of the charge distribution takes place with the space charge density or the surface charge density . Based on the Coulomb field of a point charge , Gauss’s law results for the electric field generated by the space charge in a vacuum :
Where is the electric field constant . Gaussian law clearly means that electric field lines emanate from positive charges ( sources ) and end in negative charges ( sinks ).
In the theory of relativity, the electric field is combined with the magnetic field in the field strength tensor. The space charge density ( multiplied by the speed of light ) together with the electrical current density forms a four-vector .
Charge and electric current
When an electric current flows, then by a surface (for example, the cross-sectional area of an electrical conductor) is passed flowing charge amount (also current amount given) - based on the required for this period of time - as electrical current , respectively.
Simply put, the relationship between electric current and charge corresponds to the statement:
The amount of charge that was moved between and results from the integration of both sides:
For a current that is constant over time, the relationship between charge and current is simplified to:
Using this equation, it is also particularly easy to see that the unit Coulomb can be represented as . This relationship between the base units of amperes and seconds defines the coulomb in the International System of Units .
Because of the conservation of the charge, the amount of charge in a certain area of space changes only to the same extent as charges flow into or out of this area of space. The charge conservation thus corresponds to the continuity equation . The charge considered is equal to the volume integral of the charge density within the spatial area . The change in this charge over time is equal to the area integral of the current density over the closed surface of the volume ( read "edge of "), and is equal to the electrical current strength . The direction of flow out of the volume is defined as positive:
In a different notation, the continuity equation corresponds to the statement
where is the charge density and the current density.
Measurement of electrical charge
The amount of charge of 1 coulomb corresponds to about 6.24 · 10 18 elementary charges . In order to determine total charges, it is therefore usually not possible to simply count the charge carriers.
The amount of charge that has flown in or out can be determined indirectly by measuring the current strength: If a current of constant strength flows during the time , it transports the charge . In general, the charge that has flowed into or through a body is the integral of the electric current over time. If the discharge time is short compared to the oscillation period of a ballistic galvanometer , the charge can be read off directly as the amplitude of the oscillation initiated.
In principle, the value of a charge can also be determined by measuring the amount of force on a charged test body in an electric field of known field strength . The definition of the field strength provides the relationship
This method is subject to severe restrictions: the test body must be small, flexible and very well insulated electrically. Its charge must not noticeably influence the electric field, but this is difficult to check. Therefore, the charge should be low - but then the force is difficult to measure.
Another method does not have the disadvantages listed; it works even with quite large loads. The basis is the relationship between the capacitance of a capacitor and the electrical voltage :
A capacitor of known capacity is charged with the charge to be measured and its voltage is then measured. However, this measurement must be carried out with a high resistance , i.e. H. so that it takes only negligibly little of the stored charge from the capacitor. This is done with an electroscope or, better still, with an impedance converter . However, with this method, the capacity of the charge source must be known, as part of the charge remains there. The voltage-free measurement with an integrator (without input resistance also known as a charge amplifier ) avoids this problem.
literature
General
- Richard P. Feynman: Feynman lectures on physics. Oldenbourg, Munich / Vienna 2007, ISBN 978-3-486-58444-8 .
- Paul A. Tipler: Physics. 3rd corrected reprint of the 1st edition. 1994, Spektrum Akademischer Verlag, Heidelberg / Berlin, 2000, ISBN 3-86025-122-8 .
- Ludwig Bergmann, Clemens Schaefer: Electromagnetism. In: Textbook of Experimental Physics. Vol. 2, 9th edition. Walter de Gruyter, Berlin 2006, ISBN 978-3-11-018898-1 .
- Wolfgang Nolting: Electrodynamics. In: Basic Course Theoretical Physics. Vol. 3, 8th edition. Springer, Berlin 2007, ISBN 978-3-540-71251-0 .
About history
- Károly Simonyi : The cultural history of physics . Harri Deutsch, Thun, Frankfurt a. M. 1995, ISBN 3-8171-1379-X , pp. 320 ff .
- Hans-Peter Sang: History of Physics (Volume 1) . Klett, Stuttgart 1999, ISBN 3-12-770230-2 , p. 47 ff .
Web links
Individual evidence
- ↑ CODATA Recommended Values. National Institute of Standards and Technology, accessed June 3, 2019 . Numerical value of the elementary charge.
- ↑ a b c d e f g h i j k Károly Simonyi: cultural history of physics . Harri Deutsch, Thun, Frankfurt a. M. 1995, ISBN 3-8171-1379-X , pp. 320-330 .
- ↑ a b c d e f g Hans-Peter Sang: History of Physics (Volume 1) . Klett, Stuttgart 1999, ISBN 3-12-770230-2 , p. 48-56 .
- ↑ Ludwig Bergmann, Clemens Schaefer: Electricity. Walter de Gruyter, 1966. ISBN 978-3-11-144188-7 , p. 6.
- ^ Felix Auerbach: History of the development of modern physics. J. Springer, Berlin 1923. p. 263.
- ↑ Patent US307031 : Electrical Indicator. Published October 21, 1884 , inventor: TA Edison.
- ↑ Friedrich Herrmann: Two types of electrical charge. (PDF, 34 kB) Retrieved on February 15, 2010 (Prof. Herrmann explains why the manner of speaking of two types of summons has disadvantages.).
- ↑ John David Jackson (German translation and editing: Kurt Müller): Classic electrodynamics. 3rd, revised. Ed., De Gruyter, Berlin 2002, p. 317.
- ↑ Mattew D. Schwartz: Quantum Field Theory and the standard model . 1st edition. Cambridge University Press, Cambridge 2014, ISBN 978-1-107-03473-0 , pp. 634 (English).