Muon
|
Muon (µ - ) |
|
|---|---|
| classification | |
|
Elementary particle fermion lepton |
|
| properties | |
| electric charge | −1 e (-1.602 176 634 · 10 −19 C ) |
| Dimensions | 0.113 428 9259 (25) u 1.883 531 627 (42) · 10 −28 kg 206.768 2830 (46) m e |
| Resting energy | 105.658 3755 (23) MeV |
| Compton wavelength | 1.173 444 110 (26) · 10 −14 m |
| magnetic moment | −4,490 448 30 (10) · 10 −26 J / T |
| g factor | −2.002 331 8418 (13) |
| Spin | 1/2 |
| average lifespan | 2.196 9811 (22) · 10 −6 s |
| Interactions |
weak electromagnetic gravitation |
The muon (English: muon ) is an elementary particle that resembles the electron in many properties . Like the electron, it has a negative elementary charge and a spin of 1 ⁄ 2 . Muon and electron are subject to the electroweak , but not the strong interaction . The muon, however, has a mass around 200 times greater . Furthermore, in contrast to the electron, it decays spontaneously with an average lifetime of only about 2.2 microseconds. The formula symbol of the muon is . The antiparticle of the muon is the positive muon or antimuon . Like the positron, it is simply positively charged.
Muons were discovered by Carl D. Anderson and Seth Neddermeyer studying cosmic rays in 1936 and independently detected by J. Curry Street and EC Stevenson in 1937 (both groups published in the same Physical Review 1937 issue). Since a center of gravity energy of approx. 106 MeV is necessary for their production , they are not created either by radioactive decay or by nuclear weapon explosions. Particle accelerators are required for artificial production .
As leptons , electron and muon are related particles in the Standard Model . The electron belongs to the first and the muon to the second of the three lepton families. The corresponding particle of the third family is the τ-lepton, discovered in 1975 .
The muon used to be called the mu-meson . “Meson” (Greek, about the mean ) - even earlier also “mesotron” - meant “medium-weight” particle at that time, namely with a mass between electron and proton . In the 1960s, however, the designation meson was restricted to particles with strong interaction, to which the muon as a lepton does not belong.
Cosmic rays
Muons are a major component of secondary cosmic rays. This is caused by reactions of the actual cosmic radiation (especially protons coming from space) with atomic nuclei in the upper atmosphere . Most muons are formed in the outer atmosphere: 90 percent of all muons produced in the entire atmosphere have already formed at a height of about 10 km. The reactions of the primary radiation initially produce pions and, to a lesser extent, kaons ; when they decay due to the weak interaction , muons and muon neutrinos are created. At sea level, the particle flux density of these “cosmic” muons is around 100 per square meter and second, the measured ratio is around 1.27.
In 2016, at the Auger Observatory , the indications of a consistent model of high-energy physics inexplicable muon surplus in cosmic radiation, which either points to new physics (for primary energies of cosmic radiation of 10 19 eV in the upper atmosphere, corresponds to the center of gravity energies of Collision with air molecules of 110 to 170 TeV and thus ten times the value attainable with the LHC) or for gaps in the understanding of hadronic collision processes.
Detection of muons
Muons, with their mostly high kinetic energy, create long ionization tracks in matter through many successive collisions , which can be used for detection. Since they usually move at almost the speed of light , they generate z. B. Cherenkov radiation in water .
Also scintillators and semiconductor detectors are sensitive to muons. The muons from secondary cosmic rays, for example, often make up the main part of the background effect in gamma spectrometers , because their high energy allows them to penetrate several meters of lead and can therefore hardly be shielded in the laboratory .
In experiments in particle physics, muons are distinguished from other particles by various techniques:
- By measuring longer tracks, the place of origin and the direction of movement of the muons can be determined.
- By measuring traces in magnetic fields, the ratio of charge to momentum can be determined. Together with a speed measurement, conclusions can be drawn about the mass of the particle.
- The high permeability for matter can also be used for identification.
Decay
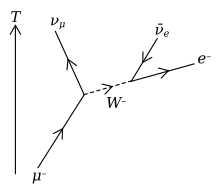
According to the Feynman diagram shown on the right, the free muon decays into a muon neutrino , an electron antineutrino and an electron
- .
An electron-positron pair is rarely also generated:
The generation of gamma radiation ( photons ) is also possible:
The decay of the antimuon is obtained by replacing all particles with the respective antiparticle
- .
According to the Standard Model, the decay of the muon is mediated by a W boson (see also boson ).
The experimentally determined mean lifetime of the positive muon is 2.196 981 1 (2 2) µs. The negative muon has an additional decay channel in matter : it can form a muonic atom with an atomic nucleus and then be absorbed by the nucleus in accordance with the K capture of an electron. A proton becomes a neutron and a muon neutrino is emitted. That is why the experimentally determinable mean lifetime of the negative muon is shorter in matter. In a vacuum, without this additional decay channel, the measured lifetimes of positive and negative muon agree with an accuracy of 0.1 percent.
Time dilation
The time dilation of moving particles enables the muons that arise in the upper atmosphere to reach the earth's surface despite their short half-life of 1.523 µs (see secondary cosmic radiation ). Without this relativistic effect, even if moving at the speed of light, half of all muons would have decayed again after around 450 m.
The lifespan of muons of different energies was first measured in 1940 by Bruno Rossi and David B. Hall . A Wien filter limited the measurement to muons at 99.5 percent of the speed of light. The comparison of the measured numbers of particles made it possible to determine the half-life of these fast muons; at 13 μs it was about nine times longer than for muons at rest. Fast muons therefore decay more slowly than muons at rest. In 1963, Frisch and Smith carried out a similar experiment with greater accuracy.
The considerable flow of fast muons from the secondary cosmic radiation while still on the ground represents a disturbing background when measuring weak radiation sources. It is one of the reasons for such measurements in underground laboratories in earlier mines and the like. (such as the Gran Sasso Laboratory ).
Decay channels forbidden in the standard model
Certain neutrino-free decay channels of the muon are kinematically possible, but forbidden in the standard model (i.e. also without neutrino oscillations ) and have not yet been observed. This is expressed by the conservation laws of the lepton flavors (conservation of the lepton family numbers in each interaction vertex ), from which it also follows that the muon is not an excited state of the electron. Examples of such decays that would change the lepton flavor are
and
- .
The observation of such a decay would be an indication of a new physics beyond the Standard Model (New Physics). In the last 50 years the upper limit for the branching ratios of such decays has been continuously improved in numerous experiments . The current limit value (2020) for decay was determined in the MEG experiment to be 4.2 · 10 −13 . The Mu3e experiment plans to improve the limit value for the other decays from the current 10 −12 to 10 −16 .
Magnetic anomaly of the muon
Muons are particularly suitable for studying fundamental forces in physics at the highest level of precision. As far as we know today, like all leptons they are point-shaped. This allows their properties to be calculated very precisely within the framework of quantum electrodynamics . The influence of forces other than the electromagnetic force is small, but can be observed through virtual particles surrounding the muon. This leads to a deviation in the magnetic properties of the muon.
The magnetic anomaly of the muon is also called the g − 2 value, where g is the Landé factor . It is the deviation of the value determined by quantum corrections from the value obtained by solving the Dirac equation ( ). The standard model of elementary particle physics predicts for these corrections:
A precision measurement of this magnetic anomaly was made at Brookhaven National Laboratory by a worldwide collaboration around the year 2000. Should there be other particles than those currently known to particle physics and should these not have too large masses, then they should make themselves noticeable in the magnetic anomaly of the muon. The determined value of
was 2.2-2.7 standard deviations above the theoretical prediction, which was not a significant deviation from the theoretical prediction.
At the beginning of April 2021, the first results of the Muon g-2 experiment at the Fermilab were published, with higher accuracy and a value of
confirmed this slight deviation. The significance of at least 5 σ usually required in particle physics has not yet been achieved, but the probability that the deviation resulted purely by chance is in the order of magnitude of 1: 40,000.
The combined result of Brookhaven and Fermilab therefore deviates
from the theoretically predicted result, which, with 4.2 standard deviations, corresponds to a probability of chance of about 1: 100,000. Thus, evidence suggests an unknown fundamental interaction ( Fifth Force ).
Muonic atoms
Like electrons, the negatively charged muons can be bound to atomic nuclei . However, the associated Bohr radius of the “muon orbit” around the atomic nucleus is smaller by the ratio of the mass of the muon to the electron. This means that muons are much more tightly bound to the nucleus than electrons. Moving in the nucleus is around 7 orders of magnitude more likely than electrons.
Especially with heavy atomic nuclei and with muons that occupy the 1s orbital after capture , the probability of a muon being located within the atomic nucleus increases to significant values. When the muon is then absorbed by the nucleus, inverse beta decay occurs and a proton is converted into a neutron . This also creates a neutrino and possibly some gamma quanta. The newly created atomic nucleus is often radioactive . If this subsequently goes through a normal beta decay, the original atomic nucleus is created again.
Due to the additional reaction probability a bound muon has a significantly shorter service life, in copper z. For example, about 0.163 microseconds . This is z. B. used in muon spin analysis.
Since the bound muon shields part of the nuclear charge, the energy levels of the bound electrons shift. Furthermore, the Pauli principle applies to electrons and leptons with one another, but not between different types of particles. In a muonic atom, in addition to two electrons in the 1s state, one or two muons in the 1s state can also exist.
The only additional decay path open to the bound muon - besides all the decay channels of the free muon - is the core capture. Core capture is the dominant process for heavy kernels. Further disintegration possibilities are currently being sought, e.g. For example, the so-called muon-electron conversion . Since this process is not possible in the standard model of particle physics, it would be a clear sign of so-called new physics.
Antimuons, on the other hand, with their positive charge, like protons or positrons, can themselves capture an electron. This results in a exotic atom , the muonium is called.
Measurement of the proton radius
Measuring the Lamb shift of normal hydrogen and muonic hydrogen is one way of determining the proton radius. It differs due to the different distances between the proton and the corresponding lepton and thus enables the measurement of deviations in the Coulomb potential on very small distance scales by measuring the energy differences between 2s and 2p states through absorption of laser radiation. According to QED, the shift observed at the Paul Scherrer Institute in 2010 would be caused by a proton radius of (841.84 ± 0.67) · 10 −18 m. The value does not agree with the value (876.8 ± 6.9) · 10 −18 m from scattering experiments (one of the unsolved problems in physics ). In 2016, the smaller values of the proton radius were confirmed by the same measurements on the deuteron, which were also carried out at the Paul Scherrer Institute. In 2017, measurements of a deviation were confirmed by laser spectroscopy on ordinary hydrogen.
Muon Catalyzed Fusion
If a muon is captured by a deuterium - or a deuterium- tritium - molecule (D 2 or DT), a positive muonic molecule ion is created because the relatively large binding energy of the muon releases the two electrons of the molecule. In this muonic molecular ion, the two atomic nuclei are about 200 times closer to each other than in an electronic molecule. The possible by the tunnel effect the fusion of the two cores. The very high energy released by the fusion (with D + D around 3 MeV, with D + T 14 MeV) also releases the muon again and, depending on the environmental conditions, it can catalyze many more (around 10 2 ) individual fusions during its lifetime .
In order to be able to generate useful energy with this muonically catalyzed nuclear fusion, the individual fusions that take place up to the decay of the muon (lifespan 2.2 µs ) must release more energy than was required to generate the muon. Current particle accelerator facilities are many orders of magnitude away from this.
The muon-catalyzed fusion is also known as cold fusion . It was originally proposed by Andrei Sakharov .
To date, no experimental or theoretical results on "cold fusion" have been recognized that would undoubtedly make a muon-catalyzed fusion possible for energy generation .
Applications
Cosmic rays contain muons with an energy of several GeV. Thanks to their high kinetic energy , they can penetrate rock several kilometers thick before they are slowed down to speeds well below the speed of light and then disintegrate. Therefore, they can be used in muon tomography to x-ray larger objects. For this purpose, the muons of cosmic rays are used and their scattered radiation is measured and evaluated tomographically .
The Chephren pyramid was examined by Luis Walter Alvarez in the 1960s .
In 2009 the method was applied to the Iō-dake volcano ( Japanese硫黄 岳) on the island of Iojima ( Kikai Caldera , Ōsumi Islands ). This made it possible to determine the density distribution of the volcano.
In the fall of 2017, researchers announced the discovery of a cavity at least 30 m long in the Great Pyramid of Cheops above the Great Gallery through muon tomography .
Trivia
The muon, discovered in 1936, was initially mistaken for the exchange particle of nuclear power postulated by Hideki Yukawa in 1935 , which is now known as a pion . This oversight caused a. from the similar mass of the two particles. The confusion was cleared up in 1947 by the discovery of the pion.
Web links
- What are muons? from the alpha-Centauri television series(approx. 15 minutes). First broadcast on Apr 14, 2004.
- Integrated Infrastructure Initiative for Neutron Scattering and Muon Spectroscopy (NMI3). European consortium with 18 partner organizations from 12 countries, all important institutions in the fields of neutron scattering and muon spectroscopy. (English).
Individual evidence
- ↑ Unless otherwise stated, the information on the particle properties of the info box is taken from the publication of the CODATA Task Group on Fundamental Constants : CODATA Recommended Values. National Institute of Standards and Technology, accessed July 4, 2019 . The figures in brackets denote the uncertainty in the last digits of the value; this uncertainty is given as the estimated standard deviation of the specified numerical value from the actual value.
- ↑ C. Patrignani et al. ( Particle Data Group ): 2017 Review of Particle Physics. In: Chin. Phys. C . Vol. 40, 2016, 100001 and 2017 Review of Particle Physics. Particle Data Group, accessed July 4, 2019 .
- ↑ Páll Theodorsson: Measurement of Weak Radioactivity . World Scientific, 1996, ISBN 978-981-02-2315-1 , pp. 85 ( books.google.com [accessed April 22, 2012]).
- ↑ C. Grupen: Astroparticle Physics. Springer 2005, ISBN 3-540-25312-2 , p. 149.
- ↑ Dirk Eidemüller: Excess muons in cosmic showers. In: Pro-Physik.de. November 7, 2016.
- ↑ A. Aab et al .: Testing Hadronic Interactions at Ultrahigh Energies with Air Showers Measured by the Pierre Auger Observatory. In: Phys. Rev. Lett. 117, 192001 (2016).
- ↑ SL Meyer, EW Anderson, E. Bleser, IM Lederman, JL Rosen, J. Rothberg, IT Wang: Precision Lifetime Measurements on Positive and Negative Muons . In: Physical Review . tape 132 , no. 6 , 1963, pp. 2693-2698 , doi : 10.1103 / PhysRev.132.2693 .
- ^ Roman Sexl, Herbert K. Schmidt: Space-Time-Relativity . Vieweg, Braunschweig 1979, ISBN 3-528-17236-3 , pp. 82-85 .
- ^ B. Rossi, DB Hall: Variation of the Rate of Decay of Mesotrons with Momentum . In: Physical Review . 59, No. 3, 1941, pp. 223-228. doi : 10.1103 / PhysRev.59.223 .
- ^ B. Rossi, K. Greisen, JC Stearns, DK Froman, PG Koontz: Further Measurements of the Mesotron Lifetime . In: Physical Review . 61, No. 11-12, 1942, pp. 675-679. doi : 10.1103 / PhysRev.61.675 .
- ↑ B. Rossi, N. Nereson: Experimental Determination of the Disintegration Curve of Mesotrons . In: Physical Review . 62, No. 9-10, 1942, pp. 417-422. doi : 10.1103 / PhysRev.62.417 .
- ↑ B. Rossi, N. Nereson: Further Measurements on the disintegration of Curve Mesotrons . In: Physical Review . 64, No. 7-8, 1943, pp. 199-201. doi : 10.1103 / PhysRev.64.199 .
- ↑ David H. Frisch, James H. Smith: Measurement of the Relativistic Time Dilation Using μ-Mesons . In: American Journal of Physics . 31, No. 5, 1963, pp. 342-355. doi : 10.1119 / 1.1969508 .
- ↑ AM Baldini, Y. Bao, E. Baracchini, C. Bemporad, F. Berg: Search for the lepton flavor violating decay $$ \ mu ^ + \ rightarrow \ mathrm {e} ^ + \ gamma $$ μ + → e + γ with the full dataset of the MEG experiment: MEG Collaboration . In: The European Physical Journal C . tape 76 , no. 8 , August 2016, ISSN 1434-6044 , p. 434 , doi : 10.1140 / epjc / s10052-016-4271-x ( springer.com [accessed February 6, 2020]).
- ↑ T. Aoyama et al .: The anomalous magnetic moment of the muon in the Standard Model . 2020, arxiv : 2006.04822 .
- ↑ The E821 Muon (g-2) Home Page. Ernst Sichtermann, accessed on June 8, 2009 (English).
- ^ The Muon g − 2 Collaboration: Final Report of the Muon E821 Anomalous Magnetic Moment Measurement at BNL . In: Phys. Rev. D . tape 73 , no. 7 , April 1, 2006.
- ^ Muon g − 2 Collaboration: Measurement of the Positive Muon Anomalous Magnetic Moment to 0.46 ppm . In: Physical Review Letters . tape 126 , no. 14 , April 7, 2021, p. 141801 , doi : 10.1103 / PhysRevLett.126.141801 ( aps.org [accessed April 8, 2021]).
- ↑ First results from Fermilab's Muon g − 2 experiment strengthen evidence of new physics , press release from Brookhaven National Laboratory, April 7, 2021
- ↑ Darling, I've shrunk the deuteron! In: Pro-Physik.de. August 12, 2016.
- ↑ R. Pohl et al.: Laser spectroscopy of muonic deuterium. In: Science. Volume 353, 2016, pp. 669-673.
- ↑ WH Breunlich: muon Catalyzed Fusion. Nuclear Physics A. Vol. 508 (1990) pp. 3-15.
- ↑ Sources of Energy. The cold fusion - wish or reality? November 20, 2014 ( Spektrum.de [accessed April 12, 2018]).
- ↑ Bart Simon: Undead Science: Science Studies and the Afterlife of Cold Fusion . 1st edition. Rutgers University Press, ISBN 978-0-8135-3153-3 .
- ↑ Look into the throat . In: Image of Science . No. 10 , 2009, p. 61 f . ( Wissenschaft.de ).
- ↑ Hiroyuki KM Tanaka, Tomohisa Uchida, Manobu Tanaka, Hiroshi Shinohara, Hideaki Taira: Cosmic ‐ ray muon imaging of magma in a conduit: Degassing process of Satsuma ‐ Iwojima Volcano, Japan . In: Geophysical Research Letters . tape 36 , no. 1 , 2009, doi : 10.1029 / 2008GL036451 .
- ↑ Discovery of a big void in Khufu's Pyramid by observation of cosmic-ray muons . Authors: Morishima, K. et al., From: nature.com November 2, 2017, accessed November 2, 2017.
















