Compton effect
| Feynman diagrams |
|---|
s channel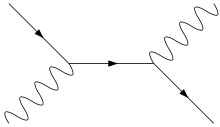
|
t channel
|
The Compton effect is the increase in the wavelength of a photon when it is scattered by a particle . The Compton effect on electrons was observed for the first time. This Compton scattering (after Arthur Holly Compton , who received the Nobel Prize for Physics for this in 1927 ) is an important ionization process and the dominant process of interaction of high-energy radiation with matter for photon energies between about 100 keV and 10 MeV.
history
Until the discovery of the Compton effect, the photo effect was the only finding that light behaves not only like a wave, but also like a stream of particles (see also wave-particle dualism ).
When Arthur Compton investigated the scattering of high-energy X-rays on graphite in 1922 , he made two observations: On the one hand, the scattering angle distribution in the forward and backward directions was not the same and, on the other hand, the wavelength of the scattered radiation was greater than that of the incident radiation. Both observations were incompatible with the idea that an electromagnetic wave would be scattered by free electrons ( Thomson scattering ) or by bound electrons ( Rayleigh scattering ), because then the electrons would oscillate with the frequency of the incident wave and emit a wave with an unchanged frequency .
Instead, Compton's measurements showed that the wavelength of the scattered radiation behaves, depending on the scattering angle, like a collision between particles, the photon and the electron (for derivation see below). Compton thus confirmed the particle character of light - or the wave character of electrons, because if electrons are treated as matter waves and light as electromagnetic waves, the Compton effect results, as in the above Feynman graphs .
Compton wavelength
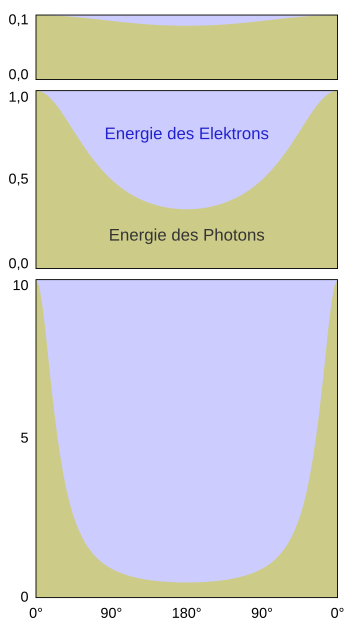
When a (quasi) free, resting electron collides, it takes over part of the energy of the photon, the energy of which is reduced - it is an elastic collision . The greater its output energy, the more completely the energy can be transferred, see figures on the right. The scattering angle is the angle by which the direction of movement of the photon changes. In the case of a “grazing shot” with a deflection , the photon retains almost all of its energy, in a “head-on collision” the photon is scattered back and emits the maximum energy that can be transmitted.
Due to the loss of energy, the wavelength of the photon increases. It is noteworthy that this increase only depends on the angle and not on the original photon energy:
The Compton wavelength is a characteristic quantity for a particle with mass. It indicates the increase in the wavelength of the photon scattered at right angles from it.
The Compton wavelength of a particle of mass is
where is Planck 's constant and the speed of light in vacuum .
Frequently (especially in elementary particle physics) the reduced Compton wavelength is also used with the reduced Planck quantum and also referred to as the Compton wavelength without the addition reduced . In this form, the Compton wavelength appears as a parameter in the Klein-Gordon equation .
Compton wavelengths of electron, proton and neutron
The Compton wavelengths of electrons, protons and neutrons are thus, unlike their De Broglie wavelengths , independent of their speed; According to the current measurement accuracy, their values are:
The reduced Compton wavelength of the electron is 386 fm , that of the proton and neutron 0.210 fm.
The very small changes in wavelength are the reason why the Compton effect can only be observed with very short-wave radiation , in the range of X-rays and gamma rays . At long wavelengths their relative increase is too small, the scattering seems to take place without any loss of energy, one then speaks of Thomson scattering .
Scattering cross-section
The angle-dependent cross section for Compton scattering is given (in the approximation of free, resting electrons) by the Klein-Nishina formula . With Compton scattering in matter, an electron is knocked out of the atomic shell . In this case, these formulas only apply approximately. The influence of the momentum of the bound electron on the energy of the scattered photon is called Doppler broadening . It is the projection of the momentum distribution of the scattering electrons onto the direction of the momentum transfer during the scattering. It is particularly pronounced at low photon energies, large scattering angles and atoms with a high atomic number .
If photons are scattered on objects other than electrons, for example on a proton, the mass must be adjusted accordingly in the above equations , which would change the Compton wavelength and cross section.
Inverse Compton effect
In the inverse Compton effect , a high-energy electron (or another charged particle, such as a proton) scatters on a low-energy photon and transfers energy to the photon. The inverse Compton effect occurs in particle accelerators and can be observed in astrophysics with outflows in the corons of accretion disks of active galaxy nuclei and with supernovae (see also Sunjajew-Seldowitsch effect ). Inverse Compton scattering at the background radiation limits the maximum energy of protons in cosmic rays (see also GZK cutoff ).
Applications
Since it is very difficult to focus gamma radiation using lenses , the Compton effect plays an important role in imaging using gamma rays in the energy range from a few hundred keV to a few tens of MeV . In so-called Compton telescopes (also called Compton cameras) one measures the energy and direction of the scattered photon as well as the energy and (sometimes) the direction of the electron. In this way, the energy, direction of origin and, under certain circumstances, the polarization of the incident photon can be determined. In reality, however, this is made very difficult by measurement uncertainties and unmeasured quantities such as the direction of the electron, so that complex event and image reconstruction methods have to be used.
Probably the best known Compton telescope was COMPTEL, which was the first telescope to explore the starry sky in the energy range between 0.75 and 30 MeV on board NASA's CGRO satellite from 1991 to 2000. COMPTEL's successes include a. the creation of the first sky maps in this energy range, the research into nucleosynthesis z. B. of radioactive 26 Al (massive stars and supernovae ) and 44 Ti as well as advances in the study of pulsars , active galaxies (AGNs) etc.
Compton cameras could in the future provide better spatial resolution in the medical field compared to the scintigraphy gamma cameras used today (2019), i.e. localize tumors and metastases more precisely. In the future, Compton cameras could be used in nuclear technology. B. nuclear facilities or nuclear waste are monitored.
For security controls at airports, scanner devices have been developed that use the Compton backscatter of X-rays on surfaces. These are currently being tested in the USA.
The inverse Compton effect is used to generate monochromatic, linearly polarized gamma radiation by backscattering laser photons from high-energy electrons.
Compton continuum and Compton edge
From the formulas derived below, it is easy to calculate an expression for the angle-dependent energy of the photon and the kinetic energy of the electron according to the scattering ( Klein-Nishina formula ):
- Photon:
- Electron:
If many photons of the energy according to Compton are scattered (for example in a scintillator or other detector), a characteristic energy spectrum of the scattered electrons results, as shown in the adjacent graphic. The energy transferred to the electrons is a continuous function of the scattering angle ( Compton continuum ), but has a sharp upper bound. This so-called Compton edge arises because the scattered photons transfer the greatest possible energy to the electrons at = 180 °. Thus the edge is included in the spectrum
- .
In addition, a “ photopeak ” or “full energy peak” is obtained in the energy spectrum , a spectral line in the energy . It comes from detection events in which the entire energy of the photon was deposited in the detector, for example through the photo effect . From the above formula it can be seen that the Compton edge belonging to a photopeak is at
to the left of this peak.
The figure on the right shows a spectrum recorded with a germanium detector (see gamma spectroscopy ) . The photopeak of the gamma radiation is found at around 4.4 MeV, which originates from inelastic neutron scattering on 12 C atomic nuclei (the line is Doppler broadened by the recoil movement of the carbon nuclei ). From the gamma energy 4.4 MeV it follows with the above equation that the associated Compton edge must be around 4.2 MeV, where it can also be easily seen in the figure. To the left of it shows the associated continuum with peaks of other origin on it.
Derivation of the Compton formula
A free electron is always assumed for the different derivations. If the electron is bound in an atom, the binding energy must be subtracted from the kinetic energy of the electron after the collision.
Resting electron
In the following we calculate the Compton formula by assuming the particle to be initially at rest. During the scattering, the photon transfers part of its energy to the electron , so that the two particles move apart in different directions after the scattering.
First, we consider which energy and which momentum the respective particles carry before and after the scattering ( stands for the frequency and the scattering angle):
Energy of ... Impulse of ... Electrons before Photons before Photons before Electrons before Electrons afterwards Photons afterwards Photons afterwards Electrons afterwards
The two particles must satisfy the law of conservation of energy and momentum before and after the scattering .
Conservation of energy law Momentum conservation law
In the special theory of relativity, the energy and momentum of a particle are related to each other via the energy-momentum relationship . Since the particles move on the sides of a triangle that correspond to their respective momentum, the spatial momentum is related via the cosine law . The following applies:
Energy-momentum relationship Cosine law
After inserting the expressions for and into the energy-momentum relationship and combining the terms, this follows
In the last transformation, the relationship between wavelength and frequency was used .
Any reference system
While the Compton effect can easily be calculated trigonometrically in the case of an electron at rest, the situation is more difficult in any reference system. In this case, the electron moves before the collision with the speed , carrying the total energy and momentum ,
with and .
In order to calculate the Compton effect in the case under consideration, we use the four-vector formalism.
The four impulses that the particles involved have before and after the scattering process are
Electron before Photon before Electron after Photon after
Here denotes a unit vector which points in the direction of movement of the photon.
From the energy-momentum relation follows and . The following applies to the mixed products
Here designated
- the angle between the directions of movement of the electron and the photon before the scattering,
- the angle between the directions of movement of electron before scattering and photon after scattering and
- the angle between the directions of movement of the photon before the scattering and the photon after the scattering.
If a photon is scattered by an electron, the conservation of energy and momentum must be fulfilled. Since the energy is proportional to the zero component of the four-pulse and the remaining components represent the pulse, it follows
- .
After inserting the scalar products and forming follows
Depending on the angle of incidence and kinetic energy, the electron can transfer a certain amount of energy to the photon (inverse Compton scattering). In the rest system of the electron, the speed of the electron before the collision was zero. So is
- and ,
with which the already known formula
results.
literature
- Hanno Krieger: Fundamentals of radiation physics and radiation protection . 4th edition. Springer, 2012, ISBN 978-3-8348-1815-7 .
- Jörn Bleck-Neuhaus: Elementary Particles . Springer, 2013, ISBN 978-3-642-32578-6 .
- Peter Schmüser: Feynman graphs and gauge theories for experimental physicists . Springer, 1994, ISBN 3-540-58486-2 .
Web links
- COMPTON effect. LEIFI Physics, accessed on March 23, 2017 (explanation and animation).
Individual evidence
- ^ Arthur H. Compton: Secondary Rediations produced by X-rays and some of their applications to physical problems . In: Bulletin of the National Research Council . tape 20 , 1922, pp. 10 . ; Reprinted in: Arthur Holly Compton, Robert S. Shankland: Scientific papers of Arthur Holly Compton . University of Chicago Press, 1973, ISBN 0-226-11430-9 ( limited preview in Google Book Search).
- ↑ Arthur H. Compton: A Quantum Theory of the Scattering of X-rays by Light Elements . In: Physical Review . tape 21 , no. 5 , 1923, pp. 483-502 , doi : 10.1103 / PhysRev.21.483 .
- ↑ For example Bjoerken / Drell Relativistic Quantum Mechanics , McGraw Hill 1964, Peskin, Schröder Introduction to Quantum Field Theory , West View Press 2007. But not in the Particle Data Group, PDG, Physical Constants
- ↑ CODATA Recommended Values. National Institute of Standards and Technology, accessed July 8, 2019 . Value for the Compton wavelength of the electron. The numbers in brackets denote the uncertainty in the last digits of the value; this uncertainty is given as the estimated standard deviation of the specified numerical value from the actual value.
- ↑ CODATA Recommended Values. National Institute of Standards and Technology, accessed July 8, 2019 . Value for the Compton wavelength of the proton. The numbers in brackets denote the uncertainty in the last digits of the value; this uncertainty is given as the estimated standard deviation of the specified numerical value from the actual value.
- ↑ CODATA Recommended Values. National Institute of Standards and Technology, accessed July 8, 2019 . Value for the Compton wavelength of the neutron. The numbers in brackets denote the uncertainty in the last digits of the value; this uncertainty is given as the estimated standard deviation of the specified numerical value from the actual value.
- ↑ Peter Schmüser, p. 69 .


































































