polarization

The polarization of a transverse wave describes the direction of its oscillation . If this direction changes quickly and in a disorderly manner, one speaks of an unpolarized wave. The degree of polarization indicates the ordered proportion. In the case of waves oscillating in the direction of propagation , the longitudinal waves , there is no polarization in the actual sense or one speaks of longitudinal polarization.
Components that polarize unpolarized light or split or suppress polarized light depending on the type and direction of polarization are called polarizers .

Types of polarization
- linear polarization : the direction of the oscillation is constant. The deflection from the rest position (in the case of the mechanical wave a displacement perpendicular to the direction of propagation) periodically changes its magnitude and sign . The direction in relation to a certain plane can be specified as an angle (common with seismic waves ) or as a proportion of the two components parallel or perpendicular . For electromagnetic waves, see the following chapter.
- Circular polarization (called rotating polarization in the 19th century ): The amount of deflection is constant (apart from modulation ), its direction changes within the plane perpendicular to the wave vector (the xy plane in the picture) with constant angular velocity. For the direction of rotation see helicity . However, in the literature, especially the older ones, it is often defined as right-circular polarization as clockwise rotation when looking against the direction of propagation (corresponding to a left-hand screw). Abbreviations: RHCP and LHCP for right- or left-handed polarization ( Right Hand Circular Polarization and Left Hand Circular Polarization ).
- elliptical polarization is a hybrid form. The deflection describes an ellipse.
Mathematical description
- Composition of a linear, circular or elliptically polarized wave (black) from linearly polarized components (red and blue)
Mathematically, the possible polarizations of waves of the same wavelength and frequency are understood as elements of a 2-dimensional vector space. What is physically a superposition of states corresponds to a linear combination of vectors on the mathematical side. Since amplitude ( ) and phase ( ) must be taken into account when superimposing, complex numbers ( ) are used as scalar factors : The polarization states of light therefore form a vector space over the body of complex numbers. As a basis (with which one can represent each vector) the two circularly polarized states (left or right rotating) are often used, on the one hand, and any two linearly polarized states with mutually perpendicular oscillation planes on the other. Each base can be expressed by the other. A circularly polarized state is a superposition of two linearly polarized states with mutually perpendicular oscillation planes, but a linearly polarized state is also a superposition of the two circularly polarized ones. The position of the oscillation plane is determined by the phase difference between the circularly polarized states. If base states with different amplitudes or a circularly with a linearly polarized state are superimposed, then elliptically polarized light is obtained.
Photons are bosons and can have spin components +1 or −1, which corresponds to the two possibilities of circular polarization (the component zero cannot occur because the photon moves at the speed of light, see helicity ). The spin axes point depending on the helicity in the direction of propagation or against it. Linear polarization results from the linear superposition of the two circularly polarized states with the same amplitude, the photons then have the value zero for the expected value of the angular momentum.
When describing superimpositions, the amplitude ratio and the phase position must always be specified.
- If two circularly polarized waves, one clockwise and one counterclockwise, are superimposed, the following polarizations result:
- With the same intensities and variable phase difference, the resulting polarization is linear and the direction depends on the phase position of the base polarizations.
- In any other case, elliptical polarization results.
- If two linearly polarized waves, whose polarization directions are perpendicular to each other, are superimposed, the following polarizations result:
- With a vanishing phase difference (or a phase difference which corresponds to a multiple of ) and different or equal amplitudes, the resulting polarization is linear and the direction depends on the amplitude ratio.
- With a phase difference of and equal amplitudes, the output polarization is circular.
- In any other case the resulting polarization is elliptical.
If the absolute intensity and the degree of polarization are also of interest, a total of four items of information are necessary, as a four-dimensional real - valued Stokes vector or as a two - dimensional complex - valued Jones vector . If one is only interested in the polarization and not in the absolute intensity, the Poincaré sphere is often used to represent the polarization states.
As an alternative, quasi-monochromatic light can also be described by the coherence matrix. The description of the effect of a polarization-changing optical element is then carried out by multiplication with a corresponding Müller matrix or a Jones matrix .
Polarization of electromagnetic waves
Unpolarized and polarized light in nature
The form of electromagnetic radiation predominantly observed on earth and in the universe is thermal radiation and thus initially unpolarized, that is, the individual waves are statistically distributed in their properties; it is therefore a matter of the superposition of a large number of individual waves with the most varied of positions of the oscillation plane and relative phase. Partly polarized light is produced from this through reflection and / or scattering, in which part of the individual waves has the same properties with regard to their polarization and appears as a polarization pattern .
Oblique reflection at interfaces, e.g. B. on a water surface, light partially separates according to its polarization direction. The part polarized in the reflection plane penetrates rather, the part perpendicular to it is more likely to be reflected. For the quantitative dependence on the angle of incidence see Fresnel's formulas .
The blue light of the sky is sunlight scattered by molecules and statistical fluctuations in density in the air. The air is electrically polarized by the incident wave in random directions perpendicular to the direction of incidence . Scattered light in the directions of this oscillation plane (scattering angle 90 °) oscillates in this plane, so it is completely polarized. For the dependence on the scattering angle, see Rayleigh scattering . However, the light from the sky is not completely polarized due to multiple scattering and scattering on particles.
Perception of polarized light
Many insects can distinguish linearly polarized light according to its polarization direction and use this effect to orientate themselves. Karl von Frisch researched this for the honey bee .
Also mantis shrimp , the water bug Notonecta glauca , greater mouse-eared ( Myotis myotis ) and desert ants are capable of doing, as well as people, but with very low contrast ( Haidinger's Brush phenomenon).
Names of the subgroups of the types of polarization
Electromagnetic radiation ( light , radio waves , etc.) is a transverse wave with right angles between the wave vector pointing in the direction of propagation and the vectors of the electric and magnetic fields, respectively . It is arbitrary whether the direction of polarization is the direction of oscillation of the electric or the magnetic field. However, and mean different directions of oscillation for the wave. These are perpendicular to each other. From the time when light was still explained as a mechanical oscillation of the hypothetical ether, a definition for the designations of the two polarization directions comes from, which later turned out to be the oscillation direction of the magnetic field vector. Since most of the interactions between electromagnetic radiation and matter are electrical in nature, the direction of polarization is mostly related to the electrical field vector today.
If the wave is refracted, reflected or scattered, the reference plane for the terms parallel and perpendicular is the plane in which the incoming and outgoing waves lie. In the case of radio waves, the earth's surface represents the “reference plane” and the components are usually called horizontal and vertical .
In addition to parallel and perpendicular polarized waves, other terms are used to describe the reflection. One speaks of TM-polarized light when the direction of the magnetic field is perpendicular to the plane (" plane of incidence ") spanned by the incidence vector and surface normals (TM = transversely magnetic; one also speaks of parallel , p or π polarized light Light , since the electric field perpendicular to the magnetic field in isotropic materials lies in the plane of incidence), and of TE-polarized light when the electric field is perpendicular to the plane of incidence (TE = transversal electric; one speaks here of perpendicular , s- or σ-polarized light ). In the direction of the Brewster's angle , TM-polarized light is refracted more intensely into the medium instead of being reflected, that is, the light emerging at the Brewster's angle is always TE-polarized even for unpolarized incident light. Both terms are only defined in connection with the reflective surface.
In the case of circular or elliptically polarized light, a distinction is made with regard to the direction of rotation of the E or H vector in relation to the direction of propagation. One speaks here of left- or right-rotating polarized light (for the naming conventions see above).
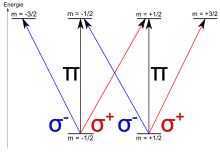
In laser spectroscopy , the circular polarization is divided into ("Sigma-Plus") and ("Sigma-Minus") instead of right and left , which causes a change in the magnetic quantum number of +1 or −1 at atomic transitions between energy levels . Linearly polarized light ( at the atomic transition) is called -polarized light. The advantage of this information is the independence from the coordinate system ( right and left ); instead, the specification refers to the selected quantization axis of the atom.
See also
Individual evidence
- ^ Wilhelm H. Westphal : Physics - A textbook . 25th edition. Springer, 1970, p. 525 .
- ↑ Also in the lecture by Rudolf Gross at the Technical University of Munich, pdf , Technical University of Munich, accessed 2017. There, this convention is described as unfortunate and it is pointed out that in more recent literature the reverse definition is sometimes used (according to the usual convention for helicity ).
- ↑ www.fangschreckenkrebse.de .
- ↑ Stefan Greif, Ivailo Borissov, Yossi Yovel and Richard A. Holland: A functional role of the sky's polarization pattern for orientation in the greater mouse-eared bat. In: Nature Communications. Volume 5, Article No. 4488, 2014, doi: 10.1038 / ncomms5488 .
- ↑ Karl Fent: Polarized skylight orientation in the desert ant Cataglyphis. In: Journal of Comparative Physiology A. Volume 158, No. 2, 1986, pp. 145-150, doi: 10.1007 / BF01338557 .
- ^ Rüdiger Wehner : Polarization vision - a uniform sensory capacity? In: The Journal of Experimental Biology. Volume 204, 2001, pp. 2589-2596, PMID 11511675 .
- ↑ Eduard Von Hartmann: The world view of modern physics. Hermann Haacke Verlagbuchhandlung, Leipzig, 1902 ( limited preview in the Google book search).
- ^ Polarization definitions, Ibsen Photonics
Web links
- Polarization at atomic transitions
- Animation of circular waves with polarizer (requires Java)
- Video from the "one and a half lexicon" about polarization ( slow connection ; fast connection )
- Satellite polarization (PDF; 1.4 MB)
- Video: polarized light . Institute for Scientific Film (IWF) 2004, made available by the Technical Information Library (TIB), doi : 10.3203 / IWF / C-14897 .