The Fresnel formulas (after Augustin Jean Fresnel ) quantitatively describe the reflection and transmission of a flat , electromagnetic wave to a planar interface. The initially calculated reflection and transmission factor is the ratio of the reflected or transmitted amplitude to that of the incident wave. By squaring, the degree of reflection and transmission are obtained, which represent intensity ratios as energy quantities.
Previews
The Fresnel formulas can be derived from Maxwell's equations , using special cases of the boundary conditions of electromagnetic waves at a charge and current-free boundary layer:

|

|

|

|
Here, the normal to the interface and the other quantities describe the magnetic field and electric field in the two media. The tangential component of the electric field strength E and the magnetic field strength H are continuous at the interface, as are the normal components of the electrical flux density D and the magnetic flux density B (tangential and normal refer to the interface).

Depending on the polarization of the incident wave, there are different boundary conditions for the impact of an electromagnetic wave on an optical interface. Every arbitrarily polarized electromagnetic wave can be represented as a superposition of two linearly polarized waves that oscillate perpendicular to each other. The plane of incidence serves as the reference plane, which is spanned by the wave vector of the incident wave and the surface normal . An incident wave polarized as required can be written as a superposition of a wave polarized parallel (p) and perpendicular (s) to the plane of incidence :


![{\ vec {E}} = \ left [(E_ {0e}) _ {s} \ {\ vec {e}} _ {s} \ e ^ {i \ delta _ {s}} + (E_ {0e }) _ {p} \ {\ vec {e}} _ {p} \ e ^ {i \ delta _ {p}} \ right] \ e ^ {i ({\ vec {k}} _ {e} \ cdot {\ vec {r}} - \ omega t)} = (E_ {0e}) _ {s} \ {\ vec {e}} _ {s} \ e ^ {i ({\ vec {k} } _ {e} \ cdot {\ vec {r}} - \ omega t + \ delta _ {s})} + (E_ {0e}) _ {p} \ {\ vec {e}} _ {p} \ e ^ {i ({\ vec {k}} _ {e} \ cdot {\ vec {r}} - \ omega t + \ delta _ {p})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f534963b5e272a51a599d420ff7f0af67de8db19)
Here is the field vector of the electric field, are the unit vectors for s and p polarization, and the parameters correspond to any phase shift.



Because of the superposition principle, it is sufficient to calculate the amplitude ratios for waves linearly polarized parallel and perpendicular to the plane of incidence.
The direction of polarization (perpendicular or parallel to the plane of incidence) remains unchanged after the reflection.
General case
In the general case, the two media have different permittivity and permeability as well as a complex refractive index

-
 .
.
Preview for equations with the angle of refraction eliminated
In general, both the refractive index of the media involved and the angle of incidence and refraction are necessary for calculating the degrees of reflection or transmission using the Fresnel formulas.
In order to specify a form that is independent of the angle of refraction in addition to these general equations, the angle of refraction must be eliminated from the general form. Since both angles ( and ) are linked via Snell's law of refraction , this can be achieved as follows (with the help of a case limitation):


-
 (Law of refraction)
(Law of refraction)
Squaring provides the following relationship (using a trigonometric conversion ):

The changed result:

The case with the positive sign is used as a solution so that the reflection factor r ≤ 1 later .
Vertical polarization
With perpendicular polarization, the electrical component forms a right angle with the plane of incidence.
First, consider the component that is linearly polarized perpendicular (index: s) to the plane of incidence. It is also referred to in the literature as the transverse electrical (TE) component.


With the transmission factor and reflection factor . The coefficients relate to the electric field.


Parallel polarization

With parallel polarization, the electrical component oscillates in the plane of incidence.

Coordinate system for measuring the E-vectors
In the other case, the amplitude of a wave polarized linearly parallel (index: p) in the plane of incidence is considered. It is also referred to in the literature as the transverse magnetic (TM) component. Here the coefficients relate to the magnetic field.


The directions of the electric field vectors or correspond to the directions of the vectors or , where the normal vector is the plane of incidence.





Special case: same magnetic permeability
For the special case that is common in practice that the materials involved have approximately the same magnetic permeability ( ), e.g. E.g. for non-magnetic materials, the Fresnel formulas are simplified as follows:


- Vertical polarization (TE)


- Parallel polarization (TM)


Special case: dielectric materials
Another special case arises for ideal dielectrics in which the absorption coefficient of the complex refractive index is zero. This means that the material on both sides of the interface does not absorb the corresponding electromagnetic radiation ( ). The following applies:


![N_ {i} = n_ {i} (1+ \ mathrm {i} \ kappa _ {i}) = n_ {i} + \ mathrm {i} k_ {i} \ quad {\ xrightarrow [{}] {k_ {i} = 0}} \ quad N_ {i} = n_ {i}](https://wikimedia.org/api/rest_v1/media/math/render/svg/76ea4c5807682bd685b13184b300c7746a7092b5)
By eliminating the complex parts, the Fresnel formulas are simplified as follows:
- Vertical polarization (TE)


- Parallel polarization (TM)


Hint: The second equals sign results from applying the law of refraction and addition theorems . The assumptions made are not valid for angles of incidence of 0 ° and 90 ° and the formulas can therefore not be used. For this, the original form from pure cosine terms must be used

Vertical incidence
A further simplification results for the case that the angle of incidence α is equal to 0 (perpendicular incidence):


For example, if visible light falls perpendicularly onto the air / quartz glass interface , then the proportion will be

the incident intensity is reflected independently of the polarization (see section on the relationship with the degree of reflection and transmittance ).
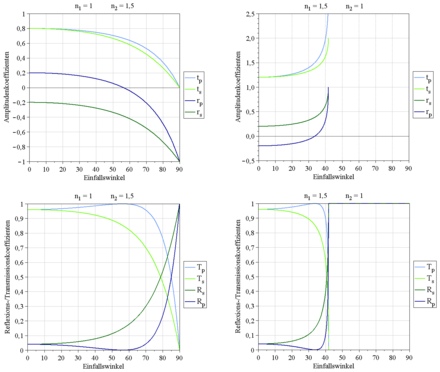
Discussion of the amplitude relationships
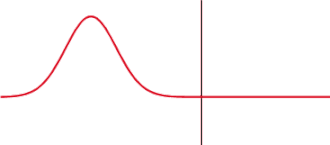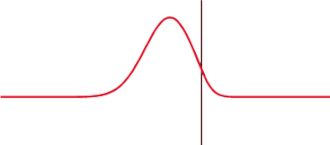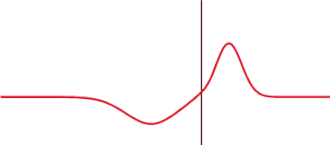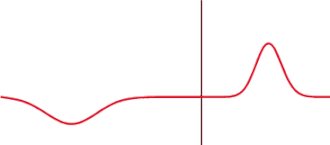
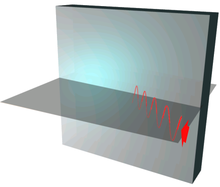
Partial reflection and transmission of a one-dimensional wave at a potential step. The proportion of the reflected and transmitted intensity of an electromagnetic wave can be calculated using Fresnel's formulas.
Where the amplitude coefficients are real and negative, enters phase shift from on (with real and positive no phase change):


The amplitude ratio has a zero crossing at Brewster's angle :


-
 exactly at
exactly at 
-
 so
so 
Examples: Brewster's angle for air-glass is , and for glass-to-air is .




The amplitude relationships become complex from a certain angle. From this critical angle or critical angle , total reflection occurs. The critical angle corresponds to the angle of refraction so , d. i.e., the wave travels along the interface.




-
 so
so 
Example: The critical angle for glass-air is .


Relationship with the degree of reflection and transmission

Influence of the complex refractive index of a material ( ) on the reflection behavior of a light beam when it hits the air / material interface

Consider a bundle of rays that is incident on the interface of an isotropic, non-magnetic material of the surface . The beam cross-sections of the incident, reflected and transmitted beam are , and . The energy that flows per unit of time and area through an area whose normal is parallel to the direction of energy flow (in isotropic media the same direction of propagation ) is given by the complex Poynting vector :








The mean energy flux density is obtained by averaging over time and some transformations:

The average energy that is transported by the beam per unit of time (average power that hits the surface ) corresponds to the average energy flux density times the cross-sectional area, i.e.

-
 , or .
, or .

In general (unpolarized light) the degree of reflection (often also referred to as ρ) is defined as follows:


and as transmittance (often also referred to as τ):


The two values can now be calculated with the help of Fresnel's formulas; they are the product of the corresponding reflection or transmission factor with its conjugate complex value.


For ideal dielectrics that have no absorption and therefore only real-valued refractive indices, the equations simplify to:


with for the s- or p-polarized component.

In addition, the degree of reflection and transmission are linked to one another via the following general energy flow balance at an interface (no absorption, i.e. the degree of absorption is zero):
-
 .
.
literature
-
Wolfgang Nolting : Basic Course Theoretical Physics 3: Electrodynamics. 7th edition. Springer, Berlin 2002, ISBN 3-540-20509-8 .
-
Wolfgang Demtröder : Experimentalphysik 2. Springer, Berlin 2004, ISBN 3-540-20210-2 .
-
John David Jackson : Classical Electrodynamics. de Gruyter, Berlin 2006, ISBN 3-11-018970-4 .
-
Karl J. Ebeling : Integrated optoelectronics: waveguide optics, photonics, semiconductors. 2nd edition, Springer. Berlin 1998, ISBN 3-540-54655-3 .
Web links
Individual evidence
-
↑ a b cf. M. Bass (Ed.): Handbook of Optics. Volume I - Geometrical and Physical Optics, Polarized Light, Components and Instruments . 3. Edition. McGraw-Hill Professional Publishing, 2009, ISBN 978-0-07-162925-6 , pp. 12.6-12.9 .
-
^ Eugene Hecht: Foam's outline of theory and problems of optics . McGraw-Hill Professional, 1975, ISBN 0-07-027730-3 , pp. 40-50 .
-
↑ a b Jay N. damask: Polarization optics in telecommunications . Springer, New York 2005, ISBN 0-387-22493-9 , pp. 10-17 .






![{\ vec {E}} = \ left [(E_ {0e}) _ {s} \ {\ vec {e}} _ {s} \ e ^ {i \ delta _ {s}} + (E_ {0e }) _ {p} \ {\ vec {e}} _ {p} \ e ^ {i \ delta _ {p}} \ right] \ e ^ {i ({\ vec {k}} _ {e} \ cdot {\ vec {r}} - \ omega t)} = (E_ {0e}) _ {s} \ {\ vec {e}} _ {s} \ e ^ {i ({\ vec {k} } _ {e} \ cdot {\ vec {r}} - \ omega t + \ delta _ {s})} + (E_ {0e}) _ {p} \ {\ vec {e}} _ {p} \ e ^ {i ({\ vec {k}} _ {e} \ cdot {\ vec {r}} - \ omega t + \ delta _ {p})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f534963b5e272a51a599d420ff7f0af67de8db19)









































![N_ {i} = n_ {i} (1+ \ mathrm {i} \ kappa _ {i}) = n_ {i} + \ mathrm {i} k_ {i} \ quad {\ xrightarrow [{}] {k_ {i} = 0}} \ quad N_ {i} = n_ {i}](https://wikimedia.org/api/rest_v1/media/math/render/svg/76ea4c5807682bd685b13184b300c7746a7092b5)
















































