vibration
When vibrations or oscillations ( latin oscillare , 'Rock) are repeated time variations of state quantities referred to a system. Fluctuation is to be understood as the deviation from a mean value. Vibrations can occur in all feedback systems. Examples of vibrations can be found in mechanics, electrical engineering, biology, economics and many other areas.
One differentiates:
- periodic and non-periodic (quasi-periodic or chaotic) vibrations
- undamped, damped and aperiodic oscillations
- free, forced (separately excited) , self-excited and parameter-excited vibrations
- linear and non-linear vibrations
- Vibrations with one degree of freedom , with several degrees of freedom and with an infinite number of degrees of freedom (vibrations of a continuum )
- continuous vibrations and oscillation between discrete states
All of these properties can be combined.
Periodic mechanical vibrations of a body associated with deformation are referred to as vibration . An oscillation that is used to convey information is sometimes called a signal, for example an electrical signal . The spatial propagation of a disturbance or vibration is a wave .
Harmonic oscillations
 |
| Representation of a harmonic oscillation. |
An oscillation is called harmonic , the course of which can be described by a sine function .
The graphic shows a harmonic oscillation with the deflection , the amplitude and the period .
The deflection at a point in time indicates the current value, the amplitude the maximum possible value of the variable . The period or the period of oscillation is the time that elapses while an oscillatable system runs through exactly one oscillation period, i.e. H. after which it is again in the same vibrational state. The reciprocal of the period T is the frequency f , ie: . The Greek letter (read: "nü") is used instead of f . The unit of frequency is Hertz (1 Hz = 1 s −1 ).
An undamped oscillation is harmonic if the restoring variable (the restoring force ) is proportional to the deflection of a spring pendulum , for example . This is also called a harmonic oscillator or a linear system , since the restoring force changes linearly with the deflection: If this doubles, the restoring force also doubles.
Such a vibration can be described by
With
- = Amplitude and
- = Zero phase angle of the oscillation.
The -fold of the frequency, is the angular frequency of the oscillation. Using the angular frequency results in a more compact notation:
Linear damped oscillation
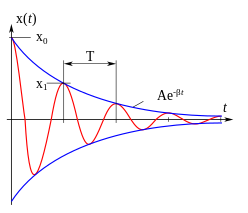 
|
| Representation of the time course of the variable with a free damped oscillation.
|
Macroscopic physical systems are always dampened . Since they give off energy to the environment through friction, for example , the amplitude of their oscillation decreases over time. If such a system is left to its own devices (free oscillation), this ultimately leads to a “standstill”, as can be seen from the second law of thermodynamics . Perpetua mobilia are therefore not possible (see the law of conservation of energy ).
If you set up the equation of motion of a spring pendulum with a damping proportional to the speed, the following differential equation results:
It is
- the crowd ,
- the damping constant and
- the spring constant .
(For torsional vibrations , replace with the moment of inertia and the deflection angle .)
This is a homogeneous linear ordinary differential equation of the 2nd order, referring to the general form
if you can use the (positive) abbreviations for the decay constant
and the undamped natural angular frequency
introduces whose meanings only become clear when the solution is interpreted.
In the classical way of solving such a linear homogeneous differential equation (alternatively one can use methods of operator calculus ), with the help of the approach
With possibly complex parameters, two linearly independent solutions can be found which form a fundamental system. Inserted into the differential equation results in:
- .
In this equation, only the expression in brackets can be zero. The so-called characteristic equation for determining the constant is obtained :
That is a quadratic equation , its discriminant
determines whether it has two real solutions, two complex conjugate solutions or a so-called double root. A distinction between cases is therefore necessary.
The theory of linear differential equations shows that the general solution of the homogeneous differential equation is a linear combination of the two solutions found. If the characteristic equation has two solutions (i.e. the discriminant is not equal to 0), then the general solution of the equation of motion can be written as follows:
The two (generally complex) constants and represent the two remaining degrees of freedom of the general solution. By defining two initial conditions (e.g. and / and ), the two constants must be specified for a specific case.
Vibration case
There can only be an oscillation if the losses are low. Then the discriminant is negative, the root expression is imaginary and we get two complex conjugate solutions:
- .
With the damped natural angular frequency:
- .
results in shorter:
- .
So you get
With the help of Euler's formulas , the solution of the homogeneous differential equation can also be given in trigonometric form. In the theory of linear differential equations with constant coefficients it is shown that this (in contrast to the exponential form) is purely real and therefore easier to interpret in practice:
or
Here, too, the two constants and or and are to be determined by the initial conditions. The last form in particular can easily be interpreted as a “damped oscillation”.
By specifying the two initial conditions and , the two constants can be eliminated. Based on the first trigonometric form, the concrete solution that depends on both initial conditions is obtained
When the decay constant is zero, the amplitude remains constant. The oscillation is undamped with the angular frequency .
Aperiodic borderline case
The limit from which oscillation is no longer possible is the aperiodic limit case ( or ). The solution then does not contain a sine function. Since the following applies, a second solution that is too independent must be constructed in a different way. It turns out
Creep fall
With high damping, i.e. for , the creep case results , the solution of which is made up of two exponential functions with the two real ones:
- .
Frequency spectrum of an oscillation
An oscillation can also be viewed as a function in the frequency domain instead of a time-dependent change . The mathematical transformation is called Fourier transformation. The information content is retained, which is why the corresponding time-dependent oscillation can always be reconstructed from a frequency spectrum by reverse transformation. The background to this consideration is that every oscillation can be represented by an additive superposition ( superposition ) of harmonic oscillations of different frequencies. The superposition of two harmonic oscillations is called beat .
Excitation of an oscillation
Free vibrations
Free oscillations are carried out by a system capable of oscillation, which - left to its own devices after a disturbance / deflection - returns to the state of equilibrium in an oscillating or "creeping" manner depending on the damping (see above). The frequency of the free oscillation is the natural frequency of the oscillator. In the case of vibrations with several degrees of freedom, there are correspondingly many natural frequencies.
Forced vibrations
Forced vibrations are carried out by a vibrator that is excited (forced) to vibrate by external influences that vary over time. Periodic excitations, including harmonic, sinusoidal excitation, are of particular practical importance. The frequency of the periodic excitation is called the excitation frequency. There are also multi-frequency excitations or excitations by chance processes.
In the case of harmonic excitation, a linear system generally performs two oscillations at the same time:
- the free oscillation (with the natural frequency or several natural frequencies), the size of which depends on the initial conditions and which decays due to the damping that is always present during the settling time and
- the forced oscillation with the excitation frequency at constant excitation strength. The amplitude of this oscillation is constant after the transient process has ended. The relationship between the amplitude and the strength of the excitation is quantified by the magnification function.
In technical mechanics , the most important excitation mechanisms are path excitation , force excitation and imbalance excitation (see magnification function ).
The amplitude of the forced oscillation assumes a maximum in the case of resonance . If there is no damping and equality of (one) excitation frequency and (one) natural frequency, the amplitude becomes infinite. As the damping value increases, the resonance point shifts slightly and the resonance amplitude decreases.
Self-excited vibrations
Vibration systems in which the energy supply is controlled by a suitable control element and the vibration process itself, carry out self-excited vibrations and are called oscillators . In the differential equations, this phenomenon has the effect that the damping value becomes zero. A typical example in the field of mechanics is the vibrations of the strings of a violin. These are caused by the fact that the static friction between bow and string is greater than the sliding friction and the sliding friction still decreases with increasing differential speed. Further examples are the tinting of glasses by rubbing the edge and electronic clock generators ( oscillator circuit ).
Self-excited oscillations increase in amplitude until the damping, which increases disproportionately with the amplitude, compensates for the energy coupling or the oscillating system is destroyed.
Parameter-excited vibrations
A parameter-excited oscillation occurs when parameters of the oscillation system (inertia quantities, damping values or spring constants) change periodically, e.g. B. when rocking .
Linear and non-linear vibrations
Linear oscillations are characterized by the fact that they can be described with differential equations in which all dependencies on the oscillating quantity and its time derivatives are linear . This is not the case with non-linear vibrations, so they are not strictly sinusoidal. It is of greater practical importance that the resonance behavior of forced vibrations changes with a driven oscillator and the amplitudes of self-excited vibrations remain limited.
Nonlinear systems are often not integrable ; H. the differential equation (s) have no analytical solution . The vibration behavior of such systems is therefore mostly investigated with numerical computer simulations . One of the first of these experiments was the Fermi-Pasta-Ulam experiment , in which a string vibration with a non-linear disturbance term was investigated. As a solution to such systems, depending on the energy of the oscillation, a quasi-periodic or chaotic oscillation is often obtained . Chaotic behavior can be observed , for example, with a double pendulum . A non-linear system that does not allow chaotic behavior is the van der Pol oscillator .
Vibrations with several degrees of freedom

Vibrations with one degree of freedom are those that can be fully described with one vibrating quantity. An example of this are vibrations of the flat thread pendulum . If the pendulum is allowed to move in space like a Foucault pendulum , it is already an oscillator with two degrees of freedom. In the following, we limit ourselves to the consideration of small deflections.
This example shows that the designation as an oscillation can depend on the quantities considered, i.e. the choice of generalized coordinates . This allows the pendulum to be deflected so that the oscillation takes place in one plane. If you also give the pendulum an initial speed perpendicular to the direction of deflection, you can observe elliptical orbits or a circular movement with constant angular speed .
If you look at the deflection angle of the pendulum from two different directions, you get two harmonic oscillations with the same period. A superposition of two harmonic oscillations is called a Lissajous figure . Another possibility is to look at the pendulum from above and note the distance to the rest position as well as the direction of the deflection as a continuous distance to the starting angle. In the case of a circular path, both are no longer vibrations.
The number of degrees of freedom of a mechanical system with several masses that can move independently of one another is the sum of all individual degrees of freedom. Further examples of vibrations with several degrees of freedom are torsional vibrations of a crankshaft or the horizontal vibrations of a multi-storey building under the influence of earthquakes.
Some vibrations of a system with several degrees of freedom can be considered as several independent vibrations with a suitable choice of coordinates. For a vibration that can be described using differential equations, this means decoupling the equations of the individual coordinates. If the individual vibrations are periodic, the natural frequencies of the system can then be determined from the decoupled differential equations. If all natural frequencies can be written as integer multiples of a constant, then the oscillation of the entire system is also periodic.
In the case of non-linear oscillation systems, decoupling of the differential equations in a closed form is usually not possible. However, approximation methods exist which, based on a linearization of the differential equations, enable an iterative solution.
Vibrations of a continuum

An oscillation excited at one point in a continuum propagates as a wave . The wave can be reflected at interfaces where the propagation medium changes. Within the vibrating body, the original and reflected waves overlap, so that a standing wave is created; Examples are a vibrating string of a musical instrument - geometrically one-dimensional - or the two-dimensional vibrating membrane in a loudspeaker . The standing wave can be mathematically described by an infinite number of coupled oscillators , i.e. a system with an infinite number of degrees of freedom.
The vibrations of rods , plates and bowls are also of practical interest in engineering . A beam clamped on one side has many degrees of freedom of oscillation, which differ not only in their resonance frequencies , but also in the nature of their movement.
Waveform of a beam clamped on one side at the lowest natural frequency - first transverse bending mode
Vibration form of the same beam at a higher natural frequency - second vertical bending mode
Vibration form of the same beam at a higher natural frequency - first torsion mode
Vibration form of the same beam at a higher natural frequency - second torsion mode
Further examples
In everyday life we encounter vibrations, for example, in musical instruments and on clock pendulums, but also in quartz crystals in clocks or for clock generation in other electronic devices.
The atoms in a crystal lattice or molecules can also oscillate around an equilibrium position and thus produce, for example, characteristic absorption spectra .
Oscillating reactions set the pace for breathing and heartbeat.
In electron tubes often microphonic observed. It is caused by disruptive mechanical vibrations acting on the components from the outside, for example from loudspeakers standing nearby.
In manufacturing technology, the regenerative effect is the term used to describe vibrations that occur within a machine during the manufacturing process.
In geology and meteorology, smaller and with a certain regularity recurring fluctuations in the sea level , the ice edge layers , the pieces of the earth's crust, the earth's magnetic field or the climate are observed.
In the economy, the Goodwin model is used to explain business cycles.
The Lotka-Volterra equations approximately describe the fluctuations of predator and prey populations.
See also
- Harmonograph
- Human vibrations , mechanical vibrations that affect people
- Vibrations , oscillations of materials and bodies
- Pointer model
literature
- Hans Dresig , Alexander Fidlin : Vibrations and mechanical drive systems: modeling, calculation, analysis, synthesis . 3rd, revised. and exp. Edition. Springer Vieweg Verlag, Berlin / Heidelberg 2014, ISBN 978-3-642-24116-1 .
- NN Bogoliubow, YA Mitropolski: Asymptotic Methods in the Theory of Non-Linear Oscillations . 2nd Edition. Hindustan pub. Corp. / Gordon and Breach Science Publishers, Delhi / New York / London 1961, OCLC 564000480 (English, table of contents - limited preview).
- Th. Frey, M. Bossert : Signal and System Theory . In: Teubner Informationstechnik . Teubner Verlag, Stuttgart / Leipzig / Wiesbaden 2004, ISBN 3-519-06193-7 .
- Anatole Katok , Boris Hasselblatt : Introduction to the modern theory of dynamical systems . In: Encyclopedia of mathematics and its applications . tape 54 . Cambridge University Press, Cambridge 1996, ISBN 0-521-57557-5 (English).
Web links
Individual evidence
- ↑ Kurt Magnus, Karl Popp: Vibrations . 7th edition. Teubner, 2005, ISBN 3-519-52301-9 , pp. 13 ( limited preview in the Google book search): "Vibrations are more or less regularly occurring temporal fluctuations of state variables."
- ↑ DIN 1311-1: 2000: Vibrations and systems capable of vibrating - Part 1: Basic terms, classification. Section 3 “An oscillation is a change in a state variable of a system over time, in which this state variable generally increases and decreases alternately. Special changes over time such as shock and creep processes are also referred to as vibrations in a broader sense. "
- ↑ 13 vibrations. (PDF; 92 kB) TU Cottbus.
- ↑ Rudolf Jürgler: Machine dynamics . 3rd, revised edition. Springer, 2004, ISBN 3-540-62227-6 , pp. 3 ( limited preview in Google Book Search).
- ↑ Michel Hénon: Numerical exploration of Hamiltonian Systems. Iooss, Helleman, Stora (Eds.): Chaotic Behavior of Deterministic Systems. North-Holland, 1983, pp. 53-76.
- ^ Steven H. Strogatz: Nonlinear Dynamics and Chaos . Perseus Books, 2001, pp. 273 ff., Chapter 8.6 - Coupled Oscillators and Quasiperiodicity .
- ↑ Vladimir Ivanovich Smirnov : Course of higher mathematics . 8th edition. tape 2 . German Publishing House of Science, Berlin 1968, DNB 368242544 .




























































