State variable
A state variable is a macroscopic physical variable that - possibly together with other state variables - describes the state of a physical system , but is viewed as a variable in the context of the observation. If all the state variables of a system remain constant over time, the system is in thermodynamic equilibrium or in a steady flow equilibrium . The state variables describe the current state of a system and are independent of the way in which this state came about. Opposed to them are process variables such as work and heat , which describe the course of a change in state.
In thermodynamics one looks at
- intensive state variables such as pressure and ( absolute ) temperature
-
extensive state variables such as volume , number of particles or amount of substance and entropy
- the thermodynamic potentials : internal energy , free energy , enthalpy , Gibbs energy and the grand-canonical potential , which are also extensive state variables.
Further state variables are derived from this.
Some relationships between the state variables are described by the Maxwell relations and the Guggenheim square .
Classification
There are two basic subdivisions within the state variables: on the one hand into external and internal and on the other hand into intensive and extensive state variables. The thermodynamic potentials stand out among the latter.
Extensive state variables are state variables whose measure scales with the size of the system. Intensive state variables are state variables, the extent of which does not depend on the size of the system. If, for example, one divides a system into two parts that are equal in every respect, every extensive state variable assumes half the value; if one unites two systems with the same type of state variable, it assumes twice the value. Intensive state variables do not change their value as a result.
Example: The amount of liquid in a glass is an extensive quantity, since two glasses contain twice the amount of liquid. The temperature of the liquid, on the other hand, is an intense variable, since two glasses are not twice as warm as a single one.
Extensive state variables
State functions or thermodynamic potentials

The thermodynamic potentials internal energy , free energy , enthalpy and Gibbs energy as well as the grand-canonical potential are extensive state variables. With their information content, they describe the thermodynamic system completely.
The thermodynamic potentials are measured against an arbitrarily set zero point - such as B. the initial state. Then the change in internal energy with the natural variables entropy and volume corresponds to the heat and work supplied :
or expressed as a complete differential:
- .
They differ in their natural variables, which in turn are state variables and can be converted into one another with the help of the Legendre transformation . This results in z. B. the enthalpy with its natural variables entropy and pressure as:
and its full differential is:
- .
Extensive state variables
When considering the thermodynamic potentials, the following extensive state variables are included as natural variables: volume , entropy and number of particles or amount of substance . In dynamic systems or systems influenced by energy-storing fields, the … currents or … flows are also extensive state variables.
Intensive state variables
When considering the thermodynamic potentials, the following intensive state variables are included as natural variables: pressure , (absolute) temperature and chemical potential . The change in an intense quantity always results in a change in the thermodynamic equilibrium. In dynamic systems or systems influenced by energy-storing fields, the speeds and field strengths are also intensive state variables.
Combinations
Combinations of intensive state variables of the same state are in turn intensive state variables. Those of an extensive and an intensive magnitude are extensive. Such combinations appear as the difference in thermodynamic potentials. In this context, one size is always multiplied by its conjugate size. An example of this is the move work . It represents the difference between the enthalpy and the internal energy. It bears the name of a … work , but unlike others … work is not a process variable.
Connections
Equations of state
Experimental results show that the named variables cannot be changed independently of one another, which is also expressed in Gibbs' phase rule or in the definition of the state of a system to a certain number of degrees of freedom . The corresponding relationships between the state variables of a system describe equations of state .
Gases under normal conditions can be roughly described by ideal gas . The general gas equation applies
with the general gas constant .
The Van der Waals equation provides a better approximation for real gases :
- .
Maxwell Relationships
The Maxwell relations or Maxwell relations of thermodynamics (after the physicist James Clerk Maxwell ) describe the relationships between changes in the various state variables. B. the change in temperature or entropy with the help of changes in other state variables, z. B. pressure or volume , express:
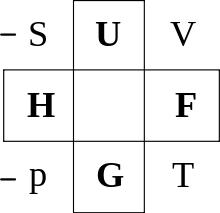
Guggenheim Square
The Guggenheim Square, or Guggenheim Scheme, is a tool for establishing some simple but fundamental relationships in thermodynamics from memory. They can be applied both to the Maxwell relationships and to the characteristic functions . The entropy S, the internal energy U, the volume V, the free energy F (also Helmholtz energy A), the temperature T, the Gibbs energy G, the pressure p, and the enthalpy H are linked .
It is named after Edward Guggenheim .
Memory aids for three degrees of freedom
The Guggenheim square describes systems with two degrees of freedom. Memory aids in the form of the geometric figures octahedron and cuboctahedron have been described for three degrees of freedom. In contrast to the square, the thermodynamic potentials (G, U, H, A etc.) are not edges, but surfaces.
literature
- Literature on technical thermodynamics
- Jibamitra Ganguly: Thermodynamics in earth and planetary sciences . 2008, Thermodynamic Square: A Mnemonic Tool, p. 59-60 ( Google Books [accessed September 15, 2011]).
- Wedler, Gerd: Textbook of physical chemistry . 2nd Edition. VCH, 1985, ISBN 978-3-527-29481-7 , 2.3.2 - Characteristic thermodynamic functions, p. 252-256 .
Web links
- The Guggenheim scheme. Archived from the original on July 24, 2007 ; accessed on September 15, 2011 .
Individual evidence
- ^ LT Klauder. In: American Journal of Physics , 1968 , 36 (6), pp. 556-557, doi: 10.1119 / 1.1974977
- ↑ James M. Phillips. In: J. Chem. Educ. , 1987 , 64 (8), pp. 674-675, doi: 10.1021 / ed064p674
- ↑ Ronald. F. Fox. In: J. Chem. Educ. , 1976 , 53 (7), pp. 441-442, doi: 10.1021 / ed053p441