Thermodynamic potential

Thermodynamic potential are thermodynamics sizes of their information content fro the behavior of a thermodynamic system in equilibrium fully described. The independent state variables of a thermodynamic potential are called its natural variables if their derivative of the potential is equal to one of the dependent state variables (for example:) . A thermodynamic potential corresponds to the information content of the internal energy , the natural variables of which are all extensive ( fundamental equation ). ${\displaystyle \left(\partial U/\partial S\right)_{V,N}=T}$ ${\displaystyle U}$ ${\displaystyle S,V,N}$

Thermodynamic potentials, which are energies, can be derived from the internal energy by Legendre transformation , but, unlike this, have one or more intense quantities as natural variables . The intensive quantities arise during the coordinate transformation as derivatives of the internal energy according to its extensive variables. ${\displaystyle U(S,V,N)}$ ${\displaystyle (T,p,\mu )}$

There are also other thermodynamic potentials that are not energies, for example entropy . ${\displaystyle S(U,V,N)}$

The term thermodynamic potential was generalized by Gottfried Falk to the term Massieu-Gibbs functions (according to Josiah Willard Gibbs ), which are corresponding state functions in not necessarily thermodynamic systems.

Physical meaning

An extreme value (not always a minimum) of a thermodynamic potential indicates the thermodynamic equilibrium .

After connecting one closed system to another, a thermodynamic equilibrium has been established as soon as the entropy of the entire system is at its maximum. In this case, all intensive parameters of the two systems are also the same:

${\displaystyle {\begin{aligned}T_{1}&=T_{2}\\p_{1}&=p_{2}\\\mu _{1}&=\mu _{2}\end{aligned}}}$

In addition, thermodynamic potentials summarize the equations of state of the system, since these are accessible by differentiating a thermodynamic potential according to its dependent variables.

description

The internal energy and the functions resulting from it by means of the Legendre transformation are thermodynamic potentials (with one exception , see below). The Legendre transformation transforms the potentials ${\displaystyle U(S,V,N)}$ ${\displaystyle K}$

• from entropy to temperature , there ${\displaystyle S}$ ${\displaystyle T}$ ${\displaystyle {\frac {\partial U}{\partial S}}=T}$
• from volume to pressure , there ${\displaystyle V}$ ${\displaystyle p}$ ${\displaystyle {\frac {\partial U}{\partial V}}=-p}$
• from particle number to chemical potential , there ${\displaystyle N}$ ${\displaystyle \mu }$ ${\displaystyle {\frac {\partial U}{\partial N}}\,=\mu }$

Because of these 3 pairs of variables there are possible thermodynamic potentials: ${\displaystyle 2^{3}=8}$

Thermodynamic Potentials

Name (alternative name)	Formula symbol	natural variables (intense bold)	Characteristic function f	Connections
Inner energy	${\displaystyle U}$	${\displaystyle S,V,N}$	${\displaystyle \mathrm {d} U=TdS-pdV+\mu {d}N}$	${\displaystyle U(S,V,N)=TS-pV+{\sum _{i=1}^{K}}\,\mu _{i}N_{i}.}$ ( Euler equation for the internal energy )
Free energy (Helmholtz potential)	${\displaystyle F}$	${\displaystyle {\boldsymbol {T}},V,N}$	${\displaystyle \mathrm {d} F=-SdT-pdV+\mu {d}N}$	${\displaystyle F=U(S,V,N)-TS}$
Enthalpy	${\displaystyle H}$	${\displaystyle S,{\boldsymbol {p}},N}$	${\displaystyle \mathrm {d} H=TdS+Vdp+\mu {d}N}$	${\displaystyle H=U(S,V,N)\qquad \ +pV}$
Gibbs energy (free enthalpy)	${\displaystyle G}$	${\displaystyle {\boldsymbol {T}},{\boldsymbol {p}},N}$	${\displaystyle \mathrm {d} G=-SdT+Vdp+\mu {d}N}$	${\displaystyle {\begin{aligned}G&=U(S,V,N)-TS+pV\\&=H(S,p,N)-TS\\&=F(T,V,N)\qquad \quad +pV\end{aligned}}}$
-	${\displaystyle R}$	${\displaystyle S,V,{\boldsymbol {\mu }}}$	${\displaystyle \mathrm {d} R=TdS-pdV-N{d}\mu }$	${\displaystyle R=U(S,V,N)\qquad \qquad \quad -\mu N}$
Grand canonical potential	${\displaystyle \Omega }$	${\displaystyle {\boldsymbol {T}},V,{\boldsymbol {\mu }}}$	${\displaystyle \mathrm {d} \Omega =-S{d}T-p{d}V-N{d}\mu }$	${\displaystyle {\begin{aligned}\Omega &=U(S,V,N)-TS\qquad \ -\mu N\\&=R(S,V,\mu )-TS\\&=F(T,V,N)\qquad \qquad \quad -\mu N\end{aligned}}}$
-	${\displaystyle J}$	${\displaystyle S,{\boldsymbol {p}},{\boldsymbol {\mu }}}$	${\displaystyle \mathrm {d} J=TdS+Vdp-N{d}\mu }$	${\displaystyle {\begin{aligned}J&=U(S,V,N)\qquad \quad +pV-\mu N\\&=R(S,V,\mu )\qquad \quad +pV\\&=H(S,p,N)\qquad \quad \qquad -\mu N\end{aligned}}}$
-	${\displaystyle (K)}$	${\displaystyle {\boldsymbol {T}},{\boldsymbol {p}},{\boldsymbol {\mu }}}$ Not useful because the Gibbs-Duhem relation forbids the independent specification of the variables . ${\displaystyle T,p,\mu }$	${\displaystyle \mathrm {d} K=-SdT+Vdp-N{d}\mu }$	${\displaystyle {\begin{aligned}K&=U(S,V,N)-TS+pV-\mu N=0\\&=J(S,p,\mu )-TS\\&=\Omega (T,V,\mu )\qquad \quad +pV\\&=G(T,p,N)\qquad \quad \qquad -\mu N\end{aligned}}}$

Guggenheim Square

All meaningful thermodynamic potentials, which result from U (S, V, N) by Legendre transformation, provide the same, complete information about a system. The simplest description of the system, however, only provides one of the potentials depending on the ensemble ; this is extremal in equilibrium.

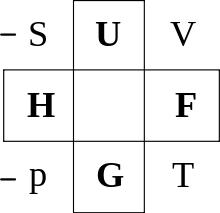
One way of memorizing thermodynamic potentials with their natural variables is the Guggenheim square .

Example of transformation

As an example, the change from one potential to the other is to be carried out using characteristic functions ( total differentials ).

The aim is to transform from the internal energy  U with the natural variables to a new potential with the natural variables . We start with the inner energy: ${\displaystyle S,V,N}$ ${\displaystyle T,V,N}$

${\displaystyle {\begin{aligned}\mathrm {d} U(S,V,N)&={\frac {\partial U}{\partial S}}\,\mathrm {d} S+{\frac {\partial U}{\partial V}}\,\mathrm {d} V+{\frac {\partial U}{\partial N}}\,\mathrm {d} N\\&=T\,\mathrm {d} S-p\,\mathrm {d} V+\mu \,\mathrm {d} N\end{aligned}}}$

With

${\displaystyle {\begin{aligned}\mathrm {d} (TS)&=T\,\mathrm {d} S+S\,\mathrm {d} T\\\Leftrightarrow T\,\mathrm {d} S&=\mathrm {d} (TS)-S\,\mathrm {d} T\end{aligned}}}$

follows

${\displaystyle \Rightarrow \mathrm {d} U=\mathrm {d} (TS)-S\,\mathrm {d} T-p\,\mathrm {d} V+\mu \,\mathrm {d} N.}$

Now bring to the left: ${\displaystyle \mathrm {d} (TS)}$

${\displaystyle {\begin{aligned}\Leftrightarrow \mathrm {d} (U-TS)&=-S\,\mathrm {d} T-p\,\mathrm {d} V+\mu \,\mathrm {d} N=:\mathrm {d} F\\&={\frac {\partial F}{\partial T}}\,\mathrm {d} T+{\frac {\partial F}{\partial V}}\,\mathrm {d} V+{\frac {\partial F}{\partial N}}\,\mathrm {d} N\end{aligned}}}$

The new potential now depends on the natural variables and is called "free energy  ". It is the Legendre transform of U (S, V, N) with respect to the variable S. ${\displaystyle U-TS}$ ${\displaystyle T,V,N}$ ${\displaystyle F}$

Equations of state

Let be any thermodynamic potential, then its total differential can be written as ${\displaystyle \Phi }$

${\displaystyle \mathrm {d} \Phi =\sum _{i}x_{i}\cdot \mathrm {d} y_{i}}$

in which

• ${\displaystyle y_{i}}$the natural variables of are and ${\displaystyle \Phi }$
• ${\displaystyle x_{i}}$ the respective conjugated variables.

From the chain rule follows:

${\displaystyle x_{j}={\frac {\partial \Phi }{\partial y_{j}}}{\Bigg |}_{\{y_{i\neq j}\}}}$

Here is the set of all natural variables of none . They are expressions of thermodynamic parameters as a function of derivatives of the thermodynamic potential, which depends on its natural variables. The so is precisely the state functions of the system. ${\displaystyle \{y_{i\neq j}\}}$ ${\displaystyle \Phi }$ ${\displaystyle y_{i}}$ ${\displaystyle x_{j}}$ ${\displaystyle x_{j}}$

Individual evidence

1. ↑ ^{a b c} Wolfgang Nolting : Basic course in theoretical physics. Volume 6: Statistical Physics. 6th edition. Springer, Berlin et al. 2007, ISBN 978-3-540-68870-9 , p. 373 ff., ( Google Books ).
2. ↑ Wolfgang Nolting: Basic course in theoretical physics. Volume 4: Special Theory of Relativity, Thermodynamics. 6th, updated edition. Springer, Berlin et al. 2005, ISBN 3-540-24119-1 , p. 206.
3. ↑ Gottfried Falk : Theoretical Physics. On the basis of a general dynamic (= Heidelberg pocket books. ). 2 volumes (Vol. 1: Elementary Point Mechanics . Vol. 2: General Dynamics, Thermodynamics. 7 and 27, ISSN  0073-1684 ). Springer, Berlin et al. 1966–1968.
4. ↑ Gottfried Falk, Wolfgang Ruppel : Energy and Entropy. An introduction to thermodynamics. Springer, Berlin et al. 1976, ISBN 3-540-07814-2 .
5. ↑ Christoph Strunk: Modern Thermodynamics. 2015, pp. 144 ff., ( Google Books ).
6. ↑ Walter Greiner , Ludwig Neise, Horst Stöcker : Thermodynamics and statistical mechanics (= Theoretical Physics. Vol. 9). 2nd, completely revised and enlarged edition. Deutsch, Thun et al. 1993, ISBN 3-8171-1262-9 , p. 150.
7. ^ Callen: Thermodynamics and an Introduction to Thermostatistics. 2nd edition. 1985, p. 37.

literature

• Herbert B. Callen : Thermodynamics and an Introduction to Thermostatistics. 2nd edition. Wiley & Sons, New York NY et al. 1985, ISBN 0-471-86256-8 .
• Ulrich Nickel: Textbook of Thermodynamics. A clear introduction. 3rd, revised edition. PhysChem, Erlangen 2019, ISBN 978-3-937744-07-0 .
• Christoph Strunk: Modern Thermodynamics. From simple systems to nanostructures. de Gruyter, Berlin et al. 2015, ISBN 978-3-11-037105-5 , ( Google Books ).