Differential calculus
The differential or differential calculus is an essential part of analysis and thus a field of mathematics . It is closely related to integral calculus , with which it is collectively referred to as infinitesimal calculus . The central topic of differential calculus is the calculation of local changes in functions . The derivation of a function (also called differential quotient ), the geometric equivalent of which is the tangent slope, is useful for this and at the same time the basic concept of differential calculus . The derivative is (according to Leibniz's idea ) the proportionality factor between vanishingly small (infinitesimal) changes in the input value and the resulting, likewise infinitesimal changes in the function value. If such a proportionality factor exists, the function is called differentiable. Equivalently , the derivative at a point is defined as the slope of that linear function that locally best approximates the change in the function at the point under consideration of all linear functions . Accordingly, the derivative is also called the linearization of the function.
In many cases, differential calculus is an indispensable tool for creating mathematical models that are supposed to represent reality as precisely as possible, as well as for their subsequent analysis. The equivalent of the derivative in the examined facts is often the current rate of change . For example, the derivation of the position or distance-time function of a particle in terms of time is its instantaneous speed and the derivation of the instantaneous speed in terms of time provides the instantaneous acceleration. In economics, one often speaks of marginal rates instead of derivation (e.g. marginal costs , marginal productivity of a production factor, etc.).
This article also explains the mathematical terms: difference quotient, differential quotient, differentiation, continuously differentiable, smooth, partial derivative, total derivative, reduction of the degree of a polynomial.
In geometric language, the derivative is a generalized slope. The geometric term slope was originally only defined for linear functions whose function graph is a straight line. The derivative of any function at a point is defined as the slope of the tangent at the point on the graph of .
In arithmetic language, the derivative of a function indicates for each how large the linear portion of the change in is (the 1st order change) if changes by an arbitrarily small amount . The term limit value (or Limes ) is used for the exact formulation of this fact .
history
The task of differential calculus developed as a tangent problem from the 17th century. An obvious solution was to approximate the tangent to a curve through its secant over a finite ( finite here means: greater than zero) but arbitrarily small interval . In doing so, the technical difficulty had to be overcome to calculate with such an infinitesimally small interval width. The first beginnings of differential calculus go back to Pierre de Fermat . Around 1628 he developed a method to determine extreme points of algebraic terms and to calculate tangents to conic sections and other curves. His "method" was purely algebraic. Fermat did not look at any border crossings and certainly not at any derivations. Nonetheless, his “method” can be interpreted and justified with modern means of analysis, and it has demonstrably inspired mathematicians like Newton and Leibniz. A few years later, René Descartes chose a different algebraic approach by adding a circle to a curve. This intersects the curve at two points that are close together; unless it hits the curve. This approach enabled him to determine the gradient of the tangent for special curves.
At the end of the 17th century, Isaac Newton and Gottfried Wilhelm Leibniz succeeded independently of one another in developing calculi that worked without contradictions (for the history of discovery and the dispute over priority, see the history of calculus ). Newton approached the problem from a different angle than Leibniz. While Newton tackled it physically via the instantaneous velocity problem, Leibniz solved it geometrically via the tangent problem. Her work allowed the abstraction of purely geometric ideas and is therefore seen as the beginning of analysis. They were best known through the book by the nobleman Guillaume François Antoine, Marquis de L'Hospital , who took private lessons from Johann I Bernoulli and published his research on analysis. The derivation rules known today are mainly based on the works of Leonhard Euler , who coined the term function. Newton and Leibniz worked with arbitrarily small positive numbers. This was already criticized as illogical by contemporaries, for example by George Berkeley in the polemical work The analyst; or, a discourse addressed to an infidel mathematician. It was not until the 1960s that Abraham Robinson was able to put this use of infinitesimal quantities on a mathematically and axiomatically secure foundation (see: Nonstandardanalysis ). Despite the prevailing uncertainty, differential calculus was consistently developed, primarily because of its numerous applications in physics and other areas of mathematics. The competition published by the Prussian Academy of Sciences in 1784 was symptomatic of the time :
“… The higher geometry often uses infinitely large and infinitely small sizes; however, the ancient scholars carefully avoided the infinite, and some famous analysts of our day admit that the words infinite greatness are contradictory. The academy therefore demands that you explain how so many correct sentences arose from a contradicting assumption, and that you give a safe and clear basic term which could replace the infinite without making the calculation too difficult or too long ... "
It was not until the beginning of the 19th century that Augustin-Louis Cauchy succeeded in giving differential calculus the logical rigor that is customary today by deviating from the infinitesimal quantities and defining the derivative as the limit value of secant gradients ( difference quotients ). The definition of the limit value used today was finally formulated by Karl Weierstrass at the end of the 19th century.
definition
introduction
The starting point for the definition of the derivative is the approximation of the tangent slope by a secant slope (sometimes also called chord slope). Find the slope of a function at a point . First one calculates the slope of the secant an over a finite interval :
- Secant slope = .
The secant slope is therefore the quotient of two differences; it is therefore also called the difference quotient . With the short notation for one can write the secant slope abbreviated as .
Difference quotients are well known from everyday life, for example as average speed:
“On the drive from Augsburg to Flensburg, I was at the Biebelried junction at 9:43 am (daily mileage ). At 11:04 a.m. ( ) I was at the triangle Hattenbach (daily mileage ). In 1 hour and 21 minutes ( ) I covered 143 km ( ). My average speed on this section was ( ). "
In order to calculate a tangent gradient (i.e. an instantaneous speed in the application example mentioned), the two points through which the secant is drawn must be moved closer and closer to one another. Here, both go as well to zero. In many cases, however, the quotient remains finite. The following definition is based on this border crossing :
Differentiability
A function that maps an open interval into the real numbers is called differentiable at the point if the limit value
- (with )
exists. This limit value is called the differential quotient or derivative from to at the point and is called
- or or or
written down. These notations are spoken as “f dash from x zero”, “df from x to dx at the point x equals x zero”, “df to dx from x zero” or “d to dx from f from x zero”. In the later section Notations , further variants are given for noting the derivative of a function.
Over time, the following equivalent definition has been found, which has proven to be more powerful in the more general context of complex or multi-dimensional functions:
A function is said to be differentiable at a point if a constant exists such that
The increase in function , when speaking of himself only slightly away, about the value , can be so by approximate Good is called the linear function with that is why the linearization of at the site .
Another definition is: There is a place on the continuous function with and a constant such that for all true
- .
The conditions and that is continuous at the point just mean that the “remainder term” for against against converges.
In both cases the constant is uniquely determined and it applies . The advantage of this formulation is that it is easier to provide evidence as there is no need to consider a quotient. This representation of the best linear approximation was already consistently applied by Karl Weierstrass , Henri Cartan and Jean Dieudonné .
If a function is described as differentiable without referring to a specific point, then this means that it can be differentiated at every point in the domain, i.e. the existence of a clear tangent for every point on the graph.
Every differentiable function is continuous , but the converse is not true. At the beginning of the 19th century it was still believed that a continuous function could not be differentiated at most in a few places (like the absolute value function). Bernard Bolzano was the first mathematician to actually construct a function that is continuous everywhere, but nowhere differentiable, which, however, was not known in the professional world; Karl Weierstrass then also found such a function in the 1860s (see Weierstrass function ), which this time made waves among mathematicians. A well-known multidimensional example of a continuous, non-differentiable function is the Koch curve presented by Helge von Koch in 1904 .
Derivative function
The derivation of the function at the point marked with describes locally the behavior of the function in the vicinity of the point under consideration . Now it will not be the only place where it is differentiable. One can therefore try to assign the derivative at this point (i.e. ) to every number from the domain of definition . In this way a new function is obtained , the domain of which is the set of all places where it is differentiable. This function is called the derivative function or, for short, the derivative of and one says “ is differentiable”.
For example, the square function has the derivative at any point , so the square function is differentiable on the set of real numbers. The corresponding derivation function is given by .
The derivative function is usually different from the original, the only exception being the multiples of the exponential function .
If the derivative is continuous, then continuously is called continuously differentiable. Based on the designation for the totality (the space) of the continuous functions with a definition set , the space of the continuously differentiable functions is also abbreviated.
Derivative calculation
Computing the derivative of a function is called differentiation or differentiation ; in other words, one differentiates this function.
To find the derivative of elementary functions (eg. B. , ...) to calculate, it adheres closely to the above definition, explicitly calculated a difference quotient and then can go to zero. In school mathematics this is referred to as the "h method". The typical math user does this calculation only a few times in their life. Later he knows the derivatives of the most important elementary functions by heart, looks up derivatives of not so common functions in a set of tables (e.g. in the Bronstein-Semendjajew or our table of derivative and antiderivatives ) and calculates the derivative of composite functions with the help of the derivation rules .
Calculation of a derivative function
Find the derivation of . Then one calculates the difference quotient as
and receives the derivative of the function in the Limes
Non-differentiable function
is not differentiable at position 0:
For all applies namely and with it
- .
On the contrary, and consequently applies to all
- .
Since the left-hand and right-hand limit values do not match, the limit value does not exist. The function cannot therefore be differentiated at the point under consideration. The differentiability of the function in all other places is, however, still given.
However, the right-hand derivative exists at the 0 position
and the left-hand derivative
- .
If one looks at the graph of , one comes to the conclusion that the concept of differentiability clearly means that the associated graph runs without kinks.
A typical example of nowhere differentiable continuous functions, the existence of which seems difficult to imagine at first, are almost all paths of Brownian motion . This is used, for example, to model stock price charts .
Not continuously differentiable function
A function is called continuously differentiable if its derivative is continuous . Even if a function is differentiable everywhere, the derivative does not have to be continuous. For example is the function
at every point, inclusive , differentiable. The derivative, which can be determined at the point 0 via the difference quotient,
but is not continuous at 0.
Derivation rules
Derivatives of compound functions, e.g. B. or , one leads back to the differentiation of elementary functions with the help of derivation rules (see also: Table of derivation and antiderivatives ).
The following rules can be used to reduce the derivative of compound functions to derivatives of simpler functions. Let , and (in the domain of definition) be differentiable, real functions, and real numbers, then:
- Constant function
- Factor rule
- Sum rule
- Product rule
- Quotient rule
- Reciprocal rule
- Power rule
- Chain rule
- Reverse rule
- If a bijective function differentiable at this point is with , and its inverse function with differentiable, then the following applies:
- Reflected to a point of the graph of at the 1st bisector and therefor gets on , then the slope of in the reciprocal of the slope of in
- Logarithmic derivative
- From the chain rule it follows for the derivation of the natural logarithm of a function :
- A fraction of the shape is called a logarithmic derivative.
- Derivation of the power function
- To derive one remembers that powers with real exponents on the detour via the exponential function are defined: . Applying the chain rule and - for the inner derivative - the product rule results
- .
- Leibniz rule
- The derivation of -th order for a product of two -fold differentiable functions and results from
- .
- The expressions of the form appearing here are binomial coefficients .
- Formula by Faà di Bruno
- This formula enables the closed representation of the -th derivative of the composition of two -fold differentiable functions. It generalizes the chain rule to higher derivatives.
Geometric illustration of the derivation of the first polynomials
If the functions of the polynomials of the first, second and third degree are represented geometrically, the resulting derivation function is illustrated by creating a limit value.
A change of the parameter by any length causes a change in the function and results in the following:
- a line ( ) to a line change, which approximates for any small shifts from a point change in length ,
- of a square ( ) to a change in area, which for arbitrarily small shifts approaches a change by two distances in length ,
- of a cube ( ) to a change in volume, which for any small shift of a change by three areas approximates that of the area .

Treated more formally, the limit values can be determined based on the geometric considerations as follows:
Left column :
Shift by causing change in length (line 2):
For (line 3):
Limit value (line 4):
:
Middle column
Shift caused area change: (line 2):
For (line 3):
Thus the limit value (line 4) is:
Right column :
Shift caused volume change (line 2):
For (line 3):
Thus the limit value (line 4) is:
Central statements of differential calculus
Fundamental theorem of analysis
Leibniz's main achievement was the realization that integration and differentiation are related. He formulated this in the main theorem of differential and integral calculus, also called the fundamental theorem of analysis . It says:
If an interval, a continuous function and any point, then the function is
continuously differentiable, and their derivative is the same .
This gives instructions for integrating: We are looking for a function whose derivative is the integrand . Then:
Mean value theorem of differential calculus
Another central theorem of differential calculus is the mean value theorem , which was proven by Cauchy.
Let it be a function that is (with ) defined on the closed interval and is continuous. In addition, the function is differentiable in the open interval . Under these conditions there is at least one such that
applies.
Multiple derivatives
If the derivative of a function is again differentiable, the second derivative of can be defined as the derivative of the first. Third, fourth, etc. derivatives can then be defined in the same way. Accordingly, a function can be easily differentiable, double differentiable, etc.
The second derivative has numerous physical applications. For example, the first derivative of the location in terms of time is the instantaneous speed, the second derivative is the acceleration . The notation comes from physics , i.e. point of t , for derivatives of any function with respect to time.
When politicians comment on the "decline in the rise in the number of unemployed", they speak of the second derivative (change in the rise) in order to relativize the statement of the first derivative (rise in the number of unemployed).
Multiple derivatives can be written in three different ways:
or in the physical case (with a derivation according to time)
For the formal designation of any derivative one also defines and .
Notations
Historically, there are different notations to represent the derivative of a function.
Lagrange notation
So far in this article, the notation has mainly been used to derive from . This notation goes back to the mathematician Joseph-Louis Lagrange , who introduced it in 1797. With this notation, the second derivative of with and the -th derivative with is noted.
Newton notation
Isaac Newton - the founder of differential calculus alongside Leibniz - noted the first derivative of , and accordingly noted the second derivative through . Nowadays, this notation is mainly used in physics, especially mechanics , for the derivative with respect to time.
Leibniz notation
Gottfried Wilhelm Leibniz introduced the notation for the first derivation of (after the variable ) . This expression is read as " from to ". Leibniz noted for the second derivative and the -th derivative is noted with. Leibniz's spelling is not a fraction. The symbols and are called differentials , but have only a symbolic meaning in modern differential calculus (apart from the theory of differential forms ) and are only allowed in this notation as a formal differential quotient. In some applications ( chain rule , integration of some differential equations , integration through substitution ) one calculates with them almost as if they were ordinary variables.
Euler notation
The notation or for the first derivative of goes back to Leonhard Euler . In this notation, the second derivative is written by or and the -th derivative by or .
Applications
Minima and maxima
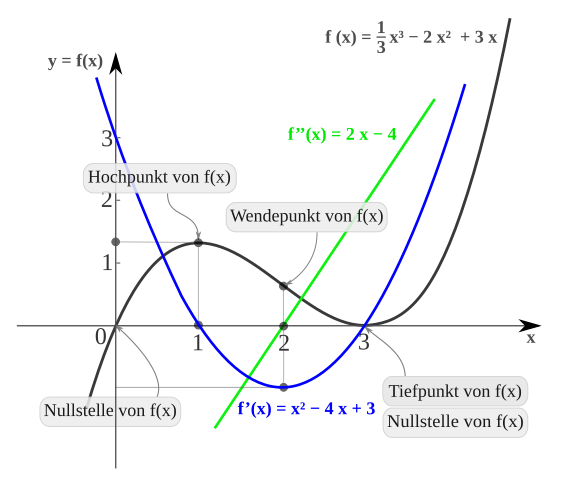
One of the most important applications of differential calculus is the determination of extreme values , mostly for the optimization of processes. In the case of monotonous functions , among other things, these are at the edge of the definition range, but generally at the points where the derivative is zero. A function can have a maximum or minimum value without the derivative existing at this point, but in the following only at least locally differentiable functions are considered. As an example we take the polynomial function with the function term
The figure shows the course of the graphs of , and .
Horizontal tangents
Has a function with one point its highest value, that applies to all of this interval , and is at the point differentiable, then the derivative there may be only equal to zero: . A corresponding statement applies if in assuming the smallest value.
The geometric interpretation of this Fermat theorem is that the graph of the function has a tangent running parallel to the -axis, also called a horizontal tangent, at local extreme points .
It is therefore a necessary condition for the existence of an extreme point for differentiable functions that the derivative takes the value 0 at the relevant point:
Conversely, the fact that the derivative has the value zero at one point cannot yet be used to infer an extreme point; a saddle point could also be present, for example . A list of various sufficient criteria, the fulfillment of which leads to an extreme point, can be found in the article Extreme value . These mostly use the second or even higher derivative.
Condition in the example
In the example is
It follows that exactly for and . The function values at these locations are and , i. H. the curve has horizontal tangents in the points and , and only in these.
Because the episode
consists of alternating small and large values, there must be a high and a low point in this area. According to Fermat's theorem, the curve has a horizontal tangent at these points, so only the points determined above come into question: So there is a high point and a low point.
Curve discussion
With the help of the derivations, further properties of the function can be analyzed, such as turning points , saddle point , convexity or the monotony already mentioned above . The implementation of these investigations is the subject of the curve discussion .
Taylor series and smoothness
If there is a ( ) times continuously differentiable function in the interval , then for all and out the representation of the so-called Taylor formula applies :
with the -th Taylor polynomial at the development point
and the ( ) th remainder
A function that can be differentiated any number of times is called a smooth function . Since it has all derivatives, the Taylor formula given above can be extended to the Taylor series of with expansion point
It turns out, however, that the existence of all derivatives does not mean that it can be represented by the Taylor series. In other words: every analytic function is smooth, but not the other way round, as the example of a non-analytic smooth function given in the article Taylor series shows.
The term is often found to be sufficiently smooth in mathematical considerations . This means that the function can be differentiated as often as necessary to carry out the current train of thought.
Differential equations
Another important application of differential calculus is the mathematical modeling of physical processes. Growth, movement or forces all have something to do with derivatives, so their formulaic description must contain differentials. This typically leads to equations in which derivatives of an unknown function appear, precisely differential equations .
For example, Newton's law of motion links
the acceleration of a body with its mass and the force acting on it . The basic problem of mechanics is therefore to infer the spatial function of a body from a given acceleration. This task, a reverse of twofold differentiation, has the mathematical form of a differential equation of the second order. The mathematical difficulty of this problem arises from the fact that location, velocity, and acceleration are vectors that generally do not point in the same direction, and that the force can be a function of time and location .
Since many models are multidimensional, the partial derivatives explained below, with which partial differential equations can be formulated , are often very important in the formulation. In a mathematically compact way, these are described and analyzed using differential operators .
Differential calculus as a calculus
In addition to determining the slope of functions, differential calculus is an essential aid in term transformation thanks to its calculus . Here one breaks away from any connection with the original meaning of the derivative as an increase. If two terms have been recognized as the same, further (sought) identities can be obtained from them by differentiation. An example may make this clear:
From the telescope sum
should
can be obtained as easily as possible. This is achieved by differentiation using the quotient rule :
Alternatively, the identity can also be obtained by multiplying and then telescoping it three times , but this is not so easy to see through .
Complex differentiability
So far only real functions have been spoken of. For differentiability of functions with complex arguments, the definition with linearization is simply used. Here the condition is much more restrictive than in the real one: For example, the absolute value function is nowhere complex to differentiate. At the same time, every function that is complexly differentiable in an environment is automatically differentiable as often as required, so all higher derivatives exist.
Derivatives of multidimensional functions
All previous explanations were based on a function in a variable (i.e. with a real or complex number as an argument). Functions that map vectors to vectors or vectors to numbers can also have a derivative. However, a tangent to the function graph is no longer uniquely determined in these cases, as there are many different directions. An expansion of the previous term of derivation is therefore necessary here.
Partial derivatives
We first consider a function that goes from. An example is the temperature function : depending on the location, the temperature in the room is measured in order to assess how effective the heating is. If the thermometer is moved in a certain direction, a change in temperature can be observed. This corresponds to the so-called directional derivation . The directional derivatives in special directions, namely those of the coordinate axes, are called the partial derivatives.
Overall, partial derivatives can be calculated for a function in variables :
The individual partial derivatives of a function can also be bundled as a gradient or nablavector . Partial derivatives can again be differentiable and their partial derivatives can then be arranged in the so-called Hessian matrix . Analogous to the one-dimensional case, the candidates for local extreme points are where the derivative is zero, i.e. the gradient disappears. Likewise, the second derivative, i.e. the Hessian matrix, determines the exact case in certain cases. In contrast to the one-dimensional, however, the variety of shapes is greater in this case. The different cases can be classified by means of a principal axis transformation of the quadratic form given by a multidimensional Taylor expansion in the point under consideration .
Example of applied differential calculus
In microeconomics , for example, different types of production functions are analyzed in order to gain insights into macroeconomic relationships. The typical behavior of a production function is of particular interest here: How does the dependent variable output (e.g. output of an economy) react when the input factors (here: labor and capital ) are increased by an (infinitesimal) small unit?
A basic type of a production function is the neoclassical production function . It is characterized, among other things, by the fact that the output increases with every additional input, but that the increases are decreasing. For example, it is the production function for an economy
With
authoritative. At any point in time, output is produced in the economy using the production factors labor and capital with the help of a given level of technology . The first derivation of this function according to the factors of production gives:
Since the partial derivatives can only be positive due to the restriction , you can see that the output rises when the respective input factors increase. The partial derivatives of the 2nd order give:
They will be negative for all inputs, so the growth rates will fall. So you could say that if the input rises, the output rises below proportionally . The relative change in output in relation to a relative change in input is given here by the elasticity . In the present case, the production elasticity of capital denotes , which in this production function corresponds to the exponent , which in turn represents the capital income ratio. Consequently, with an (infinitesimal) small increase in capital, output increases by the capital income ratio.
Implicit differentiation
If a function is given by an implicit equation , it follows from the multidimensional chain rule that applies to functions of several variables
The derivation of the function therefore results in
- With
Total differentiability
A function , where is an open set , is called totally differentiable (or only differentiable) at a point , if a linear mapping exists such that
- applies.
For the one-dimensional case, this definition agrees with the one given above. The linear mapping is uniquely determined if it exists, so it is in particular independent of the choice of equivalent norms . The tangent is thus abstracted through the local linearization of the function. The matrix representation of the first derivative of is called the Jacobi matrix . It is a matrix. The gradient described above is obtained for.
The following relationship exists between the partial derivatives and the total derivative: If the total derivative exists at a point, then all partial derivatives also exist there. In this case, the partial derivatives agree with the coefficients of the Jacobian matrix. Conversely, the existence of the partial derivatives does not necessarily result in total differentiability, not even continuity. However, if the partial derivatives are also in a neighborhood of continuous , then the function in is also totally differentiable.
Important sentences
- Schwarz's theorem : The order of differentiation is irrelevant when calculating partial derivatives of higher order if all partial derivatives up to and including this order are continuous.
- Theorem of the implicit function : Function equations are solvable if the Jacobi matrix is locally invertible with respect to certain variables.
Generalizations and Related Areas
- In many applications it is desirable to be able to generate derivatives for continuous or even discontinuous functions. For example, a wave breaking on the beach can be modeled by a partial differential equation, but the function of the height of the wave is not even continuous. To this end, in the middle of the 20th century, the term “derivative” was generalized to the area of distributions , where a weak derivative was defined . Closely related to this is the concept of the Sobolev space .
- In the differential geometry of curved surfaces are examined. The term differential form is required for this.
- The term derivation as linearization can be applied analogously to functions between two normed topological vector spaces and ( see main article Fréchet derivation , Gâteaux differential , Lorch derivation ): then in Fréchet is called differentiable if a continuous linear operator exists, so that
- .
- A transfer of the concept of derivation to rings other than and (and algebras above) is derivation .
- The difference calculation transfers the differential calculation to series .
literature
Differential calculus is a central subject in the upper secondary level and is therefore dealt with in all mathematics textbooks at this level.
Textbooks for math students
- Henri Cartan : Differential Calculus. Bibliographisches Institut, Mannheim 1974, ISBN 3-411-01442-3 .
- Henri Cartan : Differential Forms. Bibliographisches Institut, Mannheim 1974, ISBN 3-411-01443-1 .
- Henri Cartan : Elementary Theories of the Analytical Functions of One and Several Complex Variables. Bibliographisches Institut, Mannheim 1966, 1981, ISBN 3-411-00112-7 .
- Richard Courant : Lectures on differential and integral calculus. 2 volumes. Springer 1928, 4th edition 1971, ISBN 3-540-02956-7 .
- Jean Dieudonné : Fundamentals of modern analysis. Volume 1. Vieweg, Braunschweig 1972, ISBN 3-528-18290-3 .
- Gregor M. Fichtenholz : differential and integral calculus I – III. Harri Deutsch publishing house, Frankfurt am Main 1990-2004, ISBN 978-3-8171-1418-4 (complete set).
- Otto Forster : Analysis 1. Differential and integral calculus of a variable. 7th edition. Vieweg, Braunschweig 2004, ISBN 3-528-67224-2 .
- Otto Forster: Analysis 2. Differential calculus im . Ordinary differential equations. 6th edition. Vieweg, Braunschweig 2005, ISBN 3-528-47231-6 .
- Konrad Königsberger : Analysis. 2 volumes. Springer, Berlin 2004, ISBN 3-540-41282-4 .
- Vladimir I. Smirnov : Course in Higher Mathematics (Part 1–5). Harri Deutsch publishing house, Frankfurt am Main, 1995-2004, ISBN 978-3-8171-1419-1 (complete set).
- Steffen Timmann: Review of Analysis. 2 volumes. Binomi, Springe 1993, ISBN 3-923923-50-3 , ISBN 3-923923-52-X .
Textbooks for the basic subject of mathematics
- Rainer Ansorge, Hans Joachim Oberle: Mathematics for engineers. Volume 1. Akademie-Verlag, Berlin 1994, 3rd edition 2000, ISBN 3-527-40309-4 .
- Günter Bärwolff (with the assistance of G. Seifert): Higher mathematics for natural scientists and engineers. Elsevier Spektrum Akademischer Verlag, Munich 2006, ISBN 3-8274-1688-4 .
- Lothar Papula : Mathematics for natural scientists and engineers. Volume 1. Vieweg, Wiesbaden 2004, ISBN 3-528-44355-3 .
- Klaus Weltner: Mathematics for Physicists. Volume 1. Springer, Berlin 2006, ISBN 3-540-29842-8 .
- Peter Dörsam: Mathematics clearly presented for students of economics. 15th edition. PD-Verlag, Heidenau 2010, ISBN 978-3-86707-015-7 .
Web links
- Tool for the determination of derivatives of any function with one or more variables with calculation path (German; requires JavaScript)
- Online calculator for deriving functions with calculation method and explanations (German)
- Tool for the determination of derivatives and primitives of functions with a variable (English)
- Basic idea of differentiation - film clip
- Clear explanation of derivations
- Examples for each derivation rule
Individual evidence
- ^ Hans Wussing, Heinz-Wilhelm Alten, Heiko Wesemüller-Kock, Eberhard Zeidler: 6000 years of mathematics: From the beginnings to Newton and Leibniz. Springer-Verlag 2008, p. 427/428.
- ^ Hans Wussing, Heinz-Wilhelm Alten, Heiko Wesemüller-Kock, Eberhard Zeidler: 6000 years of mathematics: From Euler to the present. Springer-Verlag 2008, p. 233.
- ↑ differential calculus . In: Guido Walz (Ed.): Lexicon of Mathematics . 1st edition. Spectrum Academic Publishing House, Mannheim / Heidelberg 2000, ISBN 3-8274-0439-8 .






























































































































![f \ colon [a, b] \ to \ mathbb {R}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c5ab61178bf5349838758ffe3d96135406ed0245)
![[from]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)