Mean value theorem of differential calculus
The mean value theorem is a central principle of differential calculus , a branch of analysis ( mathematics ). Illustrated, the mean value theorem can be interpreted geometrically in such a way that, under the conditions mentioned below, there is at least one curve point between two points of a function graph for which the tangent is parallel to the secant through the two given points. The secant slope between two points is thus assumed as the tangent slope by the function at least once.
Global properties that can be expressed with the help of the secant slope can thus be traced back to properties of the derivative with the help of the mean value theorem. Examples of this are de l'Hospital's rule or various sentences about the discussion of curves (such as the sentence that functions with a positive derivative grow strictly monotonically). The statement of the theorem can be applied to the quotient of two functions as well as to functions of several variables. The mean theorem generalizes the theorem of Rolle .
The theorem was first proved by Joseph-Louis Lagrange (Théorie des fonctions analytiques 1797) and later by Augustin Louis Cauchy (Lectures on calculus, Calcul infinitésimal, 1823). Pierre Ossian Bonnet proved the mean value theorem from Rolle's theorem (presented in Serret's lectures on calculus, 1868).
Statement of the mean value theorem
Let it be a function that is (with ) defined on the closed interval and is continuous . In addition, the function is differentiable in the open interval . Under these conditions there is at least one such that
applies. Interpreted geometrically, this means that the secant slope occurs at at least one point between and as the slope of the tangent on the function graph.
Proof in the one-dimensional case
Let an auxiliary function be defined with
is continuously differentiable in and in . It applies .
According to the principle of role there is therefore a with . There
follows the claim.
Example of an application of the mean value theorem
As a typical application of the mean value theorem, it can be shown that
The following applies to everyone : We can accept without restriction . Since the sine function can be differentiated in the interval , there exists according to the mean value theorem such that
applies. Because of for all , one receives
In general, it can be shown that continuously differentiable functions are locally Lipschitz continuous .
Extended mean value theorem of differential calculus
The mean value theorem can be generalized in the following way:
Let and be two functions that are (with ) defined on the closed interval and are continuous and differentiable on the open interval . Under these conditions there is at least one such that
applies.
If, in addition , the interval is assumed, then in particular as well as and the extended mean value theorem can be written in the usual fraction form,
- .
proof
If , then for the generalized mean value theorem of differential calculus it must be shown that the following holds true for a
- .
According to the principle of role, there is one to which applies.
Is , so you can function
define on the interval . Since , it indicates to the set of a role with so
- .
By rearranging this equation, the claim follows.
Mean value theorem for real-valued functions of several variables
In multidimensional analysis, the mean value theorem is as follows:
Let it be a mapping with , further be differentiable on an open, convex set . Also be with . Then there is at least one with and and the following applies:
For the theorem corresponds to the above mentioned mean value theorem of the one-dimensional differential calculus. denotes the gradient at the point that occurs in a scalar product .
Interpreted geometrically, the secant gradient occurs between and at at least one point from as a gradient in the direction of the vector .
Proof in the multidimensional case
Looking at the function with
- ,
so is steady on and differentiable on . Thus it follows from the mean value theorem of one-dimensional analysis that one exists such that
- .
From the chain rule it now follows:
- .
This can be summarized as follows:
If you now substitute by , it results
- ,
with which the statement of the theorem would be proven.
Mean value theorem for vector-valued functions of several variables
An expansion of the set to include functions is only possible under changed geometrical conditions or tightening. In particular, the set of linear mappings in question is expanded considerably beyond the derivatives on the route :
If the derivatives of are restricted to the entire segment (they are Jacobian matrices , i.e. restricted with respect to a norm to , for example the operator norm ), there is a linear mapping from the closed convex hull of the derivatives on the connecting segment, so that
applies.
The proof for this takes place via the main theorem of differential and integral calculus on the auxiliary functions . Why the derivatives on the route are not sufficient can be understood as follows: On the one hand, the mean value theorem for real-valued functions of several variables can be applied to the individual components of the vector-valued function . On the other hand, it is by no means guaranteed that the associated point at which the suitable derivative is found is the same for all component functions. So you have to look around in a larger amount, namely the convex hull of the derivatives on the route.
Illustrative meaning
For example, if the function describes a distance as a function of time, the derivative is the speed. The mean value theorem then says: On the way from A to B you have to have been as fast as your average speed at least at one point in time.
Conclusions from the mean value theorem
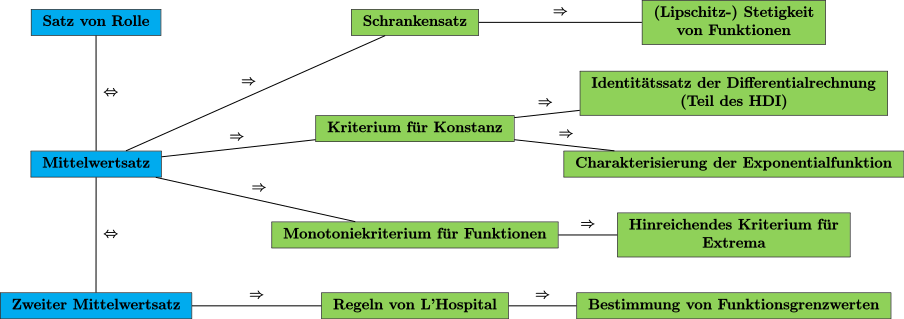
The following results of analysis can be proven from the mean theorem:
- The barrier theorem can be proven from the mean theorem. This means that for continuous functions that are differentiable with a limited derivative, the inequality for a holds. You can choose . With this, the Lipschitz continuity of numerous functions can be proven.
- Another consequence is the criterion for constancy. This says that a function is constant if is (the derivative is constant zero). With this we can derive the identity theorem of differential calculus . This states that two functions with an identical derivative only differ by one constant. It is an essential part of the main theorem of differential and integral calculus. Another consequence of the criterion for constancy is the characterization of the exponential function via the differential equation .
- The monotony criterion for differentiable functions can also be proven with the mean value theorem. This creates a connection between the monotonic behavior of the function and the sign of the derivative function. More precisely, it is monotonically rising (or falling) if and only if (or ) is. From this one can derive a sufficient criterion for the existence of an extremum of a function at a point.
- From the second mean theorem (better known as the extended mean theorem ), L'Hospital's rules can be inferred. With their help, numerous limit values of quotients of two functions can be calculated with the help of the derivative.
The points listed are summarized in the following overview diagram:
See also
literature
- Otto Forster : Analysis 1. Differential and integral calculus of a variable . 8th edition. Vieweg-Verlag, 2006, ISBN 3-528-67224-2
- Otto Forster : Analysis 2. Differential calculus in R n . Ordinary differential equations . 7th edition. Vieweg-Verlag, 2006, ISBN 3-528-47231-6
- Konrad Königsberger : Analysis 1 . Springer, Berlin 2004, ISBN 3-540-41282-4
- Konrad Königsberger : Analysis 2 . Springer-Verlag, Berlin / Heidelberg, 2000, ISBN 3-540-43580-8
Web links
Individual evidence
- ↑ Florian Cajori: On Michel Rolle's book "Méthode pour resoudre les égalitez" and the history of Rolle's theorem . In: Bibliotheca Mathematica , 1911, p. 310
- ↑ mathepedia.de










![{\ displaystyle f \ colon [a, b] \ to \ mathbb {R}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c5ab61178bf5349838758ffe3d96135406ed0245)
![[from]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)





![{\ displaystyle h \ colon [a, b] \ to \ mathbb {R}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b46ce7569c8ce5a8b5996b1f85c91c374dcd8617)











![{\ displaystyle g \ colon [a, b] \ to \ mathbb {R}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/38132af5ea7cd916293fe93f29187bd461a5e270)




























![{\ displaystyle h \ colon [0,1] \ to \ mathbb {R}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/838110915942de3de912b09350bcbd6c7e06d8d2)

![[0.1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)