Scalar product

This article covers the multiplication of two vectors, the result of which is a scalar . For the multiplication of vectors by scalars, the result of which is a vector, see scalar multiplication .

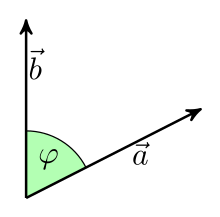
The scalar product of two vectors in Euclidean intuition space depends on the length of the vectors and the included angle.

The scalar product (also inner product or point product ) is a mathematical combination that assigns a number ( scalar ) to two vectors . It is the subject of analytical geometry and linear algebra . Historically, it was first introduced in Euclidean space . Geometrically calculating the scalar product of two vectors and according to the formula ${\displaystyle {\vec {a}}}$ ${\displaystyle {\vec {b}}}$

${\displaystyle {\vec {a}}\cdot {\vec {b}}=|{\vec {a}}|\,|{\vec {b}}|\,\cos \sphericalangle ({\vec {a}},{\vec {b}}).}$

And denote the lengths (amounts) of the vectors. With is the cosine of the angle enclosed by the two vectors . The scalar product of two vectors of a given length is therefore zero if they are perpendicular to one another and maximum if they have the same direction. ${\displaystyle |{\vec {a}}|}$ ${\displaystyle |{\vec {b}}|}$ ${\displaystyle \cos \sphericalangle ({\vec {a}},{\vec {b}})=\cos \varphi }$ ${\displaystyle \varphi }$

In a Cartesian coordinate system , the scalar product of two vectors and is calculated as ${\displaystyle {\vec {a}}=(a_{1},a_{2},a_{3})}$ ${\displaystyle {\vec {b}}=(b_{1},b_{2},b_{3})}$

${\displaystyle {\vec {a}}\cdot {\vec {b}}=a_{1}\,b_{1}+a_{2}\,b_{2}+a_{3}\,b_{3}.}$

If you know the Cartesian coordinates of the vectors, you can use this formula to calculate the scalar product and then use the formula from the previous paragraph to calculate the angle between the two vectors by solving it for : ${\displaystyle \varphi =\sphericalangle ({\vec {a}},{\vec {b}})}$ ${\displaystyle \varphi }$

${\displaystyle \varphi =\arccos {\frac {{\vec {a}}\cdot {\vec {b}}}{|{\vec {a}}||{\vec {b}}|}}}$

In linear algebra, this concept is generalized. A scalar product is a function that assigns a scalar to two elements of a real or complex vector space , more precisely a ( positively definite ) Hermitian sesquilinear form , or more specifically in real vector spaces a (positively definite) symmetrical bilinear form . In general, no scalar product is defined from the start in a vector space. A space together with a scalar product is called an interior product space or a prehilbert space . These vector spaces generalize Euclidean space and thus enable the application of geometric methods to abstract structures.

In Euclidean space

Geometric definition and notation

Vectors in three-dimensional Euclidean space or in the two-dimensional Euclidean plane can be represented as arrows. In this case, filters arrows parallel have the same length oriented, and equal to, the same vector. The dot product of two vectors , and is a scalar, that is a real number. Geometrically, it can be defined as follows: ${\displaystyle {\vec {a}}\cdot {\vec {b}}}$ ${\displaystyle {\vec {a}}}$ ${\displaystyle {\vec {b}}}$

And denote the lengths of the vectors and and denotes the angle enclosed by and , so is ${\displaystyle a=|{\vec {a}}|}$ ${\displaystyle b=|{\vec {b}}|}$ ${\displaystyle {\vec {a}}}$ ${\displaystyle {\vec {b}}}$ ${\displaystyle \varphi =\sphericalangle ({\vec {a}},{\vec {b}})}$ ${\displaystyle {\vec {a}}}$ ${\displaystyle {\vec {b}}}$

${\displaystyle {\vec {a}}\cdot {\vec {b}}=|{\vec {a}}|\,|{\vec {b}}|\,\cos \sphericalangle ({\vec {a}},{\vec {b}})=a\,b\,\cos \varphi .}$

As with normal multiplication (but less often than there), when it is clear what is meant, the multiplication sign is sometimes left out:

${\displaystyle {\vec {a}}\cdot {\vec {b}}={\vec {a}}\,{\vec {b}}}$

Instead of writing occasionally in this case ${\displaystyle {\vec {a}}\cdot {\vec {a}}}$ ${\displaystyle {\vec {a}}\,^{2}.}$

Other common notations are and ${\displaystyle {\vec {a}}\circ {\vec {b}},\ {\vec {a}}\bullet {\vec {b}}}$ ${\displaystyle \langle {\vec {a}},{\vec {b}}\rangle .}$

illustration

Orthogonal projection of the vector on the direction determined by ${\displaystyle {\vec {b}}_{\vec {a}}}$ ${\displaystyle {\vec {b}}}$ ${\displaystyle {\vec {a}}}$

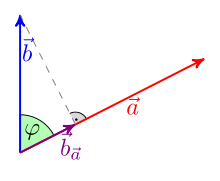
To illustrate the definition, consider the orthogonal projection of the vector on the direction given by and set ${\displaystyle {\vec {b}}_{\vec {a}}}$ ${\displaystyle {\vec {b}}}$ ${\displaystyle {\vec {a}}}$

${\displaystyle b_{a}={\begin{cases}|{\vec {b}}_{\vec {a}}|&{\text{falls }}{\vec {a}},{\vec {b}}_{\vec {a}}{\text{ gleichorientiert}}\\-|{\vec {b}}_{\vec {a}}|&{\text{falls }}{\vec {a}},{\vec {b}}_{\vec {a}}{\text{ entgegengesetzt orientiert}}\end{cases}}}$

Then and for the scalar product of and we have: ${\displaystyle b_{a}=b\cos \varphi }$ ${\displaystyle {\vec {a}}}$ ${\displaystyle {\vec {b}}}$

${\displaystyle {\vec {a}}\cdot {\vec {b}}=ab_{a}}$

This relationship is sometimes used to define the scalar product.

Examples

In all three examples, and . The scalar products result from the special cosine values , and : ${\displaystyle |{\vec {a}}|=5}$ ${\displaystyle |{\vec {b}}|=3}$ ${\displaystyle \cos 0^{\circ }=1}$ ${\displaystyle \cos 60^{\circ }={\tfrac {1}{2}}}$ ${\displaystyle \cos 90^{\circ }=0}$

• 

  ${\displaystyle {\vec {a}}}$and rectified ${\displaystyle {\vec {b}}}$
  ${\displaystyle {\vec {a}}\cdot {\vec {b}}=5\cdot 3\cdot \cos 0^{\circ }=15}$

• 

  ${\displaystyle {\vec {a}}}$and at a 60 ° angle ${\displaystyle {\vec {b}}}$
  ${\displaystyle {\vec {a}}\cdot {\vec {b}}=5\cdot 3\cdot \cos 60^{\circ }=7{,}5}$

• 

  ${\displaystyle {\vec {a}}}$and orthogonal ${\displaystyle {\vec {b}}}$
  ${\displaystyle {\vec {a}}\cdot {\vec {b}}=5\cdot 3\cdot \cos 90^{\circ }=0}$

In Cartesian coordinates

If you introduce Cartesian coordinates in the Euclidean plane or in Euclidean space, each vector has a coordinate representation as a 2- or 3-tuple, which is usually written as a column.

In the Euclidean plane one then obtains the scalar product of the vectors

${\displaystyle {\vec {a}}={\begin{pmatrix}a_{1}\\a_{2}\end{pmatrix}}}$  and   ${\displaystyle {\vec {b}}={\begin{pmatrix}b_{1}\\b_{2}\end{pmatrix}}}$

the representation

${\displaystyle {\vec {a}}\cdot {\vec {b}}={\begin{pmatrix}a_{1}\\a_{2}\end{pmatrix}}\cdot {\begin{pmatrix}b_{1}\\b_{2}\end{pmatrix}}=a_{1}b_{1}+a_{2}b_{2}.}$

Canonical unit vectors in the Euclidean plane

For the canonical unit vectors and the following applies: ${\displaystyle {\vec {e}}_{1}={\begin{pmatrix}1\\0\end{pmatrix}}}$ ${\displaystyle {\vec {e}}_{2}={\begin{pmatrix}0\\1\end{pmatrix}}}$

${\displaystyle {\vec {e}}_{1}\cdot {\vec {e}}_{1}=1,\ {\vec {e}}_{1}\cdot {\vec {e}}_{2}={\vec {e}}_{2}\cdot {\vec {e}}_{1}=0}$ and ${\displaystyle {\vec {e}}_{2}\cdot {\vec {e}}_{2}=1}$

It follows from this (anticipating the properties of the scalar product explained below):

${\displaystyle {\begin{aligned}{\vec {a}}\cdot {\vec {b}}&=(a_{1}\,{\vec {e}}_{1}+a_{2}\,{\vec {e}}_{2})\cdot (b_{1}\,{\vec {e}}_{1}+b_{2}\,{\vec {e}}_{2})\\&=a_{1}b_{1}\,{\vec {e}}_{1}\cdot {\vec {e}}_{1}+a_{1}b_{2}\,{\vec {e}}_{1}\cdot {\vec {e}}_{2}+a_{2}b_{1}\,{\vec {e}}_{2}\cdot {\vec {e}}_{1}+a_{2}b_{2}\,{\vec {e}}_{2}\cdot {\vec {e}}_{2}\\&=a_{1}b_{1}+a_{2}b_{2}\end{aligned}}}$

In three-dimensional Euclidean space one obtains correspondingly for the vectors

${\displaystyle {\vec {a}}={\begin{pmatrix}a_{1}\\a_{2}\\a_{3}\end{pmatrix}}}$  and   ${\displaystyle {\vec {b}}={\begin{pmatrix}b_{1}\\b_{2}\\b_{3}\end{pmatrix}}}$

the representation

${\displaystyle {\vec {a}}\cdot {\vec {b}}={\begin{pmatrix}a_{1}\\a_{2}\\a_{3}\end{pmatrix}}\cdot {\begin{pmatrix}b_{1}\\b_{2}\\b_{3}\end{pmatrix}}=a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}.}$

For example, the scalar product of the two vectors is calculated

${\displaystyle {\vec {a}}={\begin{pmatrix}1\\2\\3\end{pmatrix}}}$  and   ${\displaystyle {\vec {b}}={\begin{pmatrix}-7\\8\\9\end{pmatrix}}}$

as follows:

${\displaystyle {\vec {a}}\cdot {\vec {b}}=1\cdot (-7)+2\cdot 8+3\cdot 9=36}$

properties

From the geometric definition it follows directly:

• If and are parallel and equally oriented ( ), then applies ${\displaystyle {\vec {a}}}$ ${\displaystyle {\vec {b}}}$ ${\displaystyle \varphi =0^{\circ }}$

  ${\displaystyle {\vec {a}}\cdot {\vec {b}}=ab.}$

• In particular, the scalar product of a vector with itself is the square of its length:

  ${\displaystyle {\vec {a}}\cdot {\vec {a}}=a^{2}}$

• If and are oriented parallel and opposite ( ), then applies ${\displaystyle {\vec {a}}}$ ${\displaystyle {\vec {b}}}$ ${\displaystyle \varphi =180^{\circ }}$

  ${\displaystyle {\vec {a}}\cdot {\vec {b}}=-ab.}$

• If and are orthogonal ( ), then ${\displaystyle {\vec {a}}}$ ${\displaystyle {\vec {b}}}$ ${\displaystyle \varphi =90^{\circ }}$

  ${\displaystyle {\vec {a}}\cdot {\vec {b}}=0.}$

• If there is an acute angle, then the following applies ${\displaystyle \sphericalangle ({\vec {a}},{\vec {b}})}$ ${\displaystyle {\vec {a}}\cdot {\vec {b}}>0.}$
• Is an obtuse angle , the following applies ${\displaystyle \sphericalangle ({\vec {a}},{\vec {b}})}$ ${\displaystyle {\vec {a}}\cdot {\vec {b}}<0.}$

As a function that assigns the real number to every ordered pair of vectors , the scalar product has the following properties that one expects from a multiplication: ${\displaystyle ({\vec {a}},{\vec {b}})}$ ${\displaystyle {\vec {a}}\cdot {\vec {b}}}$

1. It is symmetrical (commutative law):

   ${\displaystyle {\vec {a}}\cdot {\vec {b}}={\vec {b}}\cdot {\vec {a}}}$for all vectors and ${\displaystyle {\vec {a}}}$ ${\displaystyle {\vec {b}}}$

2. It is homogeneous in every argument (mixed associative law):

   ${\displaystyle (r{\vec {a}})\cdot {\vec {b}}=r\,({\vec {a}}\cdot {\vec {b}})={\vec {a}}\cdot (r{\vec {b}})}$for all vectors and and all scalars ${\displaystyle {\vec {a}}}$ ${\displaystyle {\vec {b}}}$ ${\displaystyle r\in \mathbb {R} }$

3. It is additive in every argument (distributive law):

   ${\displaystyle {\vec {a}}\cdot ({\vec {b}}+{\vec {c}})={\vec {a}}\cdot {\vec {b}}+{\vec {a}}\cdot {\vec {c}}}$ and

   ${\displaystyle ({\vec {a}}+{\vec {b}})\cdot {\vec {c}}={\vec {a}}\cdot {\vec {c}}+{\vec {b}}\cdot {\vec {c}}}$for all vectors and ${\displaystyle {\vec {a}},}$ ${\displaystyle {\vec {b}}}$ ${\displaystyle {\vec {c}}.}$

Properties 2 and 3 are also summarized: The scalar product is bilinear .

The designation "mixed associative law" for the 2nd property makes it clear that a scalar and two vectors are linked in such a way that the brackets can be exchanged as in the associative law. Since the scalar product is not an inner link, a scalar product of three vectors is not defined, so the question of real associativity does not arise. In the expression , only the first multiplication is a scalar product of two vectors, the second is the product of a scalar with a vector ( S multiplication ). The expression represents a vector, a multiple of the vector On the other hand, the expression represents a multiple of . In general, then, ${\displaystyle ({\vec {a}}\cdot {\vec {b}})\,{\vec {c}}}$ ${\displaystyle {\vec {c}}.}$ ${\displaystyle {\vec {a}}\,({\vec {b}}\cdot {\vec {c}})}$ ${\displaystyle {\vec {a}}}$

${\displaystyle ({\vec {a}}\cdot {\vec {b}})\,{\vec {c}}\neq {\vec {a}}\,({\vec {b}}\cdot {\vec {c}}).}$

Neither the geometric definition nor the definition in Cartesian coordinates is arbitrary. Both follow from the geometrically motivated requirement that the scalar product of a vector with itself is the square of its length, and the algebraically motivated requirement that the scalar product fulfills the above properties 1-3.

Amount of vectors and included angles

With the help of the scalar product it is possible to calculate the length (the amount) of a vector from the coordinate representation:

The following applies to a vector of two-dimensional space ${\displaystyle {\vec {a}}={\begin{pmatrix}a_{1}\\a_{2}\end{pmatrix}}}$

${\displaystyle |{\vec {a}}|={\sqrt {{\vec {a}}\cdot {\vec {a}}}}={\sqrt {{a_{1}}^{2}+{a_{2}}^{2}}}.}$

You can recognize the Pythagorean theorem here . The same applies in three-dimensional space

${\displaystyle |{\vec {a}}|={\sqrt {{\vec {a}}\cdot {\vec {a}}}}={\sqrt {{a_{1}}^{2}+{a_{2}}^{2}+{a_{3}}^{2}}}.}$

By combining the geometric definition with the coordinate representation, the angle they enclose can be calculated from the coordinates of two vectors. Out

${\displaystyle {\vec {a}}\cdot {\vec {b}}=|{\vec {a}}|\,|{\vec {b}}|\,\cos \sphericalangle ({\vec {a}},{\vec {b}})}$

follows

${\displaystyle \cos \sphericalangle ({\vec {a}},{\vec {b}})={\frac {{\vec {a}}\cdot {\vec {b}}}{|{\vec {a}}|\,|{\vec {b}}|}}.}$

The lengths of the two vectors

${\displaystyle {\vec {a}}={\begin{pmatrix}1\\2\\3\end{pmatrix}}}$  and   ${\displaystyle {\vec {b}}={\begin{pmatrix}-7\\8\\9\end{pmatrix}}}$

so amount

${\displaystyle |{\vec {a}}|={\sqrt {1^{2}+2^{2}+3^{2}}}={\sqrt {14}}\approx 3{,}74}$ and ${\displaystyle |{\vec {b}}|={\sqrt {(-7)^{2}+8^{2}+9^{2}}}={\sqrt {194}}\approx 13{,}93.}$

The cosine of the angle enclosed by the two vectors is calculated as

${\displaystyle \cos \sphericalangle ({\vec {a}},{\vec {b}})={\frac {36}{{\sqrt {14}}\cdot {\sqrt {194}}}}\approx 0{,}691.}$

So is ${\displaystyle \sphericalangle ({\vec {a}},{\vec {b}})\approx 46{,}3^{\circ }.}$

Orthogonality and Orthogonal Projection

→ Main articles : Orthogonality  and orthogonality projection

Orthogonal projection of the vector on the direction determined by ${\displaystyle {\vec {b}}_{\vec {a}}}$ ${\displaystyle {\vec {b}}}$ ${\displaystyle {\vec {a}}}$

Two vectors and are orthogonal if and only if their scalar product is zero, that is ${\displaystyle {\vec {a}}}$ ${\displaystyle {\vec {b}}}$

${\displaystyle {\vec {a}}\perp {\vec {b}}\iff {\vec {a}}\cdot {\vec {b}}=0.}$

The orthogonal projection from onto the direction given by the vector is the vector with ${\displaystyle {\vec {b}}}$ ${\displaystyle {\vec {a}}}$ ${\displaystyle {\vec {b}}_{\vec {a}}=k{\vec {a}}}$

${\displaystyle k={\frac {{\vec {b}}\cdot {\vec {a}}}{{\vec {a}}\cdot {\vec {a}}}}={\frac {{\vec {b}}\cdot {\vec {a}}}{|{\vec {a}}|^{2}}},}$

so

${\displaystyle {\vec {b}}_{\vec {a}}={\frac {{\vec {b}}\cdot {\vec {a}}}{|{\vec {a}}|^{2}}}\,{\vec {a}}=\left({\vec {b}}\cdot {\frac {\vec {a}}{|{\vec {a}}|}}\right)\,{\frac {\vec {a}}{|{\vec {a}}|}}.}$

The projection is the vector whose end point is the plumb line from the end point of to the straight line through the zero point determined by. The vector is vertical ${\displaystyle {\vec {b}}}$ ${\displaystyle {\vec {a}}}$ ${\displaystyle {\vec {b}}-{\vec {b}}_{\vec {a}}}$ ${\displaystyle {\vec {a}}.}$

If a unit vector (i.e., ist ), the formula simplifies to ${\displaystyle {\vec {a}}}$ ${\displaystyle |{\vec {a}}|=1}$

${\displaystyle {\vec {b}}_{\vec {a}}=({\vec {b}}\cdot {\vec {a}})\,{\vec {a}}.}$

Relation to the cross product

Another way of combining two vectors and multiplying them in three-dimensional space is the outer product or cross product. In contrast to the scalar product, the result of the cross product is not a scalar, but a vector again. This vector is perpendicular to the plane spanned by the two vectors and and its length corresponds to the area of the parallelogram that is spanned by them. ${\displaystyle {\vec {a}}}$ ${\displaystyle {\vec {b}}}$ ${\displaystyle {\vec {a}}\times {\vec {b}}.}$ ${\displaystyle {\vec {a}}}$ ${\displaystyle {\vec {b}}}$

The following calculation rules apply to the connection of the cross product and the scalar product:

• ${\displaystyle ({\vec {a}}\times {\vec {b}})\cdot {\vec {c}}={\vec {a}}\cdot ({\vec {b}}\times {\vec {c}})}$
• ${\displaystyle ({\vec {a}}\times {\vec {b}})\cdot {\vec {c}}=-({\vec {b}}\times {\vec {a}})\cdot {\vec {c}}}$
• ${\displaystyle ({\vec {a}}\times {\vec {b}})\cdot {\vec {a}}=({\vec {a}}\times {\vec {b}})\cdot {\vec {b}}=0}$
• ${\displaystyle ({\vec {a}}\times {\vec {b}})\cdot ({\vec {a}}\times {\vec {b}})=({\vec {a}}\cdot {\vec {a}})({\vec {b}}\cdot {\vec {b}})-({\vec {a}}\cdot {\vec {b}})^{2}}$

The combination of the cross product and the scalar product of the first two rules is also called the late product ; it gives the oriented volume of the parallelepiped spanned by the three vectors . ${\displaystyle {\vec {a}},{\vec {b}},{\vec {c}}}$

Applications

In geometry

Cosine theorem with vectors

The dot product makes it possible to simply prove complicated theorems that talk about angles.

Claim: ( cosine law )

${\displaystyle c^{2}=a^{2}+b^{2}-2\,a\,b\,\cos \gamma .}$

Proof: With the help of the drawn-in vectors it follows (The direction of is irrelevant.) Squaring the amount gives ${\displaystyle {\vec {c}}=-{\vec {b}}+{\vec {a}}.}$ ${\displaystyle {\vec {c}}}$

${\displaystyle |{\vec {c}}|^{2}={\vec {c}}\cdot {\vec {c}}=({\vec {a}}-{\vec {b}})\cdot ({\vec {a}}-{\vec {b}})={\vec {a}}\cdot {\vec {a}}-2\,{\vec {a}}\cdot {\vec {b}}+{\vec {b}}\cdot {\vec {b}}=|{\vec {a}}|^{2}+|{\vec {b}}|^{2}-2\,{\vec {a}}\cdot {\vec {b}}}$

and thus

${\displaystyle c^{2}=a^{2}+b^{2}-2\,a\,b\,\cos \gamma .}$

In physics

Example inclined plane

In physics , many quantities , such as work , are defined by scalar products: ${\displaystyle W}$

${\displaystyle W={\vec {F}}\cdot {\vec {s}}=|{\vec {F}}||{\vec {s}}|\cos \varphi =F_{s}\cdot s=F\cdot h}$

with the vector quantities force and path . It denotes the angle between the direction of the force and the direction of the path. With is the component of the force in the direction of the path, with the component of the path in the direction of the force. ${\displaystyle {\vec {F}}}$ ${\displaystyle {\vec {s}}}$ ${\displaystyle \varphi }$ ${\displaystyle F_{s}}$ ${\displaystyle h}$

Example: A wagon of the weight is transported over an inclined plane from to . The lifting work is calculated ${\displaystyle F}$ ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle W}$

${\displaystyle {\begin{aligned}W&={\vec {F}}\cdot {\vec {s}}=F\cdot h=F\cdot s\cdot \cos \varphi \\&=5\,\mathrm {N} \cdot 3\,\mathrm {m} \cdot \cos 63^{\circ }=6{,}81\,\mathrm {J} .\end{aligned}}}$

In general real and complex vector spaces

One takes the above properties as an opportunity to generalize the concept of the scalar product to any real and complex vector spaces . A scalar product is then a function that assigns a body element (scalar) to two vectors and fulfills the properties mentioned. In the complex case, the condition of symmetry and bilinearity is modified in order to save the positive definition (which is never fulfilled for complex symmetrical bilinear forms).

In general theory, the variables for vectors, i.e. elements of any vector space, are generally not indicated by arrows. The dot product is usually not denoted by a painting point, but by a pair of angle brackets. For the scalar product of the vectors and we write . Other common notations are (especially in quantum mechanics in the form of Bra-Ket notation), and . ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle \langle x,y\rangle }$ ${\displaystyle \langle x|y\rangle }$ ${\displaystyle (x,y)}$ ${\displaystyle (x|y)}$

Definition (axiomatic)

An inner product or inner product on a real vector space is a positively definite symmetric bilinear form, that is, for and the following conditions apply: ${\displaystyle V}$ ${\displaystyle \langle {\cdot },{\cdot }\rangle \colon V\times V\to \mathbb {R} ,}$ ${\displaystyle x,y,z\in V}$ ${\displaystyle \lambda \in \mathbb {R} }$

1. linear in each of the two arguments:
   • ${\displaystyle \langle x+y,z\rangle =\langle x,z\rangle +\langle y,z\rangle }$
   • ${\displaystyle \langle x,y+z\rangle =\langle x,y\rangle +\langle x,z\rangle }$
   • ${\displaystyle \langle \lambda x,y\rangle =\lambda \langle x,y\rangle }$
   • ${\displaystyle \langle x,\lambda y\rangle =\lambda \langle x,y\rangle }$
2. symmetrical: ${\displaystyle \langle x,y\rangle =\langle y,x\rangle }$
3. positive definite:
   • ${\displaystyle \langle x,x\rangle \geq 0}$
   • ${\displaystyle \langle x,x\rangle =0}$ exactly when ${\displaystyle x=0}$

A scalar product or inner product on a complex vector space is a positively definite Hermitian sesquilinear form that means for and the following conditions apply: ${\displaystyle V}$ ${\displaystyle \langle {\cdot },{\cdot }\rangle \colon V\times V\to \mathbb {C} ,}$ ${\displaystyle x,y,z\in V}$ ${\displaystyle \lambda \in \mathbb {C} }$

1. sesquilinear:
   • ${\displaystyle \langle x+y,z\rangle =\langle x,z\rangle +\langle y,z\rangle }$
   • ${\displaystyle \langle \lambda x,y\rangle ={\bar {\lambda }}\langle x,y\rangle }$    (semilinear in the first argument)
   • ${\displaystyle \langle x,y+z\rangle =\langle x,y\rangle +\langle x,z\rangle }$
   • ${\displaystyle \langle x,\lambda y\rangle =\lambda \langle x,y\rangle }$    (linear in the second argument)
2. hermitesch: ${\displaystyle \langle x,y\rangle ={\overline {\langle y,x\rangle }}}$
3. positive definite:
   • ${\displaystyle \langle x,x\rangle \geq 0}$(That is real follows from condition 2.) ${\displaystyle \langle x,x\rangle }$
   • ${\displaystyle \langle x,x\rangle =0}$ exactly when ${\displaystyle x=0}$

A real or complex vector space in which a scalar product is defined is called a scalar product space or Prähilbert space . A finite-dimensional real vector space with scalar product is also called Euclidean vector space , in the complex case one speaks of a unitary vector space. Correspondingly, the scalar product in a Euclidean vector space is sometimes referred to as the Euclidean scalar product, and that in a unitary vector space is referred to as the unitary scalar product . The term "Euclidean scalar product" but also specifically for the above described geometric scalar or described below standard scalar in use. ${\displaystyle \mathbb {R} ^{n}}$

Remarks

• Often every symmetrical bilinear form or every Hermitian sesquilinear form is referred to as a scalar product; with this usage the above definitions describe positively definite scalar products.
• The two axiom systems given are not minimal. In the real case, due to the symmetry, the linearity in the first argument follows from the linearity in the second argument (and vice versa). Similarly, in the complex case, due to the hermiticity, the semilinearity in the first argument follows from the linearity in the second argument (and vice versa).
• In the complex case, the scalar product is sometimes defined alternatively, namely as linear in the first and semilinear in the second argument. This version is preferred in mathematics and especially in analysis , while in physics the above version is predominantly used (see Bra and Ket vectors ). The difference between the two versions lies in the effects of the scalar multiplication in terms of homogeneity . After the alternative version applies to and and . The additivity is understood in the same way in both versions. The norms obtained from the scalar product according to both versions are also identical. ${\displaystyle x,y\in V}$ ${\displaystyle \lambda \in \mathbb {C} }$   ${\displaystyle \langle \lambda x,y\rangle =\lambda \langle x,y\rangle }$ ${\displaystyle \langle x,\lambda y\rangle ={\bar {\lambda }}\langle x,y\rangle }$
• A pre-Hilbert space, which completely with respect to the induced by the scalar standard is is referred to as the Hilbert space , respectively.
• The distinction between real and complex vector space when defining the scalar product is not absolutely necessary, since a Hermitian sesquilinear form corresponds in real to a symmetrical bilinear form.

Examples

Standard scalar product in R ⁿ and in C ⁿ

→ Main article : Standard scalar product

Based on the representation of the Euclidean scalar product in Cartesian coordinates, one defines the standard scalar product in the -dimensional coordinate space for through in linear algebra ${\displaystyle n}$ ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle x,y\in \mathbb {R} ^{n}}$

${\displaystyle \langle x,y\rangle =\sum _{i=1}^{n}x_{i}y_{i}=x_{1}{y_{1}}+x_{2}{y_{2}}+\dotsb +x_{n}{y_{n}}.}$

The “geometric” scalar product in Euclidean space treated above corresponds to the special case. In the case of the -dimensional complex vector space , the standard scalar product for is defined ${\displaystyle n=3.}$ ${\displaystyle n}$ ${\displaystyle \mathbb {C} ^{n}}$ ${\displaystyle x,y\in \mathbb {C} ^{n}}$

${\displaystyle \langle x,y\rangle =\sum _{i=1}^{n}{\bar {x}}_{i}y_{i}={\bar {x}}_{1}{y_{1}}+{\bar {x}}_{2}{y_{2}}+\dotsb +{\bar {x}}_{n}{y_{n}},}$

where the overline means the complex conjugation . In mathematics, the alternative version is also often used, in which the second argument is conjugated instead of the first.

The standard scalar product in or can also be written as a matrix product by interpreting the vector as a matrix ( column vector ): In the real case, the following applies ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle \mathbb {C} ^{n}}$ ${\displaystyle n\times 1}$

${\displaystyle \langle x,y\rangle =x^{T}y=y^{T}x,}$

where is the row vector which results from the column vector by transposing . In the complex case (for the left semilinear, right linear case) ${\displaystyle {x}^{T}}$ ${\displaystyle x}$

${\displaystyle \langle x,y\rangle =x^{H}y,}$

where is the row vector adjoint to Hermitian . ${\displaystyle x^{H}}$ ${\displaystyle x}$

General scalar products in R ⁿ and in C ⁿ

More generally, in the real case, every symmetric and positively definite matrix is ​​defined by ${\displaystyle A}$

${\displaystyle \langle x,y\rangle _{A}=x^{T}Ay=\langle x,Ay\rangle }$

a scalar product; likewise, in the complex case, for every positively definite Hermitian matrix, over ${\displaystyle A}$

${\displaystyle \langle x,y\rangle _{A}=x^{H}Ay=\langle x,Ay\rangle }$

defines a scalar product. Here, the angle brackets on the right-hand side denote the standard scalar product , the angle brackets with the index on the left-hand side denote the scalar product defined by the matrix . ${\displaystyle A}$ ${\displaystyle A}$

Every scalar product on or can be represented in this way by a positively definite symmetric matrix (or positively definite Hermitian matrix). ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle \mathbb {C} ^{n}}$

L ² scalar product for functions

→ Main article : L² scalar product

On the infinite-dimensional vector space of the continuous real-valued functions on the interval , the -scalar product is through ${\displaystyle C^{0}([a,b],\mathbb {R} )}$ ${\displaystyle [a,b]}$ ${\displaystyle L^{2}}$

${\displaystyle \langle f,g\rangle =\int _{a}^{b}f(x)g(x)\,\mathrm {d} x}$

defined for everyone . ${\displaystyle f,g\in C^{0}([a,b],\mathbb {R} )}$

For generalizations of this example see Prähilbertraum and Hilbertraum .

Frobenius scalar product for matrices

→ Main article : Frobenius scalar product

On the matrix space of the real - matrices is for by ${\displaystyle \mathbb {R} ^{m\times n}}$ ${\displaystyle (m\times n)}$ ${\displaystyle A,B\in \mathbb {R} ^{m\times n}}$

${\displaystyle \langle A,B\rangle =\operatorname {spur} \left(A^{T}B\right)=\sum _{i=1}^{m}\sum _{j=1}^{n}a_{ij}\,b_{ij}}$

defines a scalar product. Accordingly, in the space of complex matrices for by ${\displaystyle \mathbb {C} ^{m\times n}}$ ${\displaystyle (m\times n)}$ ${\displaystyle A,B\in \mathbb {C} ^{m\times n}}$

${\displaystyle \langle A,B\rangle =\operatorname {spur} \left(A^{H}B\right)=\sum _{i=1}^{m}\sum _{j=1}^{n}{\bar {a}}_{ij}\,b_{ij}}$

defines a scalar product. This scalar product is called the Frobenius scalar product and the associated norm is called the Frobenius norm .

Norm, angle and orthogonality

The length of a vector in Euclidean space corresponds in general scalar product spaces to the norm induced by the scalar product . This norm is defined by transferring the formula for the length from Euclidean space as the root of the scalar product of the vector with itself:

${\displaystyle \|x\|={\sqrt {\langle x,x\rangle }}}$

This is possible because due to the positive definiteness is not negative. The triangle inequality required as a norm axiom follows from the Cauchy-Schwarz inequality ${\displaystyle \langle x,x\rangle }$

${\displaystyle \left|\langle x,y\rangle \right|^{2}\leq \langle x,x\rangle \cdot \langle y,y\rangle .}$

If so, this inequality can ${\displaystyle x,y\neq 0,}$

${\displaystyle \left|{\frac {\langle x,y\rangle }{{\sqrt {\langle x,x\rangle }}\cdot {\sqrt {\langle y,y\rangle }}}}\right|\leq 1}$

be reshaped. Therefore, in general real vector spaces, one can also use

${\displaystyle \varphi =\arccos {\frac {\langle x,y\rangle }{{\sqrt {\langle x,x\rangle }}\cdot {\sqrt {\langle y,y\rangle }}}}}$

define the angle of two vectors. The angle defined in this way is between 0 ° and 180 °, i.e. between 0 and There are a number of different definitions for angles between complex vectors. ${\displaystyle \varphi }$ ${\displaystyle \pi .}$

In the general case, too, vectors whose scalar product is zero are called orthogonal:

${\displaystyle x\perp y\Longleftrightarrow \langle x,y\rangle =0}$

Matrix display

Is a n-dimensional vector space and a base of such, each dot on by a ( ) - matrix , the Gram matrix , are described in the scalar product. Your entries are the scalar products of the basis vectors: ${\displaystyle V}$ ${\displaystyle n}$ ${\displaystyle B=(b_{1},\dotsc ,b_{n})}$ ${\displaystyle V,}$ ${\displaystyle \langle {\cdot },{\cdot }\rangle }$ ${\displaystyle V}$ ${\displaystyle n\times n}$ ${\displaystyle G,}$

${\displaystyle G=(g_{ij})_{i,j=1,\dotsc ,n}}$   with     for ${\displaystyle g_{ij}=\langle b_{i},b_{j}\rangle }$ ${\displaystyle i,j=1,\dotsc ,n}$

The scalar product can then be represented with the help of the basis: Do the vectors have the representation with respect to the basis ${\displaystyle x,y\in V}$ ${\displaystyle B}$

${\displaystyle x=\sum _{i=1}^{n}x_{i}\,b_{i}}$   and   ${\displaystyle y=\sum _{j=1}^{n}y_{j}\,b_{j},}$

so in the real case

${\displaystyle \langle x,y\rangle =\left\langle \sum \limits _{i=1}^{n}x_{i}\,b_{i},\sum \limits _{j=1}^{n}y_{j}\,b_{j}\right\rangle =\sum \limits _{i=1}^{n}\sum \limits _{j=1}^{n}x_{i}\,y_{j}\,\langle b_{i},b_{j}\rangle =\sum \limits _{i,j=1}^{n}x_{i}\,y_{j}\,g_{ij}.}$

One denotes with the coordinate vectors ${\displaystyle x_{B},y_{B}\in \mathbb {R} ^{n}}$

${\displaystyle x_{B}={\begin{pmatrix}x_{1}\\\vdots \\x_{n}\end{pmatrix}}}$   and   ${\displaystyle y_{B}={\begin{pmatrix}y_{1}\\\vdots \\y_{n}\end{pmatrix}},}$

so it is true

${\displaystyle \langle x,y\rangle =\sum \limits _{i,j=1}^{n}x_{i}\,g_{ij}\,y_{j}={\begin{pmatrix}x_{1}&\dots &x_{n}\end{pmatrix}}\,{\begin{pmatrix}g_{11}&\dots &g_{1n}\\\vdots &\ddots &\vdots \\g_{n1}&\dots &g_{nn}\end{pmatrix}}\,{\begin{pmatrix}y_{1}\\\vdots \\y_{n}\end{pmatrix}}=x_{B}{}^{T}Gy_{B},}$

where the matrix product provides a matrix, i.e. a real number. With the will row vector designated by transposition from the column vector formed. ${\displaystyle (1\times 1)}$ ${\displaystyle x_{B}{}^{T}}$ ${\displaystyle x_{B}}$

In the complex case, the same applies

${\displaystyle \langle x,y\rangle =\sum \limits _{i,j=1}^{n}{\overline {x}}_{i}\,g_{ij}\,y_{j}={\begin{pmatrix}{\overline {x}}_{1}&\dots &{\overline {x}}_{n}\end{pmatrix}}\,{\begin{pmatrix}g_{11}&\dots &g_{1n}\\\vdots &\ddots &\vdots \\g_{n1}&\dots &g_{nn}\end{pmatrix}}\,{\begin{pmatrix}y_{1}\\\vdots \\y_{n}\end{pmatrix}}=x_{B}{}^{H}Gy_{B},}$

where the overline denotes complex conjugation and the line vector to be adjoint is. ${\displaystyle x_{B}{}^{H}}$ ${\displaystyle x_{B}}$

If there is an orthonormal basis , that is, holds for all and for all, then the identity matrix and it holds ${\displaystyle B}$ ${\displaystyle \langle b_{i},b_{i}\rangle =1}$ ${\displaystyle i}$ ${\displaystyle \langle b_{i},b_{j}\rangle =0}$ ${\displaystyle i\neq j,}$ ${\displaystyle G}$

${\displaystyle \langle x,y\rangle =\sum _{i=1}^{n}x_{i}\,y_{i}=x_{B}{}^{T}\,y_{B}}$

in the real case and

${\displaystyle \langle x,y\rangle =\sum _{i=1}^{n}{\overline {x}}_{i}\,y_{i}=x_{B}{}^{H}\,y_{B}}$

in the complex case. With regard to an orthonormal basis, the scalar product of and thus corresponds to the standard scalar product of the coordinate vectors and or ${\displaystyle x}$ ${\displaystyle y\in V}$ ${\displaystyle x_{B}}$ ${\displaystyle y_{B}\in \mathbb {R} ^{n}}$ ${\displaystyle \mathbb {C} ^{n}.}$

See also

• Quaternion
• Semi-inner product
• Dual pairing

literature

• Gerd Fischer : Linear Algebra. 15th edition. Vieweg Verlag, ISBN 3-528-03217-0 .
• Walter Rudin : Real and Complex Analysis . 2nd improved edition. Oldenbourg Wissenschaftsverlag, Munich 2009, ISBN 978-3-486-59186-6 .

Web links

Commons : dot product  - collection of images, videos and audio files

• Information and materials on the scalar product for the upper school level Landesbildungsserver Baden-Württemberg
• Joachim Mohr: Introduction to the scalar product
• Video: dot product . Jörn Loviscach 2010, made available by the Technical Information Library (TIB), doi : 10.5446 / 9742 .
• Video: dot product and vector product . Jörn Loviscach 2011, made available by the Technical Information Library (TIB), doi : 10.5446 / 9929 .
• Video: dot product, part 1 . Jörn Loviscach 2011, made available by the Technical Information Library (TIB), doi : 10.5446 / 10212 .
• Video: Dot product part 2, orthogonality . Jörn Loviscach 2011, made available by the Technical Information Library (TIB), doi : 10.5446 / 10213 .
• Video: Of vectors and their scalar product - vector calculation part 1 . Jakob Günter Lauth (SciFox) 2013, made available by the Technical Information Library (TIB), doi : 10.5446 / 17886 .

Individual evidence

1. ↑ Synonymous with: ${\displaystyle \cos(\varphi )={\frac {{\vec {a}}\cdot {\vec {b}}}{|{\vec {a}}||{\vec {b}}|}}}$
2. ^ Liesen, Mehrmann: Lineare Algebra . S. 168 .
3. ^ Walter Rudin : Real and Complex Analysis . 2nd improved edition. Oldenbourg Wissenschaftsverlag, Munich 2009, ISBN 978-3-486-59186-6 , p. 91 .
4. ^ Klaus Scharnhorst: Angles in complex vector spaces . In: Acta Applicandae Math. Volume 69 , 2001, p. 95-103 .