Pythagorean theorem
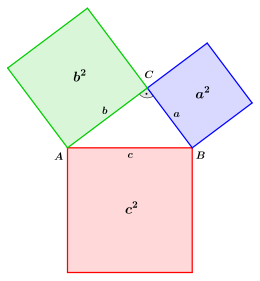
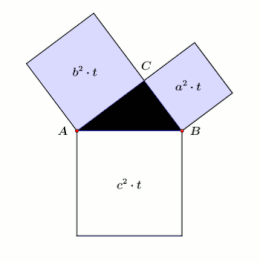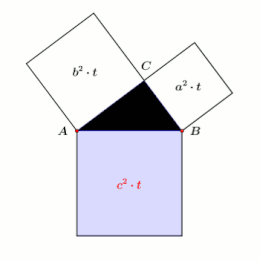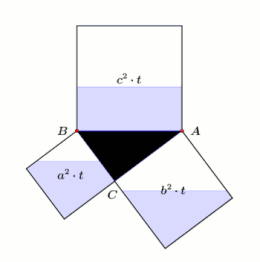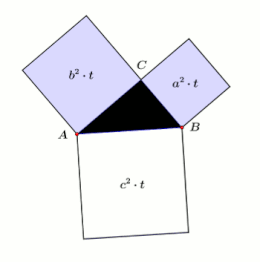
The Pythagorean theorem (also hypotenuse ) is one of the fundamental theorems of Euclidean geometry . It says that in all flat right triangles the sum of the areas of the cathetus squares is equal to the area of the hypotenuse square. If and are the lengths of the sides adjoining the right angle , the cathetus , and the length of the side opposite the right angle, the hypotenuse , then the theorem is expressed as an equation :
The theorem is named after Pythagoras of Samos , who is said to have been the first to find a mathematical proof for it, which is, however, controversial in research. The statement of the theorem was known in Babylon and India long before the time of Pythagoras , but there is no evidence that proof was also available there.
Mathematical statement
The Pythagorean theorem can be formulated as follows:
- If , and are the lengths of the sides of a right triangle, where and are the lengths of the cathetus and the length of the hypotenuse, then applies .
In a geometric interpretation, the sum of the areas of the two squares above the cathetus in a right-angled triangle is therefore equal to the area of the square above the hypotenuse.
The reverse of the sentence also applies:
- If the equation holds in a triangle with the side lengths , and , then this triangle is right-angled, with the right angle facing the side .
Closely related to the Pythagorean theorem are the law of heights and the law of legs . These two sentences and the Pythagorean theorem together form the Pythagorean sentence group . The cosine theorem described below is a generalization of the Pythagorean theorem.
use
Lengths in a right triangle
It follows directly from the Pythagorean theorem that the length of the hypotenuse is equal to the square root of the sum of the cathetus squares , i.e.
- .
A simple and important application of the theorem is to compute the third from two known sides of a right triangle. This is possible by transforming the equation for all sides:
The reverse of the theorem can be used to check that a given triangle is right angled. To this end, it is tested whether the equation of the theorem applies to the sides of the given triangle. Knowing the lengths of the sides of a given triangle is enough to determine whether it is right-angled or not:
- Are the side lengths z. B. , and , then results , and therefore the triangle is rectangular.
- Are the side lengths z. B. , and , then results , and therefore the triangle is not right angled.
From the Pythagorean theorem it follows that in a right triangle the hypotenuse is longer than each of the cathets and shorter than their sum. The latter also results from the triangle inequality .
Pythagorean triples
Of all the triples that satisfy the equation , there are an infinite number of which , and are each integers . These groups of three are called Pythagorean triples. The simplest of these triples consists of the numbers , and . Pythagorean triples have been used for the construction of right triangles since ancient times. An example is the twelve-knot cord used to lay a triangle whose sides have the lengths , and . The two short sides then form a right angle.
The great Fermatsche theorem states that the -th power of a number, if is, cannot be represented as the sum of two powers of the same degree. What is meant are whole basic numbers and natural exponents. Generally speaking, this means:
- The equation has no solution for integer and natural numbers .
This is amazing because there are an infinite number of solutions for. For these are the Pythagorean triplets.
Euclidean distance
The Pythagorean theorem provides a formula for the distance between two points in a Cartesian coordinate system . If two points and are given in a plane , then their distance is through
given. This makes use of the fact that the coordinate axes are perpendicular to one another. This formula can also be extended to more than two dimensions and then provides the Euclidean distance . For example, in three-dimensional Euclidean space
- .
proofs
Several hundred proofs are known for the theorem, making it the most proven mathematical theorem. As an example, in addition to the proof of volumes derived by addition, from the Zhoubi suanjing (arithmetic classic of the Zhou gnomon), another four geometric proofs are presented below. A fifth proof from 1875 by James A. Garfield can be found under Garfield's proof of Pythagorean theorem , which is very similar to the proof by supplementation.
Geometric proof by supplement
Four congruent right-angled triangles with the sides , and (hypotenuse) are inserted into a square with the side length . This can be done in two ways as shown in the diagram.
The areas of the left and right squares are the same (side length ). The left one consists of the four right-angled triangles and one square with side length , the right one with the same triangles and one square with side length and one with side length . The area corresponds to the sum of the area and the area , that is
- .
An algebraic solution results from the left picture of the diagram. The large square has the side length and thus the area . If you subtract the four triangles from this area, each of which has an area of (i.e. in total ), the area remains. So it is
- .
Dissolving the bracket supplies
- .
If you now subtract on both sides , the Pythagorean theorem remains.
Shear proof
One possibility is to shear the cathetus squares into the hypotenuse square. In geometry, the shear of a rectangle is understood as the transformation of the rectangle into a parallelogram while maintaining the height. During the shear, the resulting parallelogram has the same area as the starting rectangle. The two smaller squares can then be converted into two rectangles, which together fit exactly into the large square.
In the case of an exact proof, it must then be proven via the congruence theorems in the triangle that the smaller side of the resulting rectangles corresponds to the relevant hypotenuse section. As usual in the animation, the height is indicated with and the hypotenuse segments with .
Proof with similarities
It is not absolutely necessary to use (explicitly) surfaces to prove the Pythagorean theorem. It is geometrically more elegant to use similarities. As soon as you have convinced yourself by calculating the angle sums in the triangle that the two angles in the picture below must be the same, you can see that the triangles , and are similar. The proof of the Pythagoras theorem then results as shown in the picture, one also proves the cathetus theorem and the addition of both variants of the catheter theorem results in the theorem of Pythagoras itself. This derivation can be illustrated with the similarity of the squares and the similarity of their adjacent triangles to explain. Since their area is proportional to the area of the adjacent squares, the equation represents
the sentence.
Proof of the reversal
The inversion of the theorem can be proven in various ways, but a particularly simple proof is obtained if one uses the Pythagorean theorem itself to prove its inversion.
A second triangle is constructed for any triangle whose sides meet the condition . This has a right angle, the leg lengths of which correspond to the side lengths of and . According to the Pythagorean Theorem, the length of the hypotenuse in this second triangle is now the length of the side of the starting triangle . Thus the two triangles have the same side lengths and are congruent due to the first congruence theorem (SSS). This means that their angles are then also the same, that is, the starting triangle also has a right angle that is opposite the side .
Generalizations and Delimitation
Cosine law
The cosine law is a generalization of the Pythagorean theorem for arbitrary triangles:
- ,
where the angle between the sides is and . The cosine law therefore differs from the Pythagorean theorem by the term . Since the cosine of zero is, this term drops at a right angle away, and there is a special case of the Pythagorean theorem. Conversely, if the relationship is valid in a triangle
- ,
so must be, from which it follows, and hence the triangle is right-angled. The same applies to acute triangles
and for obtuse triangles
- .
Generalization of Thabit ibn Qurra
A generalization going back to Thabit ibn Qurra provides for the squares over two sides of any triangle a rectangle over the third side, the area of which corresponds to the sum of the two square areas.
For any triangle with sides , angles at and height , you construct an isosceles triangle whose base is on the side and which has the height. In addition, its two base angles are the same size as when it is an acute angle. On the other hand, if an obtuse angle is used, the base angles should be. Furthermore, the corner point of the isosceles triangle, which is on the same side of as, is designated with E and the other corner point on the same side as with . However, this applies only in the case , for instead swapped to and . In the case , the isosceles triangle coincides with the height and the points and accordingly with the point . If one defines and , then the following applies:
For applies here and the above equation delivers the Pythagorean theorem.
Analogous to the Pythagorean Theorem, the statement can be proven directly using similar triangles, where the triangles , and are similar.
Owing to
Qurra's generalization also provides a geometrical representation of the correction term in the law of cosines as a rectangle added to or subtracted from the square above the side to give an area equal to the sum of the areas of the squares above the sides and .
Face set by pappus
Another generalization to arbitrary triangles is provided by the area formula of Pappus . Here, from any two parallelograms over two sides of any triangle, a clearly defined parallelogram over the third side of the triangle results, the area of which corresponds to the sum of the areas of the two starting parallelograms. If the two starting parallelograms are squares, then in the case of a right triangle you get a square over the third side and thus the Pythagorean theorem.
The parallelogram over the third side is obtained by extending the two sides of the starting parallelograms, which are parallel to the sides of the triangle, and connecting their point of intersection with the corner point of the triangle, which is also on both parallelograms. This connecting line provides the second pair of sides of the parallelogram over the third side (see drawing).
Similar figures erected over the sides of the right triangle
A generalization of the Pythagorean theorem with the help of three similar figures above the triangle sides (in addition to the already known squares ) was already introduced by Hippocrates of Chios in the 5th century BC. Is known and, probably two hundred years later, Euclid added elements to his work :
"In the right-angled triangle, the straight figure above the hypotenuse is the same as the similar and similarly constructed figures above the cathetus."
If one erects a figure similar to the other two over each of the three sides and the original triangle (Fig. 1) with the surfaces and then because of their similarity:
If you put and in the form
we get for the sum:
According to the Pythagorean theorem , for is substituted and thus results:
While Euclid's proof is only valid for convex polygons (polygons), the theorem is also valid for concave polygons and even for similar figures with curved boundaries, these figures also arising from a respective side of the original triangle. The areas and the circles shown in Figure 2 are created from the sides and the pentagons .
To make it clear that circles or semicircles alone, i.e. H. without polygons over the sides, can be used for generalization, the Pythagorean theorem is expanded with the number of circles
From the set with squares
becomes, with the corresponding side lengths and as radii, a generalization with circles
or a generalization with semicircles:
The basic idea behind this generalization is that the area of a planar figure is proportional to the square of each linear dimension, and in particular proportional to the square of the length of each side.
Scalar product spaces
If one abstracts from ordinary Euclidean space to general scalar product spaces , i.e. vector spaces with a scalar product , then the following applies:
If two vectors and are orthogonal to each other, i.e. their scalar product , then the following applies due to the linearity of the scalar product
- ,
where denotes the norm induced by the scalar product .
If one relates this sentence again to Euclidean space, then and stand for the cathetus and a right triangle. stands for the length of the hypotenuse .
This generalization of the Pythagorean theorem can also be found in abstract mathematical structures, such as infinite-dimensional function spaces. The reverse is also true. If the equation applies, the two vectors are orthogonal to one another. The proposition can be generalized even further. If an orthogonal system consists of pairwise orthogonal vectors , then by repeated application of the above argument it follows:
The corresponding statement even applies to infinite sums if one considers a sequence of vectors which are all orthogonal to one another. If the series now converges , then it also converges and the following applies:
The proof of the second claim follows from the continuity of the scalar product. Another generalization leads to Parseval's equation .
Further generalizations
The thigh transversal theorem , the Stewart theorem , the Ptolemy theorem and the theorem of the British flag can also be considered generalizations of the Pythagorean theorem . The latter represents a generalization both in plane and in space. The Pythagorean equation is also contained in the Apollonios equation .
A spatial analogue is de Gua's theorem . Here the right-angled triangle is replaced by a right-angled tetrahedron and the side lengths are replaced by the areas of the side surfaces. Both the Pythagorean Theorem and the De Gua Theorem are special cases of a general theorem on n-simplexes with a right-angled corner .
Differences in non-Euclidean geometry
Non-Euclidean geometries are geometries in which the axiom of parallels does not apply. An example of this is the geometry of the spherical surface . There the Pythagorean theorem no longer applies, because the internal angle theorem does not apply in such geometries , i.e. the sum of the angles of a triangle differs from 180 °. Another example is the “ curved ” space of Albert Einstein's general theory of relativity .
history
Babylon and India
Already on a Babylonian cuneiform tablet , which is dated to the time of the Hammurabi dynasty (approx. 1829 to approx. 1530 BC), there is a geometric problem with a solution, in which the theorem for calculating lengths (in the sexagesimal system ) has been used:
A bar, 0; 30 (= 30/60 GAR = 1/2 GAR ≈ 3 m long)
From above it came down 0; 6 (= 6/60 GAR).
What has he removed from below?
0; 30 (= 30/60) square, 0; 15 (= 900/3600 = 15/60) you see.
0; 6 (= 6/60) subtracted from 0; 30 (= 30/60), 0; 24 (= 24/60) you see.
0; 24 (= 24/60) square, 0; 9.36 (= 576/3600) you see.
0; 9.36 (= 576/3600) of 0; 15 (= 900/3600) subtract, 0; 5.24 (= 324/3600) you see.
0; 5.24 (= 324/3600) has what as a square root? 0; 18 (= 18/60).
0; 18 (= 18/60 GAR) on the ground he has moved away.
This results in:
- so and on .
However, the sources do not show any interest on the part of the Babylonians in a mathematical proof .
The cuneiform tablet Plimpton 322 also contains various Pythagorean triples, among others
- , as well as ,
which suggests a method for calculating such triples.
In Indian Sulbasutras (“rules of shearing” or “guides to the art of measuring”), which dates from around the 6th to the 4th century BC. A few Pythagorean triples can be found. In addition, the theorem was already generally pronounced and used there. How it was justified is not certain.
China
The phrase was known as the phrase of the Gougu (勾股定理) in ancient China . In the script Zhoubi suanjing (“Arithmetic Classic of the Zhou Gnomonic”), which dates from around the 1st century BC. BC to the 6th century AD, the so-called "hypotenuse figure" (Xian-tu) illustrates a proof of the theorem given there using the example of the right-angled triangle (gougu) with pages 3, 4 and 5 . It is also used in Jiu Zhang Suanshu ("Nine Books of Arithmetic Technique", 1st century AD), the classic mathematical work of China with a collection of 263 problems, their solutions and the possible solutions. Liu Hui (3rd century AD) probably gave in his commentary on the “Nine Books” in the ninth chapter a proof of decomposition.
The controversial role of Pythagoras

The name of the sentence after the Greek philosopher Pythagoras (6th century BC) is only attested in late sources. Therefore, the question of the role of Pythagoras is highly controversial in research. Various hypotheses can be considered:
- Pythagoras took over the theorem from the Babylonians, his role was only that of a mediator of oriental knowledge to the Greeks. According to ancient sources, he went on a trip to Egypt, he is said to have even been to Babylonia, but the credibility of the reports about his travels is disputed.
- Pythagoras discovered the theorem independently of oriental mathematics and proved it for the first time. This view was widespread in ancient times.
- Pythagoras owed his knowledge of the matter to oriental sources, but was the first to find evidence of it. In fact, the Babylonians and Egyptians seem to have only been interested in the application of the theorem for practical purposes, not in any generalized proof. For example, the oldest known arithmetic book in the world, the Egyptian arithmetic book of Ahmes (also Papyrus Rhind ) from the 17th century BC contains BC, already complicated tasks, but there is no generalization, it is not defined and proven.
- Pythagoras played no part in the history of the proposition; only later Pythagoreans may have found the first proof.
The historians of science Walter Burkert and Leonid Zhmud represent opposing positions . At best, Burkert considers Pythagoras' mediator role; Zhmud attributes mathematical achievements to him such as the proof of the theorem and emphasizes his independence from oriental mathematics.
Euclid , who in the second half of the 4th century BC BC, in his famous work, collected elements of the mathematical knowledge of his time, offered a proof, but did not connect the theorem with Pythagoras. The oldest evidence that the theorem was associated with Pythagoras is an epigram of an Apollodorus, who can possibly be identified with the philosopher Apollodorus of Cyzicus; in this case the verses are from the second half of the 4th century BC. The text reads:
When Pythagoras once found the famous drawing, he
brought glorious bulls to God as a sacrifice.
Apollodorus does not state which "famous" drawing or figure he meant, but later authors, including Diogenes Laertios , who quoted the two verses in the 3rd century, assumed that it was the "Pythagorean theorem". This tradition, according to which Pythagoras offered a cattle sacrifice to a god in gratitude for giving him the knowledge, contradicts the fact, passed down by numerous ancient sources, that Pythagoras and the Pythagoreans rejected animal sacrifices in principle.
Literary reception
Hans Christian Andersen wrote a proof of the Pythagorean theorem in poetry in 1831 with the title Formens evige Magie (Et poetisk Spilfægterie).
illustration
Objects that describe the Pythagorean theorem with the help of liquids are very common. The animated principle sketch opposite is, so to speak, the front view of a rotatable exhibit at the Phaeno Science Center in Wolfsburg. On the sides of the central right triangle, flat transparent containers with the depth are attached. Their square base areas are equal to the areas of the cathetus squares or the hypotenuse square. The containers are therefore marked with , and . Is the exhibit in its initial position ( bottom), the flows in and blue filled to the brim water over the corners of the triangle and from entirely and thus completely filled . It follows
- ,
divided by gives it
Related topics
- Pythagorean addition - the square root of the sum of the squares of several values
- Trigonometric Pythagoras - the transfer of the theorem to the trigonometric functions sine and cosine
- Little moon of Hippocrates
literature
- Anna M. Fraedrich: The sentence group of Pythagoras. Spektrum Akademischer Verlag, Heidelberg 1994, ISBN 3-86025-669-6 .
- Hans Schupp: Elementary Geometry. UTB, Stuttgart 1977, ISBN 3-506-99189-2 , pp. 114-118.
- Alexander K. Dewdney : Journey into the Inside of Mathematics. Birkhäuser, Berlin 2000, ISBN 3-7643-6189-1 , pp. 47-76.
- Eli Maor : The Pythagorean Theorem: A 4,000-year History. Princeton University Press, Princeton 2007, ISBN 0-691-12526-0 .
- Alfred S. Posamentier: The Pythagorean Theorem: The Story of Its Power and Beauty. Prometheus Books, Amherst 2010, ISBN 978-1-61614-181-3 .
Web links
- Numerous animated proofs of the Pythagorean Theorem , State Education Server Baden-Württemberg
- Evidence for the Pythagorean Theorem. ( Memento from September 12, 2010 in the Internet Archive ). Chair of Mathematics Didactics, University of Erlangen-Nuremberg
- Geometric Evidence for the Pythagorean Theorem (Video)
- Collection of 122 proofs of the Pythagorean theorem on cut-the-knot (English)
- Interactive tutorial with evidence, assignments and lots of links
- Eric W. Weisstein : Pythagorean theorem . In: MathWorld (English). (Also contains various pieces of evidence)
Individual evidence
- ↑ Eli Maor : The Pythagorean Theorem: A 4,000-year History. Princeton University Press, Princeton 2007, ISBN 0-691-12526-0 ., P. XIII (foreword).
- ^ Zhou bi, Mathematical Canon of the Zhou Gnomonic. Bielefeld University, accessed on May 24, 2019 .
- ↑ Michael de Villiers: Thabit's Generalization of the Theorem of Pythagoras . In: Learning and Teaching Mathematics. No. 23, 2017, pp. 22-23.
- ↑ Aydin Sayili: Thâbit Ibn Qurra's Generalization of the Pythagorean Theorem. In: Isis. Volume 51, No. 1, 1960, pp. 35-37 ( JSTOR ).
- ↑ George Gheverghese Joseph: The Crest of the Peacock: Non-European Roots of Mathematics. Princeton University Press, 2011, ISBN 9780691135267 , p. 492.
- ^ Howard Eves: Pappus's Extension of the Pythagorean Theorem. In: The Mathematics Teacher. Volume 51, No. 7 (November 1958), pp. 544-546 ( JSTOR 27955752 ).
- ^ Claudi Alsina, Roger B. Nelsen: Charming Proofs: A Journey Into Elegant Mathematics. MAA, Washington DC 2010, ISBN 978-0-88385-348-1 , pp. 77-78 ( limited preview in Google Book Search).
- ^ A b Thomas Heath: A History of Greek Mathematics, Volume 1 ,. (a) Hippocrates' quadrature of lunes. In: wilbourhall. Clarendon Press, Oxford, 1921, pp. 183 ff., Illustration p. 185 , accessed September 25, 2019 .
- ^ Oskar Becker : The mathematical thinking of antiquity, volume 3. Mathematics of the 5th century. In: Google Books. Vandenhoeck & Ruprecht, Göttingen, 1966, p. 58 , accessed on September 26, 2019 .
- ↑ a b Euclid: Stoicheia. Book VI. (PDF; 529 kB) In: opera-platonis.de/euklid. Retrieved May 19, 2019 .
- ↑ Naber: The Pythagorean Theorem, a Theorem about Squares? Bielefeld University, accessed on May 24, 2019 .
- ↑ London, British Museum , cuneiform tablet 85196 .
- ↑ Helmuth Gericke : Mathematics in antiquity and the Orient. Berlin 1984, p. 33 f.
- ↑ Kurt Vogel : Pre-Greek Mathematics. Part II: The Mathematics of the Babylonians. Hanover / Paderborn 1959, p. 67 f.
-
↑ Kurt Vogel : Pre-Greek Mathematics. Part II: The Mathematics of the Babylonians. Hanover / Paderborn 1959, p. 20.
Franz Lemmermeyer : The mathematics of the Babylonians. (PDF; 7.6 MB) 2.4 The Babylonian system of measurement. University of Heidelberg, October 27, 2015, p. 44 ff. , Accessed on May 23, 2019 . - ↑ Helmuth Gericke: Mathematics in antiquity and the Orient. Berlin u. a. 1984, pp. 66-69.
- ^ Oskar Becker: The mathematical thinking of antiquity. Göttingen 1966, p. 55 f. ( limited preview in Google Book search).
- ↑ Detailed explanation of the facts in Thomas L. Heath: The thirteen books of Euclid's Elements. Volume 1. 2nd edition, New York 1956, pp. 360-364.
- ↑ Oskar Becker: The basics of mathematics in historical development. Freiburg 1964, p. 20.
- ^ Jean-Claude Martzloff: A History of Chinese Mathematics. Berlin u. a. 1997, pp. 124, 126.
- ↑ Helmuth Gericke: Mathematics in antiquity and the Orient. Berlin 1984, p. 178 f.
- ^ Jean-Claude Martzloff: A History of Chinese Mathematics. Berlin u. a. 1997, p. 298 f.
-
^ Oskar Becker: The mathematical thinking of antiquity. Göttingen 1966, p. 56 ( limited preview in the Google book search).
Helmuth Gericke: Mathematics in Antiquity and the Orient. Berlin 1984, p. 179, on the other hand, sees no evidence in this. - ^ Jean-Claude Martzloff: A History of Chinese Mathematics. Berlin u. a. 1997, pp. 296-298. The associated drawing, which is required for a correct understanding, has not been preserved.
- ^ Walter Burkert: Wisdom and Science. Studies on Pythagoras, Philolaus and Plato. Nuremberg 1962, p. 405 f. , 441 ff.
- ^ Leonid Zhmud: Science, philosophy and religion in early Pythagoreanism. Berlin 1997, pp. 141–151, 160–163 ( limited preview in Google book search).
- ↑ See also Thomas L. Heath: The thirteen books of Euclid's Elements. Volume 1. 2nd edition. New York 1956, pp. 350-360.
- ^ Euclid: Elements. The stoicheia. Book 1, sentence 47 (PDF; 5.6 MB) In: opera-platonis.de. Retrieved July 15, 2019 .
- ↑ Apollodoros after Diogenes Laertios 8:12, translated by Otto Apelt : Diogenes Laertios: Life and opinions of famous philosophers. 3. Edition. Hamburg 1990, p. 116.
- ^ Leonid Zhmud: Pythagoras and the Early Pythagoreans. Oxford 2012, pp. 59, 257, 267-269.
- ^ Walter Burkert: Wisdom and Science. Studies on Pythagoras, Philolaus and Plato. Nuremberg 1962, p. 168 and note 152, p. 405 f.
- ^ Hans Christian Andersen: HC Andersens samlede værker. Volume 7: Digte I. 1823-1839. Copenhagen 2005, pp. 311-313, commentary pp. 638-639 ( visithcandersen.dk ).
- ↑ Hans-Joachim Schlichting : The world seen physically. - Forms of Eternal Magic. In: hjschlichting.wordpress.com. March 9, 2017, accessed July 13, 2020 .
- ↑ Hans-Joachim Schlichting: The world seen physically. The Pythagorean Theorem - revisited. In: hjschlichting.wordpress.com. March 5, 2017. Retrieved July 11, 2019 .