circle
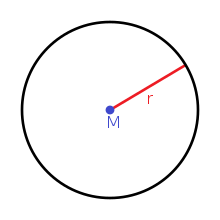
A circle is a flat geometric figure . It is defined as the set of all points on a plane that are at a constant distance from a given point on this plane (the center point ). The distance between the points on the circle to the center of the radius or radius of the circle, it is a positive real number . The circle is one of the classic and fundamental objects of Euclidean geometry .
Even the ancient Egyptians and Babylonians tried to approximate the area of the circle. The circle was of particular interest in ancient Greece because of its perfection. For example, Archimedes tried unsuccessfully to use the compass and ruler tools to convert the circle into a square with the same area in order to be able to determine the area of the circle. Such a method for calculating the area is called the quadrature of the circle . It was not until 1882 that Ferdinand von Lindemann was able to demonstrate by demonstrating a special property of the circle number that this task could not be solved .
Explanations of words
Circular areas
According to the definition mentioned at the beginning, a circle is a curve , i.e. a one-dimensional structure, and not a two-dimensional surface . Since the word “circle” is often used imprecisely for the enclosed area, the terms circle line, circle edge or circle periphery are often used instead of circle - in contrast to the circular area or circular disk. Mathematicians then differentiate between the closed circular surface or disc and the open one (or the inside of a circle ), depending on whether the circular line belongs to it or not.
Bow, tendon, sector, segment and ring
A connected subset of the circle (i.e. the circular line) is an arc . A line connecting two points on the circular line is called a circular chord . Each chord has two arcs. The longest tendons of the circle are those that go through the center point, i.e. the diameters . The associated arcs are called semicircles. If the chord is not a diameter, the arcs are of different lengths.
A sector of a circle (section of a circle) is an area bounded by two radii and an arc between them. If the two radii form a diameter, the sector is also referred to as a semicircle.
Circle segments (circle segments ) are enclosed by an arc and a chord.
A circular ring is created when a smaller circle with the same center is cut out of a circle.
Tangent, passerby and secant
There are three possibilities for the position of a straight line in relation to a given circle:
- If the distance between the center and the straight line is smaller than the radius of the circle, the circle and straight line have two (different) points of intersection and the straight line is called secant (Latin secare = to cut). Sometimes the special case of a secant that runs through the center of a circle is referred to as the center.
- If the distance between the center point and the straight line corresponds to the radius, there is exactly one common point. It is said that the straight line touches the circle, and the straight line is called a tangent (Latin tangere = to touch). A tangent is perpendicular ( orthogonal , normal) to the corresponding radius at the point of contact .
- If the distance between the center of the circle and the straight line is greater than the radius of the circle, then the circle and the straight line have no point in common. In this case, the straight line is called a passer-by . This name has no direct Latin origin, but was probably derived from French. or Italian passante = formed by people passing by. The Latin root is passus = step.
Formal definition
In a plane , a circle with a center and a radius is the set of points
The radius is a positive real number and denotes the length of the route .
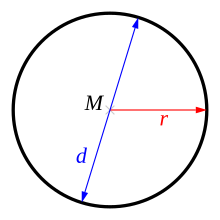
The double radius is called diameter and is often referred to as. Radius and diameter are linked through the relationships or with each other.
Sometimes every line that connects the center point with a point on the circular line is called a radius , and every line that goes through the center point and whose two end points lie on the circle line is called a diameter. In this way of speaking, the number is the length of each radius and the number is the length of each diameter.
The open circular area is formally defined as the set of points
the closed circular disk as
history
Time of the Egyptians and Babylonians

Along with the point and the straight line , the circle is one of the oldest elements of pre-Greek geometry. Four thousand years ago, the Egyptians studied it in their geometry studies. They were able to approximate the area of a circle by subtracting one ninth of its length from the diameter d and multiplying the result by itself. So you did the math
and thus approximately (with a deviation of only about +0.6%) the area of a circular area. This approximation was found in the ancient Egyptian treatise Papyrus Rhind , it can be obtained if the circle is approximated by an irregular octagon.
The Babylonians (1900 to 1600 BC) used a completely different method to calculate the area of the circular disk. In contrast to the Egyptians, they started from the circumference , which they estimated to be three times the diameter of the circle . The area was then estimated to be one twelfth of the square of the circumference, that is
with a deviation of −4.5% a significantly worse result.
The Babylonians also dealt with segments of a circle. They could calculate the length of the chord or the height of the segment of a circle (the line perpendicular to the center of the chord between the chord and the circumference). With this they established the chord geometry , which was later developed by Hipparchus and which Claudius Ptolemaios placed at the beginning of his astronomical textbook Almagest .
Antiquity
The Greeks are mostly seen as the founders of the science of nature. Thales of Miletus (624-546 BC) is considered to be the first major philosopher of this time who dealt with mathematics . He brought knowledge of geometry from Egypt to Greece, such as the statement that the diameter bisects the circle. Other statements about geometry were made by Thales himself. The sentence , named after Thales today , says that peripheral angles in a semicircle are right angles . In particular, Thales was the first to use the concept of the angle .
The first known definition of the circle goes back to the Greek philosopher Plato (428 / 427-348 / 347 BC), which he formulated in his dialogue Parmenides :
"That is probably round, the outermost parts of which are everywhere the same distance from the center."
The Greek mathematician Euclid of Alexandria lived about 300 years before Christ . Little is known about himself, but his work in geometry has been considerable. His name is still in use today in contexts such as Euclidean space , Euclidean geometry or Euclidean metrics . His most important work was The Elements , a thirteen-volume treatise in which he summarized and systematized the arithmetic and geometry of his time. He deduced the mathematical statements from postulates and thus founded Euclidean geometry. The third volume of the elements dealt with the doctrine of the circle.
By Archimedes , who probably lived between 287 BC. BC and 212 BC BC lived in Sicily, a detailed treatise with the title Circular Measurement has come down to us. In this work he proved that the area of a circle is equal to the area of a right triangle with the circle radius as the one and the circumference as the other leg . The area of the circle can be given as ½ · radius · circumference . With this knowledge he traced the problem of squaring the circle back to the question of whether the circumference could be constructed from the given radius.
In his paper circle measurement Archimedes could also show that the circumference of a circle greater than 3 10 / 71 and less than 3 1 / 7 of the diameter. For practical purposes, this approximation is 22 / 7 (~ 3.143) still used today.
From these two statements it concludes that the area of a circle almost as to the square of its diameter 11 / 14 behaves. Euclid already knew that the area of a circle is proportional to the square of its diameter. Archimedes gives a good approximation of the constant of proportionality here.
In another work on spirals , Archimedes describes the construction of the Archimedean spiral that was later named after him . With this construction it was possible for Archimedes to plot the circumference of a circle on a straight line. In this way the area of a circle could now be determined exactly. However, this spiral cannot be constructed with a compass and ruler.
Apollonios von Perge lived about 200 years before Christ. In his conic section theory Konika , among other things, he understood the ellipse and the circle as the intersection of a straight circular cone - just as it is still defined today in algebraic geometry . His findings go back to his predecessors Euclid and Aristaios (around 330 BC), whose written treatises on conic sections, however, have not survived.
The Apollonian problem is also named after Apollonios of constructing the circles that touch the given circles with the Euclidean tools ruler and compass. However, in comparison to Euclid's elements, which also formed the basis of geometry in the Middle Ages, the works of Apollonios initially only found attention in the Islamic area. In Western Europe, his books only became more important in the 17th century, when Johannes Kepler recognized the ellipse as the true orbit of a planet around the sun.
Renaissance
In the history of science, the period between AD 1400 and AD 1630 is usually called the Renaissance , even if the period does not correspond to the periodization of art history, for example. During this time Euclid's elements received more attention again. They were among the first books to be printed and were published in many different editions in the centuries that followed. Erhard Ratdolt produced the first printed edition of the elements in Venice in 1482 . One of the most important editions of Euclid's Elements was published by the Jesuit Christoph Clavius . He added a sixteenth book and other extensive additions to the actual texts of Euclid, in addition to the books XIV and XV of late antiquity. For example, he added a construction of the common tangents of two circles.
19th century
After preliminary work by Leonhard Euler , who established Euler's identity , Johann Heinrich Lambert and Charles Hermite , Ferdinand von Lindemann was able to prove in 1882 that the number is transcendent . That is, there is no polynomial function with rational coefficients for which π is a zero. However, since it was shown as early as the 17th century that the circle number had to be a zero of such a polynomial function in order for the quadrature of the circle to work with compass and ruler, it was also proven that there can be no such procedure.
Equations
In analytical geometry , geometric objects are described with the help of equations . Points in the plane are usually represented by their Cartesian coordinates and a circle is then the set of all points whose coordinates satisfy the respective equation.
Coordinate equation
The Euclidean distance of a point from the point is calculated as
The coordinate equation is obtained by squaring the defining equation
for the points on the circle with center point and radius . When multiplied it results:
With
- , and .
An important special case is the coordinate equation of the unit circle
Function equation
Since the circle is not a function graph , it cannot be represented by a function equation. As a makeshift, a pair of functional equations
be used. For the unit circle this is simplified to
Parametric representation
Another way of describing a circle using coordinates is to use the parameter display (see also polar coordinates ):
Here the coordinates and are expressed by the parameter that can assume all values .
If one also applies these equations specifically to the unit circle, one obtains:
It is also possible to display parameters without resorting to a trigonometric function (rational parameterization), but the entire set of real numbers is required as a parameter range and the point is only reached as a limit value for .
The following then results for the unit circle:
Complex representation
In the complex number plane , the circle around with radius can be described by the equation
represent. The parameter representation is obtained with the help of the complex exponential function
Three-point form of a circular equation
The coordinate equation of the circle using three given points that do not lie on a straight line is obtained by transforming the 3-point form (removal of the denominator and quadratic addition):
Circle through three points
From the three-point form and coordinate equation results for the circle through three given points with
and the determinants
for the center point and the radius
If the three given points lie on a straight line, then .
Circle calculation
Circle number
Since all circles are similar , the ratio of circumference and diameter is constant for all circles. The numerical value of this ratio is used in elementary geometry as a definition for the number of circles . This is a transcendent number that has also been shown to be of outstanding importance in many areas of higher mathematics.
scope
In the context of elementary geometry, the ratio of the circumference to its diameter is for any circle. Thus applies
With is meant the radius of the circle.
Circular area
The area of the circular area ( lat. Area: area) is proportional to the square of the radius or the diameter of the circle. It is also known as the content of a circle.
In order to obtain the formula for the circle content, limit value considerations are essential. This can be seen quite clearly from the adjacent drawing:
The area of the circle has the same decomposition as the area of the figure on the right. As the sector division becomes finer, this approximates a rectangle with length and width . The area formula is thus
The area formula can be proven, for example, by integrating the circular equation or using the approximation described below using regular polygons.
diameter
The diameter of a circle with area and with radius can be passed through
to calculate.
curvature
A less elementary property of the circle compared to the quantities described so far is its curvature . For a precise definition of the curvature, terms from analysis are required, but it can be easily calculated due to the symmetry properties of the circle. The curvature at each point clearly indicates how much the circle deviates from a straight line in the immediate vicinity of the point . The curvature of the circle at the point lets through
Calculate, again being the radius of the circle. Unlike other mathematical curves , the circle has the same curvature at every point. Apart from the circle, only the straight line has a constant curvature, with . For all other curves, the curvature depends on the point .
More formulas
In the following formulas, denotes the sector angle in radians . If the angle denotes in degrees , the conversion applies .
| Formulas for the circle | |
|---|---|
| Area of a circular ring | |
| Length of an arc | |
| Area circular sector | |
| Area of a segment of a circle | |
| Length of the circular tendon | |
| Height (circle segment) | |
Approximations for the area
Since the circle number is a transcendent number , there is no construction method with compasses and ruler with which one can determine the area exactly. In addition, transcendent numbers are also irrational , and therefore have no finite expansion of decimal fractions , which is why the area of the circle with a rational radius also has no finite expansion of decimal fractions. For these reasons, different approximation methods for the area and thus also the circumference of a circle have been developed to this day. Some of the approximation methods, such as the method explained in the section Approximation using polygons , can provide a result that is as precise as desired by repeating them multiple times.
Approximation by squares
A circle with a radius is circumscribed with a square the length of the side . A square with the diagonal is also inscribed on it. The area of the outer square is that of the inner according to the triangular area formula and the mean value is thus . With this approximation the circular area is determined with a relative error of less than 5%.
Counting in a grid
The circular area can be approximated by placing many small squares under it (e.g. with graph paper ). If you count all the squares that lie completely within the circle, you get a value that is slightly too low for the area, if you also count all the squares that merely intersect the circle, the value is too large. The mean value of both results gives an approximation for the area of the circle, the quality of which increases with the fineness of the square grid.
Approach through integration
The area of the circle can be composed of strips that are very narrow in relation to the radius . The equations are used for this
- and .
Approximation by polygons
Another way of determining the area of a circle is to draw a regular hexagon in the circle , the corners of which lie on the circle. If the middle of the sides is projected from the center onto the circle and these new points are connected with the old corners, a regular dodecagon is created . If this process is repeated, a 24-sided, a 48-sided and so on are created.
In each hexagon, the sides are the same length as the perimeter radius. The sides of the following polygons result from the sides of the previous one with the help of Pythagoras' theorem . The areas of the polygons can be determined exactly from the sides by calculating the triangle areas . They are all slightly smaller than the circular area, which they approach as the number of corners increases.
The same can be done with a hexagon that is drawn on the outside of the circle, with the center of its sides lying on it. A decreasing sequence of area dimensions is obtained, the limit value of which is again the circular area.
Geometric sentences and terms around the circle
Symmetry and imaging properties
The circle is a geometrical figure of very high symmetry . Every straight line through its center is an axis of symmetry . In addition, the circle is rotationally symmetrical , i.e. i.e., every rotation around the center point maps the circle onto itself. In group theory , the mentioned symmetry properties of the circle are characterized by its symmetry group . Formal arises for the orthogonal group that is the group of the orthogonal - matrices .
All circles with the same radius are congruent to one another , so they can be mapped to one another through parallel shifts. Any two circles are similar to each other . They can always be mapped to one another by means of a centric extension and a parallel shift.
Circle angles and angle sets

A chord with endpoints A and B divides a given circle into two arcs. An angle with vertex C on one of the circular arcs is called a circumferential angle or peripheral angle . The angle with the vertex at the center M is called the center angle or central angle.
In the special case that the chord contains the center point, i.e. is a diameter of the circle, the center point angle is a straight angle of 180 °. In this situation, a fundamental statement of circular geometry applies, Thales's theorem: It says that circumferential angles over a diameter are always right angles, i.e. 90 °. The circle around the right triangle is also called the Thales circle in this situation .
Even in the case of any given chord, all circumferential angles that lie on the same circular arc are of the same size. This statement is also called the set of circumferential angles . The circular arc on which the apex of the circumferential angles lie is called the barrel arc. If the circumferential angle and central angle are on the same side of the chord, then the central angle is twice as large as the circumferential angle (circular angle set). Two circumferential angles, which are on opposite sides of the tendon, add 180 ° to each other.
The circumferential angle is the same size as the acute tendons tangent angle between the chord and the plane passing through one of its endpoints tangent (tangent angle tendons set).
Sentences about tendons, secants and tangents
For circles the true sinews set two tendons [AC] and [BD] each cutting in a point S, then: which states
d. that is, the products of the respective tendon sections are the same.
Two chords of a circle that do not intersect each other can be extended to secants that are either parallel or intersect at a point S outside the circle. If the latter is the case, the secant sentence applies analogously to the chord sentence
In the case of a secant that intersects the circle at points A and C, and a tangent that touches the circle at point B, the secant-tangent principle applies : If S is the intersection of secant and tangent, then it follows
Circles and incircles
If A, B, C are three points that do not lie on a straight line, i.e. form a non-degenerate triangle , then there is a clearly defined circle through these points, namely the circumference of triangle ABC. The center of the circumference is the intersection of the three perpendiculars of the triangle. Likewise, each triangle can be inscribed with a clearly defined circle that touches the three sides, i.e. That is, the sides of the triangle form tangents to the circle. This circle is called the inscribed circle of the triangle. Its center point is the intersection of the three bisectors .
In elementary geometry further be circles at the triangle considered: The excircles lie outside the triangle and touch one side and the extensions of the other two sides. Another interesting circle on the triangle is the Feuerbachkreis , named after Karl Wilhelm Feuerbach . The three side centers and the three base points of the heights lie on it . Since the three midpoints of the lines between the vertical intersection and the corners of the triangle lie on it, the Feuerbach circle is also called the nine-point circle . Its center, like the center of gravity , the center of the circumference and the intersection of the height, lies on Euler's straight line .
In contrast to triangles, irregular polygons (polygons) with more than three corners generally have no perimeter or inscribed circle. For regular polygons both exist, drawn in or not, but always. A square having a perimeter is inscribed quadrilateral mentioned. A convex quadrilateral is a chordal quadrilateral if and only if opposite angles add up to 180 °. A square that has an inscribed circle is called a tangent square . A convex quadrilateral is a tangent quadrilateral if the sum of the side lengths of two opposite sides is equal to the sum of the other two side lengths.
Circular reflections and furniture transformations
The mirroring of a circle, also called inversion, is a special representation of planar geometry that describes a “mirroring” of the Euclidean plane on a given circle with a center point and radius . If a given point, then its image point is determined by the fact that it lies on the half-line and its distance from the equation
Fulfills. The mirroring of the circle maps the inside of the given circle onto its outside and vice versa. All circle points of are mapped onto themselves. Circular reflections are true to angle , orientation reversal and true to circle . The latter means that generalized circles - that is, circles and straight lines - are mapped back to generalized circles.
The execution of two circular reflections one behind the other results in a furniture transformation. Möbius transformations - another important class of images of the plane - are therefore also true to angle and true to the circle, but preserve orientation.
Circular reflections and Möbius transformations can be displayed particularly clearly with the help of complex numbers: In the case of a circular reflection of a point on the circle , the formula for the image point is
The following applies to the reflection on the unit circle .
Furniture transformations of the complex plane are made by broken linear functions of the shape
shown with and .
Constructions with compasses and ruler
A classic problem of geometry is the construction of geometric objects with compasses and ruler in a finite number of construction steps from a given set of points. In each step, straight lines can be drawn through given or already constructed points and circles can be drawn around such points with a given or already constructed radius. The points thus constructed result from the intersection of two straight lines, two circles or a straight line with a circle. Naturally, circles play an important role in all constructions with compasses and rulers.
In the following some constructions that are important in connection with the geometry of circles will be addressed as examples.
Thales district

For the construction of the Thaleskreis over a given route , the center of this route is first constructed, which is also the center of the Thaleskreis. For this purpose , two short circular arcs with the same radius are struck around and around , whereby the choice must be large enough that the four circular arcs intersect at two points and . This is e.g. B. for the case. The line then cuts in the center . The Thales circle you are looking for is now the circle with the center and radius .
Construction of tangents
Given a point outside of a circle with a center point and the two tangents to the circle that run through the point are to be constructed. This elementary construction task can be easily solved with the help of Thales' theorem: Construct the Thales circle with the line as a diameter. The points of intersection of this circle with are then the points of contact of the tangents sought.
Area doubling
The area of a circle can be doubled geometrically by drawing a square, one corner of which is in the center of the circle, with two further corners on the arc. A circle is drawn through the fourth corner around the old center. This procedure was presented in the 13th century in the building works book of Villard de Honnecourt . This method works because (according to the Pythagorean Theorem )
and thus the area of the large circle
is exactly twice as large as that of the small circle.
Division of circles
Another construction problem that was already investigated in ancient times is the division of circles. Here, for a given natural number, a regular corner should be inscribed in a given circle . The corner points located on the circle then divide it into circular arcs of equal length. This construction is not possible for everyone : With the help of the algebraic theory of field extensions it can be shown that it is feasible if and only if a prime factorization of the form
has with and pairwise distinct Fermat primes , so primes of the form . So that the construction is possible for example , but not for z. B. . Carl Friedrich Gauß proved in 1796 that the construction of the regular seventeenth- corner is possible using only compasses and rulers .
Circle calculation in analysis
In modern analysis , the trigonometric functions and the circle number are usually initially defined without recourse to the elementary geometric view and to special properties of the circle. For example, sine and cosine can be defined as a power series through their representation . A common definition for the value of is then twice the smallest positive zero of the cosine.
The circle as a curve
In differential geometry , a branch of analysis that studies geometric shapes with the help of differential and integral calculus , circles are viewed as special curves . These curves can be described as a path with the aid of the parameter representation mentioned above . If the origin of coordinates is placed in the center of a circle with a radius , then the function with
given such a parameterization. With the help of the trigonometric formula, it follows for the Euclidean norm of the parameterized points , that is, they actually lie on a circle with a radius . Since the sine and cosine - periodic are functions that define the interval corresponds to from exactly a circle circulation.
Circumference
The circumference of the circle results from the length of the way through integration to
The same applies to the length of the arc given by . This gives the parameterization of the circle according to the arc length
with .
Area
The area of the circular disk , i.e. the measure of the quantity , can be used as a (two-dimensional) integral
being represented. To avoid the somewhat tedious calculation of this integral in Cartesian coordinates, it is favorable to a transformation , to polar coordinates to perform. This results in
Another possibility for calculating the area of a circle is to apply Leibniz's sector formula to the parametric representation of the edge of the circle. With , you also get with it
curvature
For the parameterization of the circle derived above according to its arc length results
The curve of the circle is therefore obtained
So the curvature of the circle is constant and the radius of curvature is just its radius.
In differential geometry it is shown that a flat curve is uniquely determined by its curvature, except for congruence. The only flat curves with constant positive curvature are therefore circular arcs. In the borderline case that the curvature is constantly equal to 0, straight lines result.
Isoperimetric problem
Of all surfaces of the Euclidean plane with a given circumference, the circular surface has the largest surface area. Conversely, the circular area has the smallest circumference for a given area. In the plane, the circle is therefore the uniquely determined solution of the so-called isoperimetric problem. Although this vividly plausible fact was already known to mathematicians in ancient Greece, formal proofs were not provided until the 19th century. Since a curve is sought that maximizes a functional , namely the enclosed area, from a modern point of view this is a problem of the calculus of variations . A common proof of piecewise continuous curves uses the theory of Fourier series .
Generalizations and Related Topics
sphere
It is possible to generalize the circle as an object of the plane in three-dimensional space. Then you get the envelope of a sphere . In mathematics, this object is called the sphere or, more precisely, the 2-sphere. Analogously, the 2-sphere can be generalized to dimensions to -sphere . In this context, the circle is also called 1-sphere.
Conic sections

In plane geometry , the circle can be understood as a special ellipse in which the two focal points coincide with the center of the circle. Both semi-axes are equal to the circle radius. The circle is therefore a special conic section: It is created as the section of a straight circular cone with a plane perpendicular to the cone axis. It is therefore a special case of a two-dimensional quadric .
This results in a further, equivalent definition for circles ( circle of Apollonios ): A circle is the set of all points in the plane for which the quotient of their distances from two given points is constant. The two points lie on an outgoing ray at a distance or alternately on the polar of the other point as a pole. Similar definitions exist for the ellipse (constant sum), hyperbola (constant difference) and the Cassinian curve (constant product of the distances).
Circles in synthetic geometry
In synthetic geometry , circles in certain affine planes (for example pre-Euclidean planes ) can be defined without a concept of distance solely by an orthogonality relation , by using the theorem of the circumference (central perpendicular theorem ) to define the circle. As a result, a weaker concept of “distance” or “equal length” of pairs of points can be introduced in such planes. → See also Pre-Euclidean level .
Drawing in the digital grid
Several algorithms have been developed for drawing approximated circles in a grid of points , see grid of circles . These techniques are particularly important for computer graphics . The basic arithmetic operations are sufficient for the two-color rasterization of circles .
See also
- Semicircle
- Unit circle
- Circular arc
- District sector
- Circle segment
- Circular ring
- Circle angle
- Tendon (geometry)
- Great circle
- Small circle
- District group
- District loyalty
- Zindler curve
- Malfatti circle
literature
- Ilka Agricola , Thomas Friedrich : Elementary Geometry. 3. Edition. Vieweg + Teubner, Wiesbaden 2011, ISBN 978-3-8348-1385-5 .
- Christian Bär : Elementary Differential Geometry. 2nd Edition. Walter de Gruyter, Berlin 2010, ISBN 978-3-11-022458-0 .
- Hartmut Wellstein, Peter Kirsche: Elementary Geometry. A task-oriented introduction. Vieweg + Teubner, Wiesbaden 2009, ISBN 978-3-8348-0856-1 .
Web links
- Circle. In: "Mathematical Handicrafts"
- Eric W. Weisstein : Circle . In: MathWorld (English).
Individual evidence
- ↑ Ilja Nikolajewitsch Bronštein: Pocket book of mathematics. Verlag Harri Deutsch, 5th edition, Thun and Frankfurt 2001, p. 143.
- ↑ Max Koecher, Aloys Krieg: level geometry. 3. Edition. Springer, Berlin / Heidelberg / New York 2007, ISBN 978-3-540-49327-3 , p. 143.
- ^ Scriba, Schreiber: 5000 years of geometry. 2005, pp. 32-33.
- ↑ Christoph J. Scriba, Peter Schreiber: 5000 years of geometry: history, cultures, people (from counting stone to computer). Springer, Berlin / Heidelberg / New York, ISBN 3-540-67924-3 , p. 13.
- ↑ Christoph J. Scriba, Peter Schreiber: 5000 years of geometry: history, cultures, people (from counting stone to computer). Springer, Berlin / Heidelberg / New York, ISBN 3-540-67924-3 , p. 18.
- ↑ Christoph J. Scriba, Peter Schreiber: 5000 years of geometry: history, cultures, people (from counting stone to computer). Springer, Berlin / Heidelberg / New York, ISBN 3-540-67924-3 , pp. 19-20.
- ↑ Christoph J. Scriba, Peter Schreiber: 5000 years of geometry: history, cultures, people (from counting stone to computer). Springer, Berlin / Heidelberg / New York, ISBN 3-540-67924-3 , pp. 31-33.
- ↑ Max Koecher, Aloys Krieg: level geometry . 3rd revised and expanded edition. Springer, Berlin / Heidelberg 2007, corrected reprint 2009, ISBN 978-3-540-49327-3 , p. 145.
- ↑ Christoph J. Scriba, Peter Schreiber: 5000 years of geometry: history, cultures, people (from counting stone to computer). Springer, Berlin / Heidelberg / New York, ISBN 3-540-67924-3 , pp. 49-50.
- ↑ a b In English translation by Thomas Little Heath : The works of Archimedes, ed. In modern notation, with introductory chapters. University press, Cambridge 1897. Circular measurement: p. 91 ff., About spirals: p. 151 ff., (Digitized version).
- ↑ Euclid's elements . XII, § 2.
- ↑ See Gericke: Antike und Orient. P. 120 ff.
- ^ Scriba, Schreiber: 5000 years of geometry. 2005, pp. 40-42.
- ↑ Christoph J. Scriba, Peter Schreiber: 5000 years of geometry: history, cultures, people (from counting stone to computer). Springer, Berlin / Heidelberg / New York, ISBN 3-540-67924-3 , pp. 72-73.
- ↑ Christoph J. Scriba, Peter Schreiber: 5000 years of geometry: history, cultures, people (from counting stone to computer). Springer, Berlin / Heidelberg / New York, ISBN 3-540-67924-3 , pp. 247-248.
- ↑ Christoph J. Scriba, Peter Schreiber: 5000 years of geometry: history, cultures, people (from counting stone to computer). Springer, Berlin / Heidelberg / New York, ISBN 3-540-67924-3 , pp. 405-406.
-
↑ Hurwitz: Quelques applications geometriques des series de Fourier. Annales de l'Ecole Normale, Volume 19, 1902, pp. 357-408.
The proof can be found, for example, in Blaschke: Lectures on differential geometry. Volume 1, Springer, 1924, p. 45.












![[\ mathrm {MX}]](https://wikimedia.org/api/rest_v1/media/math/render/svg/df392cf388e4c6cf3cd7223cc72665a3b88d1baa)


























































































































![f \ colon [0, 2 \ pi] \ to \ R ^ 2](https://wikimedia.org/api/rest_v1/media/math/render/svg/63a694de043d7335d09672ba01fab40576d7b778)




![[0.2 \ pi]](https://wikimedia.org/api/rest_v1/media/math/render/svg/348d40bf3f8b7e1c00c4346440d7e2e4f0cc9b91)



![f | _ {[0, t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aa7502f93282d8ef8893d1b846ff3cd7d4bf183f)


![s \ in [0.2 \ pi r]](https://wikimedia.org/api/rest_v1/media/math/render/svg/35189ce5963764c3dc16536a2e25bae90c49361d)
















