Amount (math)
A set is a compound, a combination of individual elements . The set is one of the most important and fundamental concepts in mathematics , and set theory is concerned with looking at it .
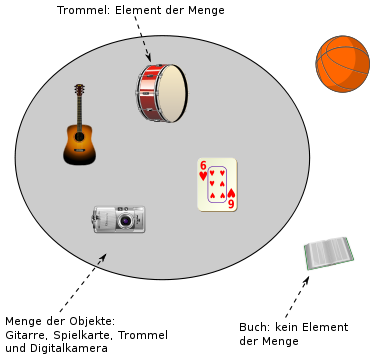
When describing a set, it is all about the question of which elements it contains. This means that for every object it must be clear whether it belongs to the set or not. It is not asked whether an element is contained more than once or whether there is a sequence among the elements. A set does not have to contain an element - there is exactly one set without elements, the “ empty set ”. In mathematics, the elements of a set are often numbers, points of a space or, in turn, sets. However, the concept is applicable to any object: e.g. B. in statistics on random samples, in medicine on patient files, on a market stall on a bag of fruit.
If the order of the elements is important, then one speaks of a finite or infinite sequence if the elements of the sequence can be enumerated with the natural numbers (the first, the second, etc.). Finite sequences are also called tuples . Elements can occur more than once in a tuple or a sequence. A structure that contains like a lot of elements, whereby the number of copies of each element is also important, but not the order, is called a multiset .
Concept and notation of quantities
The term quantity goes back to Bernard Bolzano and Georg Cantor . In Bolzano's manuscripts from the years between 1830 and 1848 it says: “Epitomes, in which the way in which their parts are connected with one another should not be taken into account, in which everything we distinguish in them is determined as soon as only its parts are determined, it is precisely for the sake of this quality that it deserves to be designated by a name of its own. In the absence of another suitable word, I allow myself to use the word amount for this purpose ". Cantor described a lot "naively" (but also see Cantor's axioms of sets ) as a "summary of certain, well-differentiated objects of our perception or our thinking into a whole". The objects of the set are called elements of the set. Neither the term “set” nor the term “element” is defined in a mathematical sense; nor are they defined as or in axioms . Modern set theory and thus a large part of mathematics is based on the Zermelo-Fraenkel axioms (or: ZFA), Neumann-Bernays-Gödel axioms or other axiom systems. We have a natural, intuitively correct understanding of sets; however, the term “the set of all sets that do not contain themselves as an element” leads to a contradiction, Russell's antinomy ; as well as “the set of all sets”.
An illustration of the concept of quantity, which is attributed to Richard Dedekind , is the picture of a sack that contains certain things (which can be individually defined). This idea is useful, for example, for the empty set: an empty sack. The empty set is therefore not “nothing”, but the content of a container that does not contain any of the things intended for it as content. The “container” itself only refers to the specific sort and type of elements to be summarized. But this notion has its limits. A container remains the same even if you change its content. This is different with sets: they change their identity when you add new elements or remove existing ones. In this respect, it is better to think of the quantity as “the contents of a container”.
Finite sets can be specified (especially if they have relatively few elements) by enumerating their elements (enumerating set notation), for example . That is, it applies, for example .
Often it is practically or in principle (with infinite sets) impossible to enumerate the elements of a set. But there is another notation in which the elements of a set are determined by a property, for example . (Say: "M is the set of all x for which: 'x is a basic color'.")
In addition, Dedekind coined the synonym of the system into which he combined elements. This designation is still partly used today, so a “set of vectors ” is also called a vector system for short .
Other spellings
Other notations for quantities can be seen as abbreviations for the dimensional notation:
- The enumerated notation can be understood as an abbreviation for the cumbersome notation .
- To spell with ellipsis only some elements are listed as examples, such as: . It can only be used if the law of education is clear from these examples or from the context. What is obviously meant here is the amount that can be written intensional as . This notation is often used for infinite quantities. This describes the set of even natural numbers that are greater than 2.
- New sets can also be formed using set operations , such as from and the intersection . This can be written intensional as .
- There is also the inductive definition of sets in which at least one basic element is specified explicitly and then at least one rule as to how another element can be derived from an element. So the above set can also be described by
- i) is in and
- ii) for each in is also in and
- iii) only elements obtained by i) and (no, single or repeated) application of ii) are in .
Mightiness
For finite sets the cardinality (or cardinality ) is equal to the number of elements in the set; that is a natural number including zero. The term can also be generalized to infinite sets; it turns out that two infinite sets need not be of equal power. The power of a crowd is generally noted with , occasionally also with .
Basic relationships between sets
The things that are in a crowd are called elements. If an object element of a set , we formally wrote this: . Negation ( no element of ) one writes as: . Historically, the element sign goes back to the Greek letter ε as the first letter of εστί ( estí , it is ) and was used for the first time in 1889 by Giuseppe Peano .
Equality of quantities and extensionality
equality
Two sets are called the same if they contain the same elements.
This definition describes the extensionality and thus the fundamental property of sets. Formally:
In fact, a lot has to be described intensively . This means: A statement form is specified (with an object variable that should have a well-defined set of definitions ), so that if and when applies. For this one then writes:
For every quantity there are many different forms of statement that describe it. The question of whether two given forms of proposition and describe the same set is by no means trivial. On the contrary: Many mathematical questions can be formulated in this form: "Are and the same amount?"
Many proofs of equality use equivalence .
Extensionality
If two sets contain the same elements, they are the same. The way in which the membership of the elements in the sets is described is irrelevant. The characteristic of sets that the type of description does not matter is called their extensionality (from the Latin extensio = extension; relates to the scope of the content).
However, infinite sets usually have to be described "intensional" (descriptive set notation) (from Latin intensio = tension; relates to the characteristics of the content). That means: A set is described by a certain condition or property that all elements of the set (and only these) fulfill: for example , read “be the set of all for which applies: is an even natural number and greater than 2” or shorter: “be the set of all even natural numbers ”.
It is sometimes difficult to decide whether two intensionally described sets are the same. To do this, it must be determined whether the properties from the intensional descriptions are logically equivalent (if one property is true, so is the other, and vice versa).
Empty set
The set that does not contain an element is called the empty set. It is also referred to as or and has the power . From the extensionality it follows immediately that there is only one empty set: Every “other” empty set that contains the same (ie no) elements would be the same. Hence, and are different, since the latter set contains a different set as an element.
Nonempty set
A non-empty set is a set that is not the empty set . A non-empty set therefore contains at least one element . The thickness of a non-empty set is greater than 0.
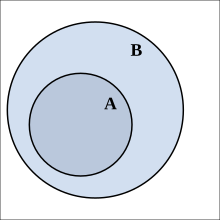
Subset
A set is called a subset of a set if every element of is also an element of .
is then called a superset (seldom: superset) of . Formally:
- .
Thus in particular is also a lot of A subset of himself . The empty set is a subset of any set.
is a true subset of (or is a true superset of ) if is a subset of , but is different from, i.e. every element of is also an element of , but (at least) one element exists in that is not contained in.
The relation “is a subset of” forms a partial order . The relation “real subset” is a strict partial order.
There are two notations in use for subsets:
- for “subset” and for “real subset” or
- for “subset” and for “real subset”.
The first-mentioned system corresponds to that introduced by Bertrand Russell (cf. Principia Mathematica ) and clarifies the analogy to the signs and . It will be used in this article, but both systems are widely used.
The negation of the relations , and can be denoted by the crossed out respective relation symbol, for example by . It is also possible to swap the order of the two arguments if the relation symbol is also reversed. So instead of also , instead of also and instead of also can be written. It is also conceivable that these relation symbols can be crossed out and turned over at the same time.
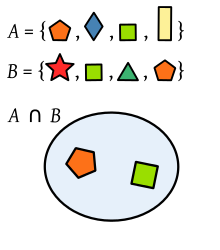
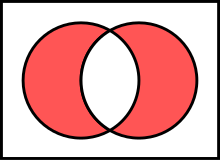
Intersection (cut, also "average")
A non-empty set of sets is given. The intersection (also average ) of is the set of elements contained in each element set of . Formally:
- .
The intersection of is also characterized by the fact that for every set :
- .
Sets of elements without common elements are called non-element or disjoint . Their intersection is the empty set.
Is a pair set , so one writes for
and reads this: intersected with (or: the intersection of and ) is the amount of all elements contained in as well as in .
This notation can easily be generalized to the average of a finite number of sets .
Different notation for the average of any number of quantities:
The elements of the set , which are themselves sets, are denoted by. An “ index set ” ( lambda ) is introduced so that is. The intersection is then written as:
- ,
thus the set of all elements that are contained in all sets .
An older term for the average is internal product or product of the first kind. This is then also called
- or
written. In particular, the last notation is reserved by many authors for the Cartesian product (see below) and should therefore not be used for the intersection in order to avoid misunderstandings.
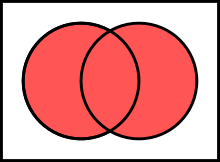
Union (union set)
This is the dual term for the intersection : The union of is the set of elements that are contained in at least one element set of . Formally:
- .
The union of is also characterized by the fact that for every set it holds:
- .
In contrast to is also explained when it is empty, and that results .
For one writes (analogous to the average):
and reads this: united with (or: the union of and ) is the set of all elements contained in or in . The “or” is to be understood here non-exclusively: The union also includes the elements that are contained in both sets.
If sets contain no common elements, i.e. they are disjoint , the symbol is also used for the union of these disjoint sets. However, while the sign of the union intuitively with the Junktors ( or ) can be identified, must be between the sign of the disjoint union and the connective ( exclusionary or are) distinguished.
Using a suitable index set , we write:
- .
This notation is also suitable for the union of finitely many sets .
As an older term for this, the sum is sometimes used and then written
- or .
Caution: The term sum is also used today for the disjoint union of sets.
Difference and complement
The difference is usually only defined for two sets: The difference set (also remainder ) of and (in this order) is the set of elements that are contained in but not in . Formally:
The difference set is also characterized by the fact that for every set :
- .
In contrast to intersection and union, the difference is neither commutative nor associative .
Is , the difference is also called the complement of in . This term is mainly used when there is a basic set that includes all the sets in question in a particular study. This amount does not have to be mentioned in the following, and
is simply called the complement of . Other spellings for are , or .
Symmetrical difference
The amount
is called the symmetrical difference of and . It is the set of all elements that are in one set, but not both. When using the exclusive or ("either-or": or ) you can also use
write.
Cartesian product
The product set or the Cartesian product is another way of linking sets. The elements of the Cartesian product of two sets are, however, not elements of the initial sets, but more complex objects. Formally, the product set of and is defined as
and thus the set of all ordered pairs whose first element is off and whose second element is off. Using n-tuples , the Cartesian product can also be generalized for the connection of finitely many sets :
- ,
If the quantities are all equal to a quantity , the product quantity is also written as short . A general function term is required for the product set of a family of sets with an arbitrary index set . It is the set of all functions that an element of the set assigns to each index element , i.e.
Whether such a Cartesian product is not empty, that is, whether there are always such functions as indicated on the right-hand side of this definition equation, is closely related to the axiom of choice .
If the quantities are all equal to a quantity , the product quantity is also written as .
Power set
The power set of is the set of all subsets of .
The power set of always contains the empty set and the set . Thus , is a one-element set. The power set of a one-element set is , therefore, contains two elements. In general, if it has exactly elements, then has the number of elements , that is . This also motivates the spelling instead .
In the case of infinite sets, the term is not unproblematic: There is demonstrably no method that could list all subsets. (See: Cantor's second diagonal argument .) In the case of an axiomatic structure of set theory ( e.g. ZFC ), the existence of the power set must be demanded by its own power set axiom .
Constructive mathematicians therefore regard the power set of an infinite set as a fundamentally open area to which - depending on the progress of mathematical research - new sets can always be added.
Examples of set operations
We consider the sets , and . For example:
- ,
- , ,
- Respect for the complements applies , , , .
- , , ,
- , ,
- = 3, = = 2, = 0, = 1
- , , ,
- , ,
- ,
Specific examples are named here again.
- The amount of all two-digit “ schnapps numbers ” is . 33 is an element of this set, 23 is not.
- The set of natural numbers is a proper subset of the set of whole numbers .
Further terms
- Subsets of the real straight line, the plane or the Euclidean space or even subsets in any topological space are often also called point sets . In the latter case, the term point set topology is still used today in the English-speaking world .
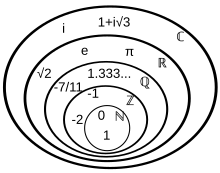
- In modern mathematics, the number ranges are built up step by step using the methods of set theory (with the empty set as the only basic building block), from the prime numbers and natural numbers to the whole numbers and rational numbers to the real numbers and on to the complex numbers and even beyond that.
- At school, set theory has at times achieved great importance under the heading of new mathematics .
- In the case of infinite quantities , special phenomena occur with regard to the usual order relations .
- Set diagrams are used to illustrate the relationships between quantities .
- Relationships between the elements of one set and those of another are described by "assignments" ( relations ), clear assignments by "images" ( functions ).
See also
literature
- Klaus Kursawe: Quantities, Numbers, Operations . Scripta Mathematica. Aulis Verlag Deubner, Cologne 1973, ISBN 3-7614-0176-0 .
- Hans-Dieter Gerster: propositional logic, sets, relations . Studying and teaching mathematics. Franzbecker, Hildesheim 1998, ISBN 3-88120-287-0 .
- Adolf Fraenkel : Introduction to set theory . Springer, Berlin / Heidelberg / New York 1928. (Reprint: Dr. Martin Sendet, Walluf 1972, ISBN 3-500-24960-4 )
- Erich Kamke: set theory . 6th edition. Walter de Gruyter, Berlin 1969.
- Paul R. Halmos: Naive set theory . Vandenhoeck & Ruprecht, Göttingen 1968, ISBN 3-525-40527-8 .
- H. Schinköthe: Quantities and lengths, textbook on the elementary foundations of mathematical thinking and its development for the areas of: kindergarten, preschool, elementary school, special school, mathematical therapy . RESI, Volxheim 2000 (Libri / BoD), ISBN 3-8311-0701-7 .
- Oliver Deiser: Introduction to set theory . Georg Cantor's set theory and its axiomatization by Ernst Zermelo . 3. Edition. Springer Verlag , Berlin / Heidelberg 2010, ISBN 978-3-642-01444-4 , doi : 10.1007 / 978-3-642-01445-1 .
Web links
- Literature on quantities in the catalog of the German National Library
Individual evidence
- ↑ Bernard Bolzano : Introduction to the theory of size and first terms of the general theory of size . Ed .: Jan Berg (= Eduard Winter et al. [Ed.]: Bernard-Bolzano-Gesamtausgabe . II, A). tape 7 . Friedrich Frommann Verlag, Stuttgart / Bad Cannstatt 1975, ISBN 3-7728-0466-7 , p. 152 .
- ↑ See text passage with the set definition by Georg Cantor.png for the corresponding passage in the article Contributions to the foundation of transfinite set theory - Mathematische Annalen (journal volume 46) ( Memento from April 23, 2014 in the Internet Archive ).
- ↑ ti.inf.uni-due.de (PDF) Retrieved on November 18, 2011.
- ^ As explained in Bertrand Russell , Alfred North Whitehead : Principia Mathematica . 1st edition. Cambridge University Press, Cambridge, S. 26 (English, University of Michigan [PDF; accessed October 23, 2011] 1910–1913). and earlier at Peano .
- ↑ For emptiness a logical problem arises with this formulation (even more clearly with ) according to the rule “ ex falso quodlibet ”: Which one should be meant? In analogy to for all others, non-empty ones are mostly used because of .
- ↑ If you consider yourself an index set and set for , then this notation corresponds to the definition above .
- ^ John B. Conway : A Course in Point Set Topology . Springer Science + Business Media, Cham 2014, ISBN 978-3-319-02367-0 , doi : 10.1007 / 978-3-319-02368-7 .
- ^ Wolfgang Rautenberg : measuring and counting . Heldermann Verlag, Lemgo 2007, ISBN 978-3-88538-118-1 .