Cartesian product

The Cartesian product of the two sets and ${\displaystyle A\times B}$ ${\displaystyle A=\{x,y,z\}}$ ${\displaystyle B=\{1,2,3\}}$

The Cartesian product or quantity of product is in the set theory a basic structure from given amounts to generate a new set. The ambiguous term “ cross product ” is occasionally used for the Cartesian product . The Cartesian product of two sets is the set of all ordered pairs of elements of the two sets, where the first component is an element of the first set and the second component is an element of the second set. More generally, the Cartesian product of several sets consists of the set of all tuples of elements of the sets, the sequence of the sets and thus of the corresponding elements being fixed. The result set of the Cartesian product is also product quantity , Cross quantity or amount of compound called. The Cartesian product is named after the French mathematician René Descartes , who used it to describe the Cartesian coordinate system and thus established analytic geometry .

Product of two sets

definition

The Cartesian product (read "A cross B") of two sets and is defined as the set of all ordered pairs , where one element is out and one element is out. Each element is made with each item of combined. Formally, the Cartesian product is through ${\displaystyle A\times B}$ ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle (a,b)}$ ${\displaystyle a}$ ${\displaystyle A}$ ${\displaystyle b}$ ${\displaystyle B}$ ${\displaystyle A}$ ${\displaystyle B}$

${\displaystyle A\times B:=\left\{(a,b)\mid a\in A,b\in B\right\}}$

Are defined. In particular, it is also possible to form the Cartesian product of a set with itself and then write

${\displaystyle A^{2}=A\times A=\left\{(a,a')\mid a,a'\in A\right\}}$.

Occasionally the term “cross product” is also used for the Cartesian product, but this has other meanings, see cross product .

The above definition is any problem (real) on classes and extensible. In particular, pairs are only formed for elements of and ; these cannot be real classes and have no special requirements for pair formation. ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle A}$ ${\displaystyle B}$

Examples

The Cartesian product of two sets consists of all possible ordered pairs of elements of the sets.

The Cartesian product of the two sets and is ${\displaystyle A\times B}$ ${\displaystyle A=\{a,b,c\}}$ ${\displaystyle B=\{x,y\}}$

${\displaystyle A\times B=\left\{(a,x),(a,y),(b,x),(b,y),(c,x),(c,y)\right\}}$.

The Cartesian product , on the other hand, is a different set, namely ${\displaystyle B\times A}$

${\displaystyle B\times A=\left\{(x,a),(x,b),(x,c),(y,a),(y,b),(y,c)\right\}}$,

because the order of the elements plays a role in ordered pairs. The Cartesian product of with itself is ${\displaystyle A}$

${\displaystyle A\times A=\left\{(a,a),(a,b),(a,c),(b,a),(b,b),(b,c),(c,a),(c,b),(c,c)\right\}}$.

The real number level arises from the Cartesian product of the real numbers with themselves: ${\displaystyle \mathbb {R} }$

${\displaystyle \mathbb {R} \times \mathbb {R} =\mathbb {R} ^{2}=\{(x,y)\mid x,y\in \mathbb {R} \}}$.

The tuples are also called Cartesian coordinates . The Cartesian product of two real intervals and gives the rectangle ${\displaystyle (x,y)}$ ${\displaystyle [a,b]}$ ${\displaystyle [c,d]}$

${\displaystyle [a,b]\times [c,d]=\{(x,y)\in \mathbb {R} ^{2}\mid a\leq x\leq b,c\leq y\leq d\}}$.

properties

Number of elements

	a	b	c	d	e	f	G	H
8th									8th
7th									7th
6th									6th
5									5
4th									4th
3									3
2									2
1									1
	a	b	c	d	e	f	G	H

A chessboard has squares identified by a pair of letters from the line and number from the row. ${\displaystyle 8^{2}=64}$

If the sets and are finite , then their Cartesian product is a finite set of ordered pairs. The number of pairs corresponds to the product of the numbers of the elements of the initial sets, that is ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle A\times B}$

${\displaystyle |A\times B|=|A|\cdot |B|}$

In the special case that is, applies ${\displaystyle A=B}$

${\displaystyle |A^{2}|=|A|^{2}}$.

If at least one of the two sets and contains an infinite number of elements and the other is not empty, then its Cartesian product consists of an infinite number of pairs. The Cartesian product of two countably infinite sets is also countable according to Cantor's first diagonal argument . If at least one of the two sets is uncountable , then its product set is also uncountable. ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle A\times B}$

Empty set

Since no element can be selected from the empty set , the Cartesian product of the empty set with any set results in the empty set. More generally applies

${\displaystyle A\times B=\emptyset ~\Longleftrightarrow ~A=\emptyset ~{\text{oder}}~B=\emptyset }$,

that is, the Cartesian product of two sets is empty if and only if at least one of the two sets is empty.

Non-commutativity

The Cartesian product is not commutative , that is, for nonempty sets and with is ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle A\neq B}$

${\displaystyle A\times B\neq B\times A}$,

for in the pairs of the set the first element is off and the second is off , while in the pairs of the set the first element is off and the second is off. There is, however, a canonical bijection between the two sets, namely ${\displaystyle A\times B}$ ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle B\times A}$ ${\displaystyle B}$ ${\displaystyle A}$

${\displaystyle A\times B\to B\times A,\quad (a,b)\mapsto (b,a)}$,

with which the quantities can be identified with one another.

Non-associativity

The Cartesian product is also non- associative , that is, for non-empty sets , and holds in general ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle C}$

${\displaystyle A\times \left(B\times C\right)\neq \left(A\times B\right)\times C}$,

because the set on the left side contains pairs whose first element is off and whose second element is a pair off , whereas the set on the right side contains pairs whose first element is a pair off and whose second element is off. Here, too, there is a canonical bijection between these two sets, namely ${\displaystyle A}$ ${\displaystyle B\times C}$ ${\displaystyle A\times B}$ ${\displaystyle C}$

${\displaystyle A\times \left(B\times C\right)\to \left(A\times B\right)\times C,\quad (a,(b,c))\mapsto ((a,b),c)}$.

Some authors identify the pairs and with the ordered triple , which also makes the Cartesian product associative. ${\displaystyle (a,(b,c))}$ ${\displaystyle ((a,b),c)}$ ${\displaystyle (a,b,c)}$

Distributivity

Illustration of the first distributive law

The following distributive laws regarding union , intersection and subtraction of sets apply to the Cartesian product :

${\displaystyle {\begin{aligned}\left(A\cup B\right)\times C&=\left(A\times C\right)\cup \left(B\times C\right)\\\left(A\cap B\right)\times C&=\left(A\times C\right)\cap \left(B\times C\right)\\\left(A\setminus B\right)\times C&=\left(A\times C\right)\setminus \left(B\times C\right)\\A\times \left(B\cup C\right)&=\left(A\times B\right)\cup \left(A\times C\right)\\A\times \left(B\cap C\right)&=\left(A\times B\right)\cap \left(A\times C\right)\\A\times \left(B\setminus C\right)&=\left(A\times B\right)\setminus \left(A\times C\right)\end{aligned}}}$

Monotony and complement

The Cartesian product behaves monotonically with respect to the formation of subsets , that is, if the sets and are not empty, then the following applies ${\displaystyle A_{1},A_{2},B_{1}}$ ${\displaystyle B_{2}}$

${\displaystyle (A_{1}\times A_{2})\subseteq (B_{1}\times B_{2})~\Longleftrightarrow ~A_{1}\subseteq B_{1}~{\text{und}}~A_{2}\subseteq B_{2}}$.

In particular, equality applies

${\displaystyle (A_{1}\times A_{2})=(B_{1}\times B_{2})~\Longleftrightarrow ~A_{1}=B_{1}~{\text{und}}~A_{2}=B_{2}}$.

If we consider the set as the basic set of and the set as the basic set of , then has the complement of in the representation ${\displaystyle B_{1}}$ ${\displaystyle A_{1}}$ ${\displaystyle B_{2}}$ ${\displaystyle A_{2}}$ ${\displaystyle A_{1}\times A_{2}}$ ${\displaystyle B_{1}\times B_{2}}$

${\displaystyle (A_{1}\times A_{2})^{\mathsf {C}}=(A_{1}^{\mathsf {C}}\times A_{2}^{\mathsf {C}})\cup (A_{1}^{\mathsf {C}}\times A_{2})\cup (A_{1}\times A_{2}^{\mathsf {C}})}$.

Further calculation rules

Cartesian products of two intervals, their intersections and their unions

It is true

${\displaystyle \left(A_{1}\cap A_{2}\right)\times \left(B_{1}\cap B_{2}\right)=\left(A_{1}\times B_{1}\right)\cap \left(A_{2}\times B_{2}\right)}$,

but in general is

${\displaystyle \left(A_{1}\cup A_{2}\right)\times \left(B_{1}\cup B_{2}\right)\supseteq \left(A_{1}\times B_{1}\right)\cup \left(A_{2}\times B_{2}\right)}$,

because the set on the left contains pairs and that are not included in the set on the right. ${\displaystyle A_{1}\times B_{2}}$ ${\displaystyle A_{2}\times B_{1}}$

Product of finitely many quantities

definition

More generally, the Cartesian product of sets is defined as the set of all - tuples , where for each one element is from the set . Formally, the multiple Cartesian product is through ${\displaystyle A_{1}\times \dotsb \times A_{n}}$ ${\displaystyle n}$ ${\displaystyle A_{1},\dotsc ,A_{n}}$ ${\displaystyle n}$ ${\displaystyle (a_{1},\dotsc ,a_{n})}$ ${\displaystyle a_{i}}$ ${\displaystyle i=1,\ldots ,n}$ ${\displaystyle A_{i}}$

${\displaystyle A_{1}\times \dotsb \times A_{n}:=\left\{(a_{1},\dotsc ,a_{n})\mid a_{i}\in A_{i}~{\text{für}}~i=1,\dotsc ,n\right\}}$

Are defined. With the help of the product symbol , the multiple Cartesian product is also through

${\displaystyle \prod _{i=1}^{n}A_{i}=A_{1}\times \dotsb \times A_{n}}$

written down. The -fold Cartesian product of a set with itself is also written as ${\displaystyle n}$ ${\displaystyle A}$

${\displaystyle A^{n}=\underbrace {A\times \dotsc \times A} _{n{\text{-mal}}}=\left\{(a_{1},\dotsc ,a_{n})\mid a_{i}\in A~{\text{für}}~i=1,\dotsc ,n\right\}}$.

Empty product

→ Main article : Empty product

The Cartesian product of zero sets is the set that contains the empty tuple as the only element , that is

${\displaystyle \prod _{i=1}^{0}A_{i}=\{()\}.}$

In particular, is for any set ${\displaystyle A}$

${\displaystyle A^{0}=\{()\}}$.

This is used when constants of a mathematical structure are viewed as zero-digit operations.

Association of all products

With denotes the union of all -fold Cartesian products of a set with itself (for all ), i.e. the set of all tuples with elements of A, including the empty tuple: ${\displaystyle A^{*}}$ ${\displaystyle n}$ ${\displaystyle A}$ ${\displaystyle n\in \mathbb {N} }$

${\displaystyle A^{*}=\bigcup _{n=0}^{\infty }A^{n}}$.

Examples

Is then is ${\displaystyle A=\left\{0,1\right\}}$

${\displaystyle A\times A\times A=A^{3}=\{(0,0,0),(0,0,1),(0,1,0),(0,1,1),(1,0,0),(1,0,1),(1,1,0),(1,1,1)\}}$.

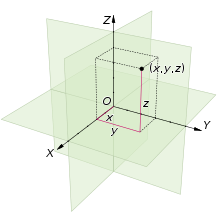
In a three-dimensional Cartesian coordinate system, each point is represented as a triplet of coordinates. ${\displaystyle (x,y,z)}$

The Euclidean space consists of three times the Cartesian product of the real numbers : ${\displaystyle \mathbb {R} ^{3}}$ ${\displaystyle \mathbb {R} }$

${\displaystyle \mathbb {R} \times \mathbb {R} \times \mathbb {R} =\mathbb {R} ^{3}=\{(x,y,z)\mid x,y,z\in \mathbb {R} \}}$.

The 3-tuples are the three-dimensional Cartesian coordinates. The Cartesian product of three real intervals , and gives the cuboid ${\displaystyle (x,y,z)}$ ${\displaystyle [a,b]}$ ${\displaystyle [c,d]}$ ${\displaystyle [e,f]}$

${\displaystyle [a,b]\times [c,d]\times [e,f]=\{(x,y,z)\in \mathbb {R} ^{3}\mid a\leq x\leq b,c\leq y\leq d,e\leq z\leq f\}}$.

In general, the -fold Cartesian product of the real numbers gives the space and the Cartesian product of real intervals gives a hyper rectangle . ${\displaystyle n}$ ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle n}$

properties

Number of elements

If the sets are all finite, then their Cartesian product is also a finite set, where the number of elements of equals the product of the element numbers of the initial sets , that is ${\displaystyle A_{1},\dotsc ,A_{n}}$ ${\displaystyle A_{1}\times \dotsb \times A_{n}}$

${\displaystyle |A_{1}\times \dotsb \times A_{n}|=|A_{1}|\cdot \ldots \cdot |A_{n}|}$

or in a different notation

${\displaystyle \left|\prod _{i=1}^{n}A_{i}\right|=\prod _{i=1}^{n}|A_{i}|}$.

In the special case that all sets are equal to one set , the following applies ${\displaystyle A_{i}}$ ${\displaystyle A}$

${\displaystyle |A^{n}|=|A|^{n}}$.

The Cartesian product of a finite number of countably infinite sets is also countable, as can be shown by iterating the argument for the Cartesian product of two sets with the help of Cantor's tuple function .

monotony

If the sets and are not empty, then, as with the Cartesian product of two sets, monotony applies ${\displaystyle A_{1},\ldots ,A_{n}}$ ${\displaystyle B_{1},\ldots ,B_{n}}$

${\displaystyle \prod _{i=1}^{n}A_{i}\subseteq \prod _{i=1}^{n}B_{i}~\Longleftrightarrow ~A_{i}\subseteq B_{i}~{\text{für}}~i=1,\ldots ,n}$

and equality

${\displaystyle \prod _{i=1}^{n}A_{i}=\prod _{i=1}^{n}B_{i}~\Longleftrightarrow ~A_{i}=B_{i}~{\text{für}}~i=1,\ldots ,n}$.

Product of infinitely many quantities

definition

It is also possible to define the Cartesian product of an infinite number of sets. If there is an index set and a family of sets for this, then the Cartesian product of the sets is defined by ${\displaystyle I}$ ${\displaystyle (A_{i})_{i\in I}}$ ${\displaystyle A_{i}}$

${\displaystyle \prod _{i\in I}A_{i}={\Big \{}f\colon I\to \bigcup _{i\in I}A_{i}\,{\Big |}\,\forall i\in I\colon f(i)\in A_{i}{\Big \}}}$.

This is the set of all images of the union of the sets for which the image in lies. If all are equal to a set , then that is the Cartesian product ${\displaystyle f}$ ${\displaystyle I}$ ${\displaystyle A_{i}}$ ${\displaystyle f(i)}$ ${\displaystyle A_{i}}$ ${\displaystyle A_{i}}$ ${\displaystyle A}$

${\displaystyle \prod _{i\in I}A=A^{I}}$

the set of all functions from to . If the quantities are different, however, the Cartesian product is much less clear. Even the question of whether any Cartesian product of non-empty sets is non-empty can not be decided with the Zermelo-Fraenkel set theory ZF; the assertion that it is not empty is a formulation of the axiom of choice which is added to ZF in order to obtain the set theory ZFC (“Zermelo-Fraenkel + Choice”). ${\displaystyle I}$ ${\displaystyle A}$ ${\displaystyle A_{i}}$

Special cases

An important special case of an infinite Cartesian product arises from the choice of natural numbers as the index set. The Cartesian product of a sequence of sets ${\displaystyle \mathbb {N} }$ ${\displaystyle (A_{i})_{i\in \mathbb {N} }=(A_{1},A_{2},\ldots )}$

${\displaystyle \prod _{i=1}^{\infty }A_{i}=\left\{(a_{1},a_{2},\dotsc )\mid a_{i}\in A_{i}~{\text{für}}~i\in \mathbb {N} \right\}}$

then corresponds to the set of all sequences whose -th sequence member is in the set . For example, if all are , then is ${\displaystyle i}$ ${\displaystyle A_{i}}$ ${\displaystyle A_{i}=\mathbb {R} }$

${\displaystyle \prod _{i=1}^{\infty }\mathbb {R} =\mathbb {R} \times \mathbb {R} \times \dotsb =\mathbb {R} ^{\mathbb {N} }=\left\{(a_{1},a_{2},\dotsc )\mid a_{i}\in \mathbb {R} ~{\text{für}}~i\in \mathbb {N} \right\}}$

the set of all real number sequences. The countable Cartesian product can be mapped bijectively onto the generally defined Cartesian product, because every sequence defines a function with and, conversely, every such function can be written as a sequence . The Cartesian product of finitely many sets can also be understood as a special case of the general definition using finite sequences. ${\displaystyle (a_{1},a_{2},\dotsc )}$ ${\displaystyle f}$ ${\displaystyle f(1):=a_{1},f(2):=a_{2},\dotsc }$ ${\displaystyle (f(1),f(2),\dotsc )}$

Universal property of the Cartesian product

The family of projections belongs to the Cartesian product . The Cartesian product together with the family has the following property: If there is an arbitrary set and is a family of images, then there is exactly one image with for all . That is, the following diagram is commutative: ${\displaystyle P=\prod \limits _{i\in I}A_{i}}$ ${\displaystyle \pi _{i}\colon \prod \limits _{i\in I}\ni \alpha \mapsto \alpha (i)\in A_{i}}$ ${\displaystyle \prod \limits _{i\in I}A_{i}}$ ${\displaystyle (\pi _{i}|i\in I)}$ ${\displaystyle X}$ ${\displaystyle f_{i}\colon X\to A_{i}}$ ${\displaystyle f\colon X\to \prod \limits _{i\in I}A_{i}}$ ${\displaystyle \pi _{i}\circ f=f_{i}}$ ${\displaystyle i\in I}$

There is exactly one , so that applies to all : ${\displaystyle f\colon X\to P}$ ${\displaystyle i\in I}$ ${\displaystyle \pi _{i}\circ f=f_{i}}$

If this quality is also common with the family , then there is a bijective mapping . ${\displaystyle Q}$ ${\displaystyle p_{i}\colon Q\to A_{i}}$ ${\displaystyle P\to Q}$

Derived terms

• A binary relation between two sets is a subset of the Cartesian product of the two sets. In particular, each mapping is therefore a subset of the Cartesian product of the definition and target set of the mapping. More generally, a -digit relation is a subset of the Cartesian product of sets. ${\displaystyle n}$ ${\displaystyle n}$
• A projection is a mapping of the Cartesian product of two sets back into one of these sets. More generally, a projection is a mapping from the Cartesian product of a family of sets onto the Cartesian product of a subfamily of these sets that selects elements with certain indices.
• A two-digit link is a mapping of the Cartesian product of two sets into another set. More generally, a -digit link is a mapping of the Cartesian product of sets into another set. Every -digit link can therefore also be understood as a -digit relation. ${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle (n+1)}$
• A direct product is a product of algebraic structures , such as groups or vector spaces , which consists of the Cartesian product of the carrier sets and is additionally provided with one or more component-wise links. A direct sum is a subset of the direct product that differs from the direct product only for products of infinitely many quantities; it consists of all tuples that differ from a certain element (usually the neutral element of a link) only in a finite number of places .
• The categorical product corresponds to the Cartesian product in the category of sets and to the direct product in the category of groups and in other categories of algebraic structures.
• In relational databases , the Cartesian product of tables and the join operations based on them are used to link database tables .

literature

• Oliver Deiser: Introduction to set theory. Georg Cantor's set theory and its axiomatization by Ernst Zermelo. 2nd improved and enlarged edition. Springer, Berlin a. a. 2004, ISBN 3-540-20401-6 .

Web links

Wikibooks: Math for non-freaks: Cartesian product  - learning and teaching materials

• M. Sh. Tsalenko: Direct product . In: Michiel Hazewinkel (Ed.): Encyclopaedia of Mathematics . Springer-Verlag , Berlin 2002, ISBN 978-1-55608-010-4 (English, online ).
• Eric W. Weisstein : Cartesian product . In: MathWorld (English).
• David Jao: Cartesian product . In: PlanetMath . (English)
• Thomas Foregger, David Jao, Andrew Archibald: Generalized cartesian product . In: PlanetMath . (English)