Group (math)

In mathematics , a group is a set of elements together with a link that assigns a third element of the same set to every two elements of the set and thereby fulfills three conditions, the group axioms : the associative law , the existence of a neutral element and the existence of inverse ones Elements .
One of the best-known groups is the set of whole numbers with addition as a link. The mathematical sub-area that is devoted to the study of group structure is called group theory . It is a branch of algebra . The areas of application of the groups, also outside of mathematics, make them a central concept of contemporary mathematics.
Groups share a fundamental kinship with the idea of symmetry . For example, the symmetry group of a geometric object embodies its symmetrical properties. It consists of the set of those images (e.g. rotations ) that leave the object unchanged, and the execution of such images as a link. Lie groups are the symmetry groups of the Standard Model of Particle Physics , point groups are used to understand symmetry at the molecular level in chemistry , and Poincaré groups can express the symmetries on which special relativity is based.
The concept of the group arose from Évariste Galois ' studies of polynomial equations in the 1830s. After contributions from other mathematical areas such as number theory and geometry , the concept of the group was generalized. It was firmly established around 1870 and is now dealt with in the independent field of group theory . To study groups, mathematicians have developed special terms to break groups down into smaller, easier-to-understand pieces, such as: B. Subgroups , Factor Groups , and Simple Groups . In addition to their abstract properties, group theorists also examine ways in which groups can be concretely expressed ( representation theory ), both for theoretical investigations and for concrete calculations. A particularly rich theory was developed for the finite groups , which culminated in 1983 in the classification of the finite simple groups . These play a comparable role for groups as the prime numbers for natural numbers .
Introductory example
One of the most well-known groups is the set of integers , usually referred to as, together with addition .
The set of whole numbers together with the addition fulfills some basic properties:
- For two whole numbers and the sum is again a whole number. If, on the other hand, one were to divide two whole numbers with one another , the result would mostly be a rational number and not a whole number. Since this cannot happen with addition, it is said that the whole numbers under addition are complete.
- For all integers , and the associative law applies
- .
- In words, it means that it doesn't matter whether you add and or and first , the result is the same. This property is called associativity .
- The following applies to every whole number
- .
- The addition with zero does not change the initial number. That is why zero is called the neutral element of addition.
- For every integer there is an integer such that . This means that for every integer there is an integer so that their sum equals zero. In this case the number is called the inverse element of and is noted with .
These four properties of the set of integers together with their addition are generalized in the definition of the group to other sets with an appropriate operation .
definition
group
A group is a pair consisting of an amount and an inner two-digit shortcut on . The figure (written in infix notation ) fulfills
the following requirements , called group axioms :
|
( Associativity ) |
|
(Existence of the neutral element) |
|
(Existence of the inverse element) |
So a group is a monoid in which each element has an inverse.
Weak group axioms
The group axioms can be formally weakened by replacing the axioms for the neutral and the inverse element as follows:
There is a left-neutral element so that:
- The following applies to all group elements :
- For each there is a left-inverse element with .
This formally weaker definition is equivalent to the original definition.
| proof |
|
It satisfies the weak group axioms. Then there is a left inverse for each group element and in turn has a left inverse . So , whatever a right inverse also applies to . This means that it is also a right-neutral element and thus also a group according to the stronger axiomatics. ∎ |
Group as an algebraic structure
A group can also be defined as a particular algebraic structure . With the weak group axioms we then get:
A group is a quadruple composed of an amount and an associative, inner two-digit shortcut , a zero-digit shortcut , and a single digit shortcut on , so that for each valid and .
Thus a group is a special monoid in which all elements are invertible.
Abelian group
A group is called Abelian or commutative if the following axiom is also fulfilled:
- Commutativity : applies toall group elementsand.
Otherwise, d. i.e., if there are group elements for which is, the group is called non-Abelian (or non-commutative ).
Group order
In a group , the thickness is also referred to as the order of the group. So for a finite group the order is simply the number of group elements.
Order of an element
The order of an element is defined by , where the neutral element represents the group .
Remarks:
- In each group, exactly the neutral element has order 1.
- The following applies to finite groups :
- (spoken: the order of divides the group order )
Notes on the notation
The symbol is often used for the link ; one then speaks of a multiplicatively written group. The neutral element is then called the unity element and is also symbolized by. As is common with ordinary multiplication , the painting point can be left out in many situations . The product symbol is then used to link several elements . For the -fold connection of a group element with itself is written as a power and one defines as well .
The group properties can also be noted additively by using the symbol for the link . The neutral element is then called the zero element and is symbolized by. The element that is inverse to the group element is not symbolized by but by in a group written in additive . A -fold sum is denoted here with and you bet as well . In this way, an Abelian group can be understood as a module over the ring of whole numbers . The additive notation is only common for Abelian groups, while non-Abelian or any groups are usually written multiplicatively.
If the connection is clear from the context, one often only writes for the group .
Examples
Some examples of groups are given below. Groups of numbers , a group with exactly one element and examples of cyclic groups are given . Further examples of groups can be found in the list of small (finite) groups .
Sets of numbers
- The set of whole numbers together with the addition forms an (Abelian) group. Together with the multiplication, however , the set of integers is not a group (the inverse element of 2 would be 1/2).
- The set of rational numbers or the set of real numbers together with the addition is a group. Together with the multiplication, the quantities and are also groups.
The trivial group
The set that has only one element can be viewed as a group. Since every group has a neutral element, exactly this one element must then be understood as the neutral element. So then applies . The remaining group axioms can also be proved by means of this equality. The group with exactly one element is called the trivial group.
Cyclic groups
A cyclic group is a group whose elements can be represented as the power of one of its elements. Using multiplicative notation, the elements of a cyclic group are
- ,
where means and denotes the neutral element of the group. The element is called the producer or the primitive root of the group. In additive notation, an element is a primitive root when the elements of the group go through
can be represented.
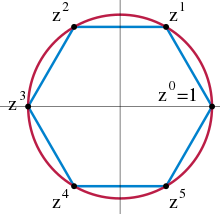
For example, the additive group of integers considered in the first section is a cyclic group with the primitive root . This group has an infinite number of elements . In contrast, the multiplicative group of the nth complex roots of unity has finitely many elements . This group consists of all the complex numbers that make up the equation
fulfill. The group elements can be visualized as corner points of a regular n corner . For this has been done in the graph on the right. The group operation is the multiplication of the complex numbers. In the right picture so the multiplication corresponds to the rotation of the polygon in counterclockwise order .
Cyclic groups have the property of being clearly defined by the number of their elements. That is, two cyclic groups each with elements are isomorphic , so a group isomorphism can be found between these two groups. In particular, all cyclic groups with an infinite number of elements are equivalent to the cyclic group of whole numbers.
Symmetrical groups
→ Main article: Symmetric group
The symmetric group consists of all permutations (exchanges) of a -element set . The group operation is the composition (execution) of the permutations, the neutral element is the identical mapping . The symmetric group is finite and has the order . It is for not abelian.
Basic characteristics of a group
- The neutral element of a group is clearly defined. Namely, if and are neutral elements, then there must be, da is neutral and , da is neutral. So it follows .
- The abbreviation rule applies: From or with the group elements follows in each case . You can see this through
- .
- From this it follows that the linking table of a (finite) group is a Latin square in which every group element occurs exactly once in every row and in every column.
- The equation is always uniquely solvable and the solution is . Likewise has the clear solution .
- The element inverse to a group element is clearly defined. If and both are inverse to then it follows:
- It applies and .
- The following applies to all elements . This follows from the chain of equations
- .
- So is too inverse.
Group homomorphism
Group homomorphisms are images that preserve the group structure. An illustration
between two groups and is called group homomorphism or homomorphism for short, if the equation
applies to all elements . If the mapping is also bijective , it is called group isomorphism. In this case the groups are called and isomorphic to each other.
With the group homomorphisms as morphisms , the class of all groups forms a category that is usually referred to as Grp or Gr .
Opposing group
For each group , the leaves opposite group formed by in linking the operands against reversed:
- for all (same basic amount ).
Is Abelian, so is .
is the counter group of the counter group of the group : .
An antihomomorphism between two groups is a homomorphism respectively .
Products by groups
In group theory, different products of groups are considered:
- The direct product is given by the Cartesian product of the carrier quantities together with the component-wise link.
- The semi-direct product is a generalization of the direct product, with one group operating on the second. It can also be implemented as an inner semi-direct product between a normal divisor and a subgroup of a given group.
- The wreath product is a special semi-direct product.
- The complex product of two subgroups of a given group is given by linking the subgroup elements in pairs. This product is more generally useful for any two subsets of the group.
- The free product represents the categorical co- product in the category of groups.
- The amalgamated product is a generalization of the free product in which the elements of a common subgroup are fused together ("amalgamated").
Individual evidence
- ↑ George G. Hall: Applied group theory . American Elsevier, New York 1967, p. 1.
- ^ Heinz-Wilhelm Alten : 4000 years of algebra. History, cultures, people . Springer, Berlin a. a. 2003, ISBN 3-540-43554-9 , pp. 358 .
- ^ Siegfried Bosch : Algebra . 6th edition. Springer-Verlag, 2006, ISBN 3-540-40388-4 , p. 11.
- ↑ This means that the spelling without brackets is well defined .
- ↑ The requirement of uniqueness is redundant, because from the stipulation follows: If a neutral element, then is
- ↑ The requirement of uniqueness is redundant, because from the stipulation follows: If an element is too inverse, then is
- ^ Siegfried Bosch: Linear Algebra . 3. Edition. Springer textbook, Heidelberg 2006, ISBN 3-540-29884-3 , pp. 14 .
- ^ Siegfried Bosch: Algebra . 6th edition. Springer-Verlag, 2006, ISBN 3-540-40388-4 , pp. 11-12.
- ↑ Gerd Fischer : Textbook of Algebra . 1st edition. Vieweg, Wiesbaden 2008, ISBN 978-3-8348-0226-2 , p. 6.
- ^ Siegfried Bosch: Algebra . 6th edition. Springer-Verlag, 2006, ISBN 3-540-40388-4 , p. 13.
- ^ Nicolas Bourbaki , Eléments de mathématique , Algèbre , ch. I, § 4, n ° 1; Paris, Hermann, 1970, p.29.
- ↑ PlanetMath.org Opposite Group