Root of unity

The title of this article is ambiguous. For the meaning of unit root in time series analysis, see unit root (time series analysis) .

In algebra , numbers whose -th power is 1 are called -th roots of unity . ${\displaystyle n}$ ${\displaystyle n}$

definition

Let it be a commutative ring with a one element and a natural number . An element is called a -th root of unity if it fulfills one of the two equivalent conditions: ${\displaystyle R}$ ${\displaystyle n\geq 1}$ ${\displaystyle \zeta \in R}$ ${\displaystyle n}$

• ${\displaystyle \zeta ^{n}=1}$
• ${\displaystyle \zeta }$is the root of the polynomial ${\displaystyle X^{n}-1}$

The -th roots of unity in form a subgroup of the multiplicative group , which is often referred to as. ${\displaystyle n}$ ${\displaystyle R}$ ${\displaystyle R^{\times }}$ ${\displaystyle \mu _{n}(R)}$

A -th root of unity is called primitive if for . ${\displaystyle n}$ ${\displaystyle \zeta }$ ${\displaystyle \zeta ^{m}\neq 1}$ ${\displaystyle m=1,\dotsc ,n-1}$

Unity roots in complex numbers

In the body of the complex numbers are ${\displaystyle \mathbb {C} }$

${\displaystyle \exp \left({\frac {2\pi \mathrm {i} \,k}{n}}\right),\quad k=0,1,\dotsc ,n-1}$

the -th roots of unity, where is the imaginary unit . If you set ${\displaystyle n}$ ${\displaystyle \mathrm {i} }$

${\displaystyle \zeta _{n}=\exp \left({\frac {2\pi \mathrm {i} }{n}}\right)}$,

so is primitive, and these numbers get (in the same order) the simple form ${\displaystyle \zeta _{n}}$

${\displaystyle 1,\zeta _{n},\zeta _{n}^{2},\dotsc ,\zeta _{n}^{n-1}}$.

If it is clear what it is, the lower index is often dropped. ${\displaystyle n}$

Group of roots of unity

Since and with and are also roots of unity, the set of all roots of unity is a group. The image ${\displaystyle 1}$ ${\displaystyle \zeta _{n}^{i}}$ ${\displaystyle \zeta _{m}^{j}}$ ${\displaystyle \zeta _{n}^{i}\zeta _{m}^{j}=\zeta _{nm}^{im+jn}}$ ${\displaystyle \mu (\mathbb {C} )}$

${\displaystyle f\colon \mathbb {Q} \to \mu (\mathbb {C} ),\quad {\dfrac {k}{n}}\mapsto \exp \left({\dfrac {2\pi \mathrm {i} \,k}{n}}\right)}$

is surjective. The gist of this figure is . The group of complex roots of unity is therefore isomorphic to the factor group . ${\displaystyle \mathbb {Z} }$ ${\displaystyle \mathbb {Q} /\mathbb {Z} }$

Geometric reference

The -th roots of unit can be interpreted in a geometrically clear manner in the complex number plane : They are the corners of a regular corner lying on the unit circle (with center 0 and radius 1) , where one of the corners is the number , because this is for each one - te root of unity. ${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle 1}$ ${\displaystyle n\geq 1}$ ${\displaystyle n}$

The real part and the imaginary part of the roots of unit are thus the coordinates of the corners of the corner on the circle, i.e. H. for is ${\displaystyle \zeta _{n}^{k}=x_{k}+\mathrm {i} \,y_{k}}$ ${\displaystyle n}$ ${\displaystyle k=0,1,\dotsc ,n-1}$

${\displaystyle x_{k}=\cos(2\pi k/n)=\cos(360^{\circ }\cdot k/n)}$    and    . ${\displaystyle y_{k}=\sin(2\pi k/n)=\sin(360^{\circ }\cdot k/n)}$

For more see Extracting Complex Numbers .

Sum of the roots of unity

If there is a -th root of unity, then applies ${\displaystyle \zeta }$ ${\displaystyle n}$

${\displaystyle 1+\zeta +\zeta ^{2}+\dotsb +\zeta ^{n-1}={\begin{cases}n&\mathrm {falls} \ \zeta =1\\0&\mathrm {sonst} .\end{cases}}}$

This statement follows directly from the geometrical sum formula and is a special case of the analogous statement for characters of groups .

Examples

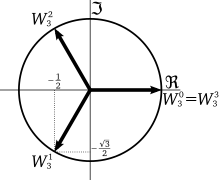
The second, third and fourth roots of unity

The function ${\displaystyle z\mapsto z^{3}-1}$

The third roots of unity

The second roots of unity are

${\displaystyle \zeta _{1}=-1,\quad \zeta _{2}=1}$;

are the third roots of unity

${\displaystyle \zeta _{1}=-{\frac {1}{2}}+{\frac {\mathrm {i} }{2}}{\sqrt {3}},\quad \zeta _{2}=-{\frac {1}{2}}-{\frac {\mathrm {i} }{2}}{\sqrt {3}},\quad \zeta _{3}=1}$;

the fourth roots of unity are again of a simpler form:

${\displaystyle \zeta _{1}=\mathrm {i} ,\quad \zeta _{2}=-1,\quad \zeta _{3}=-\mathrm {i} ,\quad \zeta _{4}=1}$.

The fifth roots of unity

The function ${\displaystyle z\mapsto z^{5}-1}$

The fifth roots of unity

From follows ${\displaystyle 0=1+\zeta +\zeta ^{2}+\zeta ^{3}+\zeta ^{4}}$

${\displaystyle 0={\frac {1}{\zeta ^{2}}}+{\frac {1}{\zeta }}+1+\zeta +\zeta ^{2}=\left({\zeta }+{\frac {1}{\zeta }}\right)^{2}+\left({\zeta }+{\frac {1}{\zeta }}\right)-1=w^{2}+w-1}$

for . Solving this quadratic equation yields . Since the angle is in the 1st quadrant, is positive, and thus is the real part of . The imaginary part is according to the Pythagorean theorem . ${\displaystyle w=\zeta +{\frac {1}{\zeta }}=\zeta +\zeta ^{4}=2\cos(72^{\circ })}$ ${\displaystyle w=-{\frac {1}{2}}\pm {\sqrt {\frac {5}{4}}}}$ ${\displaystyle 72^{\circ }}$ ${\displaystyle w}$ ${\displaystyle \cos(72^{\circ })={\frac {{\sqrt {5}}-1}{4}}}$ ${\displaystyle \zeta }$ ${\displaystyle \sin(72^{\circ })={\sqrt {\frac {{\sqrt {5}}+5}{8}}}}$

Properties of the roots of unity

Roots of unity in (commutative) bodies

Is the characteristic of the body , then is a -fold zero of the polynomial . If it is not a divisor of the order , then the following statements also apply to fields with prime number characteristics . For additional properties of the roots of unity in such fields see Finite Field # Multiplicative Group and Discrete Logarithm . ${\displaystyle p:=\operatorname {char} (K)\neq 0}$ ${\displaystyle K}$ ${\displaystyle \zeta =1}$ ${\displaystyle p}$ ${\displaystyle X^{p}-1}$ ${\displaystyle p}$ ${\displaystyle n}$ ${\displaystyle p}$

• If a ( commutative ) field is and , then the elements with form a cyclic subgroup of the multiplicative group . ${\displaystyle K}$ ${\displaystyle n\in \mathbb {N} }$ ${\displaystyle \zeta \in K}$ ${\displaystyle \zeta ^{n}=1}$ ${\displaystyle U}$ ${\displaystyle K^{\times }}$
• The group order of is always a factor of . ${\displaystyle U}$ ${\displaystyle n}$
• If it is the same , it is said that “contains the -th roots of unity” and is called “the group of -th roots of unity”. ${\displaystyle n}$ ${\displaystyle K}$ ${\displaystyle n}$ ${\displaystyle U}$ ${\displaystyle n}$
• A th root of unity if and primitive, when the group of th roots of unity produced . The order of a primitive -th root of unity is . The primitive -th roots of unity are exactly the zeros of the -th circle division polynomial . ${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle \zeta _{n}}$ ${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle n}$
• Is a primitive -th root of unity, then is a primitive -th root of unity ( greatest common factor ). ${\displaystyle \zeta _{n}}$ ${\displaystyle n}$ ${\displaystyle \zeta _{n}^{k}}$ ${\displaystyle {\frac {n}{\operatorname {ggT} (k,n)}}}$
• The number of primitive -th roots of unity is ( Euler's phi function ). ${\displaystyle n}$ ${\displaystyle \varphi (n)}$
• Extensions of which arise through the adjunction of roots of unity are called circle dividing bodies . ${\displaystyle \mathbb {Q} }$
• A finite multiplicative subgroup of a ( commutative ) field is cyclic . ${\displaystyle U}$ ${\displaystyle K}$

Proof of the last statement: is an Abelian torsion group . So she is a direct product ${\displaystyle U}$

${\displaystyle U=\prod _{p\in \mathbb {P} }U_{(p)}}$   With   ${\displaystyle U_{(p)}:=\left\{u\in U\left|\;\bigvee _{i\in \mathbb {N} }(u^{p^{i}}=1)\right.\right\}}$

isomorphic (  : = set of positive prime numbers). And they are cyclical because the group elements of the order are all zeros of and thus powers of one another. Finally, because of the coprime nature of powers of different prime numbers, the direct product is cyclic. ${\displaystyle \mathbb {P} }$ ${\displaystyle U_{(p)}}$ ${\displaystyle p^{i}}$ ${\displaystyle X^{p^{i}}-1}$

Example of roots of unity in non-commutative (skew) fields

In the non-commutative inclined body of the quaternions , the polynomial has the infinite number of zeros ${\displaystyle \mathbb {H} }$ ${\displaystyle X^{2}-1}$

${\displaystyle \epsilon =\epsilon _{0}+\epsilon _{1}\mathrm {i} +\epsilon _{2}\mathrm {j} +\epsilon _{3}\mathrm {k} }$

With

${\displaystyle \epsilon _{0}=0\;\land \;\epsilon _{1}^{2}+\epsilon _{2}^{2}+\epsilon _{3}^{2}=1}$.

The quaternion group is a finite non-commutative subgroup of the multiplicative group . It has order 8 and the exponent 4. For further finite subgroups of see Quaternion # The finite subgroups . ${\displaystyle \mathbb {H} ^{\times }}$ ${\displaystyle \mathbb {H} ^{\times }}$

Roots of unity in residue class rings

• In the ring of whole numbers modulo the number is a primitive -th root of unity, because in this ring applies . ${\displaystyle \mathbb {Z} _{2^{n}+1}=\mathbb {Z} /(2^{n}+1)\mathbb {Z} }$ ${\displaystyle (2^{n}+1)}$ ${\displaystyle 2}$ ${\displaystyle 2n}$ ${\displaystyle 2^{n}=-1}$
• In the ring of whole numbers modulo , the number is a primitive -th root of unity. ${\displaystyle \mathbb {Z} _{2^{n}-1}=\mathbb {Z} /(2^{n}-1)\mathbb {Z} }$ ${\displaystyle (2^{n}-1)}$ ${\displaystyle 2}$ ${\displaystyle n}$

These two special residual class rings are extremely important for computer algebra , because they enable a variant of the fast discrete Fourier transformation that is again drastically accelerated . The reason for this is that addition and multiplication of these remainder class rings can be replaced by corresponding cyclic addition and multiplication in an insignificantly larger remainder class ring, and thus in binary number representation the multiplication by powers of the number means a cyclical binary shift operation, which can be carried out much faster as a general multiplication of two numbers. The considerable time saving for the discrete Fourier transformation results from the fact that many multiplications with the selected unit root have to be carried out during the fast Fourier transformation. ${\displaystyle 2}$

literature

• Siegfried Bosch : Algebra. 7th edition. Springer-Verlag, Berlin 2009, ISBN 978-3-540-92811-9 , Section 4.5 ( limited preview in the Google book search).