Geometric series

The geometric series for , or converges. ${\displaystyle \sum _{k=0}^{\infty }r^{k}}$ ${\displaystyle r={\tfrac {1}{2}}}$ ${\displaystyle r={\tfrac {1}{3}}}$ ${\displaystyle r={\tfrac {1}{4}}}$

A geometric series is the series of a geometric sequence . In the case of a geometric sequence, the quotient of two adjacent sequence members is constant. for true ${\displaystyle q}$ ${\displaystyle |q|<1}$

${\displaystyle \sum _{k=0}^{\infty }a_{0}q^{k}={\frac {a_{0}}{1-q}}}$

A starting value of the geometric sequence of 1 and a quotient greater than 1 (here 2) results in a diverging geometric series: 1, 1 + 2, 1 + 2 + 4, 1 + 2 + 4 + 8, ..., so in summary 1, 3 , 7, 15, ...

With an identical start value and a quotient of 1/2, however, the geometric series results: 1, 1 + 1/2, 1 + 1/2 + 1/4, 1 + 1/2 + 1/4 + 1/8, ... , i.e. 1, 3/2, 7/4, 15/8, ... with the limit value . ${\displaystyle {\tfrac {1}{1-1/2}}=2}$

Calculation of the (finite) partial sums of a geometric series

By definition, a series is a sequence of partial sums. The value of the series is the limit of this series of partial sums. A finite sum is thus a sequence member from the sequence of partial sums. The (finite) sum of the first terms of a series is called the -th partial sum and not a “partial series” or the like. ${\displaystyle n}$ ${\displaystyle n}$

A geometrical sequence is given . ${\displaystyle (a_{k})_{k\in \mathbb {N} _{0}}}$

${\displaystyle s=\sum _{k=0}^{\infty }a_{k}\quad }$ is the associated geometric series.

We can make a new episode from this

${\displaystyle (s_{n})=\left(\sum _{k=0}^{n}a_{k}\right)=\left(\sum _{k=0}^{0}a_{k},\sum _{k=0}^{1}a_{k},\sum _{k=0}^{2}a_{k},\sum _{k=0}^{3}a_{k},\ldots \right)=\left(a_{0},a_{0}+a_{1},a_{0}+a_{1}+a_{2},a_{0}+a_{1}+a_{2}+a_{3},\ldots \right)}$

construct whose -th term is the sum of the first terms of the series , the so-called -th partial sum of . This sequence is called the sequence of the partial sums . (Strictly speaking, the series is defined in reverse order on the basis of the partial sums of a sequence. The above and usual notation for the series does not provide that, so we must first reconstruct the sequence of the partial sums from it.) If it converges, becomes over it defines the value of the series . The following applies to the value of the series s (here we no longer speak of "limit value"): ${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle s}$ ${\displaystyle n}$ ${\displaystyle s}$ ${\displaystyle s}$ ${\displaystyle s}$

${\displaystyle s:=\lim _{n\to \infty }s_{n};}$

In words: The value of the series is defined as the limit value of the partial sum sequence belonging to it, if this converges, otherwise the series is called divergent . If in this case the sequence of the partial sums tends towards (plus / minus) infinity, one usually writes or and says that the sequence converges towards the improper limit value (plus / minus) infinity or the series has the improper value (plus / minus) infinity . (A calculation formula for the limit value follows below.) ${\displaystyle s}$ ${\displaystyle s=\lim _{n\to \infty }s_{n}=\infty }$ ${\displaystyle {-}\infty }$

With we now denote the ratio of two neighboring terms, which is the same for all . ${\displaystyle q}$ ${\displaystyle a_{k+1}/a_{k}}$ ${\displaystyle k}$

Then applies to everyone . ${\displaystyle a_{k}=a_{0}q^{k}}$ ${\displaystyle k}$

For the -th partial sum we get: ${\displaystyle n}$ ${\displaystyle s_{n}}$

${\displaystyle s_{n}=a_{0}\sum _{k=0}^{n}q^{k}}$

If so , then ( derivation see below) ${\displaystyle q\neq 1}$

${\displaystyle s_{n}=a_{0}{\frac {q^{n+1}-1}{q-1}}=a_{0}{\frac {1-q^{n+1}}{1-q}}}$

If so, then ${\displaystyle q=1}$

${\displaystyle s_{n}=a_{0}(n+1)}$

The above applies if the sequence members are elements of a unitary ring , i.e. especially if they are real numbers .

Related empirical formula 1

The partial sum

${\displaystyle s_{n}=\sum _{k=0}^{n}a_{0}q^{k}k}$

has for the result ${\displaystyle q\neq 1}$

${\displaystyle s_{n}=a_{0}{\frac {nq^{n+2}-(n+1)q^{n+1}+q}{(q-1)^{2}}}}$

and for (see Gaussian empirical formula ) ${\displaystyle q=1}$

${\displaystyle s_{n}=a_{0}\sum _{k=0}^{n}1^{k}k=a_{0}\sum _{k=0}^{n}1k=a_{0}\sum _{k=0}^{n}k=a_{0}{\frac {n(n+1)}{2}}}$;

this formula also results from the formula for (with double application of de l'Hospital's rule ) as its limit value for . ${\displaystyle q\neq 1}$ ${\displaystyle q\to 1}$

Related empirical formula 2

The partial sum

${\displaystyle s_{n}=\sum _{k=0}^{n}a_{0}q^{k}k^{2}}$

has for the result ${\displaystyle q\neq 1}$

${\displaystyle s_{n}=a_{0}{\frac {n^{2}q^{n+3}-(2n^{2}+2n-1)q^{n+2}+(n+1)^{2}q^{n+1}-q^{2}-q}{(q-1)^{3}}}}$

and for (see power sums ) ${\displaystyle q=1}$

${\displaystyle s_{n}=a_{0}{\frac {n(n+1)(2n+1)}{6}}}$

Examples

Numerical example

Let the geometric sequence be given

${\displaystyle a_{0}=5,\ a_{1}=15,\ a_{2}=45,\ a_{3}=135,\ \dotsc }$

with and The corresponding geometric series is ${\displaystyle a_{0}=5}$ ${\displaystyle q=3.}$

${\displaystyle s=\sum _{k=0}^{\infty }5\cdot 3^{k}=5+15+45+135+\dotsb =\infty }$

The associated sequence of partial sums results in

${\displaystyle s_{0}=5=5{\frac {1-3^{1}}{1-3}}}$

${\displaystyle s_{1}=5+15=20=5{\frac {1-3^{2}}{1-3}}}$

${\displaystyle s_{2}=5+15+45=65=5{\frac {1-3^{3}}{1-3}}}$

${\displaystyle s_{3}=5+15+45+135=200=5{\frac {1-3^{4}}{1-3}}}$

etc.

Pension bill

Suppose you deposit € 2000 in a bank at the beginning of each year and the interest rate is 5% [i.e. H. the interest factor is: ]. How much money do you have at the end of the fifth year? ${\displaystyle 1+(5/100)=1{,}05}$

The paid in the first year money will earn interest for five years, you score at the end, including compound interest 2000 · 1.05 ⁵ €. The money deposited in the second year only earns interest for four years and so on. In total, the pension calculation results in a saved amount of

${\displaystyle {\begin{aligned}&2\,000\cdot 1{,}05^{5}+2\,000\cdot 1{,}05^{4}+2\,000\cdot 1{,}05^{3}+2\,000\cdot 1{,}05^{2}+2\,000\cdot 1{,}05^{1}\\&\quad =2\,000\cdot 1{,}05\cdot (1{,}05^{4}+1{,}05^{3}+1{,}05^{2}+1{,}05^{1}+1{,}05^{0})\\&\quad =2\,000\cdot 1{,}05\cdot \sum _{k=0}^{4}1{,}05^{k}\\&\quad =2\,000\cdot 1{,}05\cdot {\frac {1{,}05^{4+1}-1}{1{,}05-1}}\\&\quad =2\,000\cdot 1{,}05\cdot {\frac {1{,}05^{5}-1}{0{,}05}}\\&\quad =11\,603{,}826\end{aligned}}}$

As a result of interest, the capital has thus increased by € 1603.83. When recalculating bank statements, it should be noted that in banking, mathematical rounding is not used.

For comparison: If € 2,000 were not paid in year after year, but the whole € 10,000 were invested over 5 years at 5% interest right from the start, the final amount would be

${\displaystyle 10\,000\cdot 1{,}05^{5}=12\,762{,}8156}$

thus an investment income of € 2762.82.

In general, if the deposit is at the beginning of each year , the interest factor and the term are years, then the final value is ${\displaystyle a_{0}}$ ${\displaystyle q}$ ${\displaystyle n}$

${\displaystyle \sum _{k=1}^{n}a_{0}q^{k}=a_{0}q{\frac {q^{n}-1}{q-1}}}$.

Pension calculation with linear dynamics

In contrast to the previous example, if you do not pay a fixed annual contribution , but from the 2nd year onwards each year more than in the previous year ( linear dynamics ), then the final value is ${\displaystyle a_{0}}$ ${\displaystyle d}$

${\displaystyle {\begin{aligned}&\sum _{k=1}^{n}q^{k}(a_{0}+d(n-k))=\sum _{k=1}^{n}(q^{k}(a_{0}+dn)-q^{k}dk)\\&\qquad =\left(\sum _{k=1}^{n}q^{k}(a_{0}+dn)\right)-\left(\sum _{k=1}^{n}q^{k}dk\right)\\&\qquad =(a_{0}+dn)\left(\sum _{k=1}^{n}q^{k}\right)-d\left(\sum _{k=1}^{n}q^{k}k\right)\\&\qquad =(a_{0}+dn){\frac {q^{n+1}-q}{q-1}}-d{\frac {nq^{n+2}-(n+1)q^{n+1}+q}{(q-1)^{2}}}\end{aligned}}}$

For example, with  € in the first year, every year  € more than in the previous year, 5% interest (i.e. interest factor ) and years of maturity, then the amount saved at the end of the 5th year ${\displaystyle a_{0}=2.000}$ ${\displaystyle d=100}$ ${\displaystyle q=1{,}05}$ ${\displaystyle n=5}$

${\displaystyle {\begin{aligned}&(2\,000+100\cdot 5)\cdot {\frac {1{,}05^{5+1}-1{,}05}{1{,}05-1}}-100\cdot {\frac {5\cdot 1{,}05^{5+2}-(5+1)\cdot 1{,}05^{5+1}+1{,}05}{(1{,}05-1)^{2}}}\\&\qquad =2\,500\cdot {\frac {0{,}29}{0{,}05}}-100\cdot {\frac {7{,}03-8{,}04+1{,}05}{0{,}0025}}\\&\qquad =2\,500\cdot 5{,}8-100\cdot {\frac {0{,}0449}{0{,}0025}}\\&\qquad =14\,504{,}78-100\cdot 17{,}97\\&\qquad =12\,707{,}65\end{aligned}}}$

In this example, instead of € 10,000, but a total of € 11,000, the profit is € 1,707.65. If you  only deposit € instead of  € in the first year and leave the other factors the same (so that you deposit a total of € 10,000 as in the penultimate example), then the final value is only € 11,547.27, i.e. you pay in the same amount, only At the beginning less, but more later, then you miss out on profits ( opportunity costs ). ${\displaystyle a_{0}=2.000}$ ${\displaystyle a_{0}=1.800}$

Periodic decimal fractions

Periodic decimal fractions contain a geometric series that can be converted back into a fraction using the above formulas.

Example 1:

${\displaystyle {\begin{aligned}0{,}2{\overline {67}}&={\frac {2}{10}}+{\frac {67}{1000}}\cdot \sum _{k=0}^{\infty }({\frac {1}{100}})^{k}={\frac {2}{10}}+{\frac {67}{1000}}\cdot {\frac {1}{1-{\frac {1}{100}}}}\\&={\frac {2}{10}}+{\frac {67}{1000}}\cdot {\frac {100}{99}}={\frac {2}{10}}+{\frac {67}{990}}={\frac {265}{990}}={\frac {53}{198}}\end{aligned}}}$

Example 2:

${\displaystyle 0{,}{\overline {9}}={\frac {9}{10}}+{\frac {9}{100}}+{\frac {9}{1000}}+\,\ldots ={\frac {9}{10}}\cdot \sum _{k=0}^{\infty }({\frac {1}{10}})^{k}={\frac {9}{10}}\cdot {\frac {1}{1-{\frac {1}{10}}}}={\frac {9}{10}}\cdot {\frac {10}{9}}=1}$

Convergence and value of the geometric series

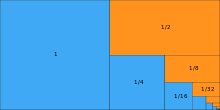
Convergence of the geometric series for q = 1/2

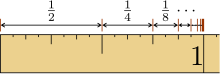
Convergence of the geometric series on the number line

A geometric series or the sequence of its partial sums converges if the absolute value of the real (or complex ) number is less than one or its initial term is zero. For or the underlying geometric sequence converges to zero: ${\displaystyle q}$ ${\displaystyle a_{0}}$ ${\displaystyle \|q\|<1}$ ${\displaystyle a_{0}=0}$

${\displaystyle \lim _{k\to \infty }a_{0}q^{k}=0}$.

According to the zero sequence criterion , this is a necessary condition for the convergence of the geometric series. Since for and the basic sequence diverges, in this case there is also divergence of the series. ${\displaystyle |q|>1}$ ${\displaystyle a_{0}\neq 0}$

For the divergence of the geometric series results from ${\displaystyle q=1}$

${\displaystyle \sum _{k=0}^{N}a_{0}q^{k}=\sum _{k=0}^{N}a_{0}\cdot 1=(N+1)\cdot a_{0}}$,

an expression that diverges for and . ${\displaystyle N\to \infty }$ ${\displaystyle a_{0}\neq 0}$

For the case , the divergence always results as a certain divergence (see above), for the case always as an indefinite divergence . The geometric series also converges absolutely if it converges in the normal way. ${\displaystyle q>1}$ ${\displaystyle q\leq -1}$

The value of the series in the case of convergence results from the above formula for the -th partial sums by forming the limit ( ) for to ${\displaystyle n}$ ${\displaystyle n\to \infty }$ ${\displaystyle |q|<1}$

${\displaystyle \sum _{k=0}^{\infty }a_{0}q^{k}=\lim _{n\to \infty }\sum _{k=0}^{n}a_{0}q^{k}=\lim _{n\to \infty }a_{0}{\frac {1-q^{n+1}}{1-q}}={\frac {a_{0}}{1-q}},}$

because it is ${\displaystyle \lim _{n\to \infty }(1-q^{n+1})=1.}$

The last formula is even valid in any Banach algebra as long as the norm is less than one; in the context of linear operators one also speaks of the Neumann series . ${\displaystyle q}$

Derivations

Play media file

Song by DorFuchs with a derivation of the equation for the geometric series

Derivation of the formula for the partial sums

The -th partial sum of the geometric series can be calculated as follows: ${\displaystyle n}$

${\displaystyle s_{n}=\sum _{k=0}^{n}a_{0}q^{k}=a_{0}+a_{0}q+a_{0}q^{2}+\dotsb +a_{0}q^{n}}$

Simplified:

${\displaystyle s_{n}=a_{0}(1+q+q^{2}+\dotsb +q^{n})}$   (Equation 1)

Multiplication with gives: ${\displaystyle q}$

${\displaystyle qs_{n}=a_{0}(q+q^{2}+q^{3}+\dotsb +q^{n+1})}$   (Equation 2)

Subtracting equation 2 from equation 1 gives:

${\displaystyle s_{n}-qs_{n}=a_{0}(1-q^{n+1})}$

Excluding : ${\displaystyle s_{n}}$

${\displaystyle s_{n}(1-q)=a_{0}(1-q^{n+1})\ }$

Divide by gives the formula for the partial sums you are looking for: ${\displaystyle (1-q)}$ ${\displaystyle q\neq 1}$

${\displaystyle s_{n}=a_{0}{{1-q^{n+1}} \over {1-q}}}$

Derivation of the variants

With the help of the formula given above, the following finite series can also be represented in a closed manner through member-wise differentiation ${\displaystyle q\neq 1}$

${\displaystyle {\begin{aligned}\sum _{k=0}^{n}kq^{k}&=\sum _{k=0}^{n}q{\frac {\mathrm {d} }{\mathrm {d} q}}q^{k}=q{\frac {\mathrm {d} }{\mathrm {d} q}}\sum _{k=0}^{n}q^{k}=q{\frac {\mathrm {d} }{\mathrm {d} q}}{\frac {1-q^{n+1}}{1-q}}\\&={\frac {nq^{n+2}-(n+1)q^{n+1}+q}{(1-q)^{2}}}\end{aligned}}}$

${\displaystyle {\begin{aligned}\sum _{k=0}^{n}k^{2}q^{k}&=\sum _{k=0}^{n}q{\frac {\mathrm {d} }{\mathrm {d} q}}q{\frac {\mathrm {d} }{\mathrm {d} q}}q^{k}=q{\frac {\mathrm {d} }{\mathrm {d} q}}q{\frac {\mathrm {d} }{\mathrm {d} q}}\sum _{k=0}^{n}q^{k}=q{\frac {\mathrm {d} }{\mathrm {d} q}}q{\frac {\mathrm {d} }{\mathrm {d} q}}{\frac {1-q^{n+1}}{1-q}}\\&={\frac {n^{2}q^{n+3}-(2n^{2}+2n-1)q^{n+2}+(n+1)^{2}q^{n+1}-q^{2}-q}{(q-1)^{3}}}\end{aligned}}}$

For the infinite series also converge after the limit value formation of the associated finite series (consequently these can even be integrated in terms of terms): ${\displaystyle |q|<1}$

${\displaystyle \sum _{k=0}^{\infty }kq^{k}=q{\frac {\mathrm {d} }{\mathrm {d} q}}\sum _{k=0}^{\infty }q^{k}=q{\frac {\mathrm {d} }{\mathrm {d} q}}{\frac {1}{1-q}}={\frac {q}{(1-q)^{2}}}}$

${\displaystyle \sum _{k=0}^{\infty }k^{2}q^{k}=q{\frac {\mathrm {d} }{\mathrm {d} q}}q{\frac {\mathrm {d} }{\mathrm {d} q}}\sum _{k=0}^{\infty }q^{k}=q{\frac {\mathrm {d} }{\mathrm {d} q}}q{\frac {\mathrm {d} }{\mathrm {d} q}}{\frac {1}{1-q}}=q{\frac {\mathrm {d} }{\mathrm {d} q}}{\frac {q}{(1-q)^{2}}}={\frac {q(1+q)}{(1-q)^{3}}}}$

analog for higher potencies.

See also

• The convergence or divergence of the geometric series is the basis for the root criterion and the quotient criterion .
• Geometric distribution
• Arithmetic series
• Harmonic series

literature

• Albrecht Beutelspacher : Math basics at the beginning of your studies: Survival kit mathematics . Springer, 2016, pp. 198–199
• Otto Forster : Analysis 1. Differential and integral calculus of a variable. Vieweg-Verlag, 8th edition 2006, ISBN 3-528-67224-2
• George E. Andrews : The Geometric Series in Calculus . The American Mathematical Monthly, Volume 105, No. 1 (Jan., 1998), pp. 36-40 ( JSTOR 2589524 )
• Joscelyn A. Jarrett: Regular Polygons and the Geometric Series . The Mathematics Teacher, Vol. 75, No. 3 (March 1982), pp. 258-261 ( JSTOR 27962874 )

Web links

Commons : Geometric series  - collection of images, videos and audio files

Wikibooks: Math for Non-Freaks: Geometrical Series  - Learning and Teaching Materials

Wikibooks: Math for Non-Freaks: Geometric Sum Formula  - Learning and Teaching Materials

• Geometric sequences and rows on mathematische-basteleien.de
• Infinite geometric series