Limit value (sequence)
The limit or limit of a sequence of numbers is a number that the sequence comes as close as desired. This means that almost all of the sequence elements are in every neighborhood of the limit value . If a sequence has such a limit value, one speaks of convergence of the sequence - the sequence is convergent ; it converges - otherwise of divergence . An example of a convergent sequence is that as n increases, it approaches the number 0, so this is its limit value. Such a sequence is also called a zero sequence . The constant sequencealso converges, its limit value is just the number c. On the other hand, the sequence diverges , since it does not approach any number, but only alternates between the values −1 and 1 ("jumps back and forth"). The limit value of the sequence of partial sums of a series is called the limit value of the series for short; accordingly, the convergence and divergence of a series are defined.
The limit value of a sequence is not only defined for sequences of numbers, but in exactly the same way for sequences whose terms belong to a metric space , i.e. H. that a real-valued distance is defined between them . In a further generalization, a topological space is sufficient ; There the term environment , which is used here , can also be defined without metrics . See the sections Limit value of a sequence of elements of a metric space and a topological space .
Convergence is a fundamental concept in modern analysis . In a more general sense, it is dealt with in topology .
In ancient Greek philosophy and mathematics, the concept of limit values was not yet available, see for example Achilles and the turtle . The modern formulation of the concept of limit values ("for every deviation, no matter how small there is a first index ...") appeared for the first time in 1816 by Bernard Bolzano , later further formalized by Augustin-Louis Cauchy and Karl Weierstrass .
Limit of a real number sequence
Explanation and definition
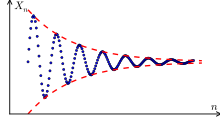
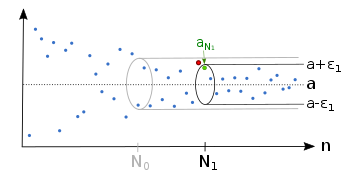
Each member of a sequence of real numbers has an index . The number is the limit value of this sequence if for each all terms with a sufficiently large index “around ” lie in the open interval . So then there are only a finite number of terms in the series outside the interval, and they all have a smaller index. The interval is the vicinity of the limit value mentioned in the introductory text; more precisely this is called the neighborhood of a and is then written. The ways of speaking " has the limit a" and " converges to a" are exactly the same.
This concretization can easily be reconciled with the clear interpretation of the convergence as “approximation to the limit value”: Regardless of how you choose that, from a certain index onwards, all terms are always in , whereby their distance is too smaller than . This gives the exact definition:
The number is called the limit of the sequence if there is a natural number for each such that , if
So this definition demands: For each there is an index with the property that all followers with the index or a larger less than from away.
This is to be understood in such a way that an arbitrarily small positive number can be given, and that it is then always possible to specify a sufficiently large one in such a way that and all subsequent terms meet the condition. One then says that almost all members of the sequence, i.e. all but a finite number of members, meet the condition.
Note 1: If the convergence of a sequence is to be demonstrated with this definition, the limit value must be known in advance. However, there are also criteria with which the convergence of a sequence can be demonstrated without the limit value being known: see convergence criteria .
Note 2: The noticeable designation “small” numbers by the letter (due to the frequency of their use) has become commonplace and is also referred to as epsilontics .
illustration
Uniqueness of the limit value
The limit value of a sequence , if it exists, is clearly defined.
This statement results directly from the definition based on a contradiction proof . If a sequence had two different limit values , they would have a distance . If one now considers environments with the two limit values, i.e. in the real case the intervals and , then these do not have a common point. According to the definition of the limit value, however, from a certain index onwards, all the elements of the sequence must lie in the environment of the limit value and thus the environments of and would have to have an infinite number of points in common. This contradiction can only be resolved if and do not have a positive distance, so the following applies.
notation
For the limit of a sequence has its own icon, you would write .
In addition to this notation, the notation for , read as converges against for against infinity , or briefly, is also common.
With this notation, the definition of the limit of a sequence can be shortened: .
Using the ambient notation, the definition is: .
Examples
The definition of the limit value should be made clear by an example, then further limit values are listed.
- In order to prove that the sequence converges against , one chooses to given as any natural number which is greater than (the existence of such a number is assured by the Archimedean axiom ). Then applies to all :
The first inequality follows from , the second from . This shows the required existence of the index , the number is the limit of the sequence .
Sequences that converge to zero, such as this example , are called zero sequences .
- The constant sequence with a fixed real number converges to .
- The consequence of the terminating decimal fraction expansions of converges against .
- The sequence with is convergent to Euler's number . The sequence converges against . This sequence of numbers occurs with the problem of constant interest (see interest calculation ).
- The sequence with is not convergent, but has two convergent subsequences for even and odd .
Calculation rules
The following calculation rules apply to limit values:
If the limit value exists , the following limit values also exist for each and can be calculated as specified:
If in addition , then the applies from a certain index and for the partial sequence
If the limit values and exist, the following limit values also exist and can be calculated as specified:
If in addition , then also from a certain index and for the partial sequence the , then applies
- .
With the help of these calculation rules, further limit values can easily be calculated from known limit values in many cases. For example, one obtains the sequence for the limit value
Limit of a bounded convergent sequence
Monotony is not a prerequisite for the consequences considered here .
- If a convergent sequence of real numbers has an upper bound (i.e. for all :) , then .
(Indirect) Proof : Assume . Then one can be given and the following applies to almost all of them (see section "Explanation and definition" above):
- (Contradiction).
- If a convergent sequence of real numbers has a lower bound (i.e. for all :) , then .
(Indirect) Proof : Assume . Then one can be given and the following applies to almost all of them (see section "Explanation and definition" above):
- (Contradiction).
Important limit values
- for complex (and thus especially for real) numbers .
- for real
- ( Euler-Mascheroni constant )
Limit value generation and function evaluation
The calculation rules can be understood as a special case of the following regularities:
- If is continuous at the point and converges to , then we have
- ;
- Is continuous at the point and converge against and against , then applies
- .
For continuous functions, limit value formation and function evaluation can be interchanged. The calculation rules given above thus follow directly from the continuity of addition, subtraction, multiplication and, if the denominator is not equal to zero, division.
In real numbers, the converse is also true: If the function is given and applies to all consequences with even so is continuous at the point .
The same applies to every function : applies to all sequences , with and also , so is continuous in the point .
Convergence criteria
In the definition of convergence given above, the limit value is used in the definition. The limit value must therefore be known or at least assumed so that the convergence of the sequence can be demonstrated with this definition. However, there are also convergence criteria with which the convergence of a sequence can be demonstrated without the limit value being known.
The monotonicity criterion states that a monotonically increasing sequence converges if and only if it is bounded above . The limit of the sequence is then less than or equal to the upper limit. Formally, the following applies:
- .
Likewise, a monotonically falling and downwardly bounded sequence converges.
The Cauchy criterion is based on the concept of the Cauchy sequence : A sequence is called a Cauchy sequence if:
- .
The Cauchy criterion now says that a sequence in the real numbers converges if and only if it is a Cauchy sequence. This criterion plays an important role in the construction of the real numbers from the rational numbers and in the extension of the concept of limit values to metric spaces .
Determination of limit values
If the convergence of a sequence has been proven, the limit value can be determined approximately in many cases by inserting a large n in the sequence and estimating the remainder. For example, for the limit value, because of the estimate, results for the estimate
However, there is no general procedure for the exact determination of limit values. In many cases, de l'Hospital's rule can be applied. Sometimes it is useful to convert the limit value into a certain integral . Often, however, only sophisticated decompositions and transformations lead to further processing.
Certain divergence
In the real numbers, a distinction is made between definite divergence and indefinite divergence:
Certain divergence against (or ) is present when a sequence x n exceeds every real number at some point and then stays above it (or falls below every real number and then remains below). This means,
or.
- .
Then you write
or.
and says that the sequence definitely diverges against or against . In this context, the values and are often called improper limit values or the specific divergence is referred to as improper convergence . The fact that these values are also viewed as limit values in a somewhat broader sense is justified insofar as the improper limit values in the extended real numbers , provided with a suitable topology, are real limit values in the sense of the general topological limit value concept described below.
Indeterminate divergence occurs when the sequence neither converges nor definitely diverges.
Examples
- The sequence of the natural numbers definitely diverges against .
- The sequence diverges indefinitely.
- The sequence diverges indefinitely.
Limit value and accumulation point
A term closely related to the limit value of a sequence is the accumulation point or also the accumulation value of a sequence. The formal definitions only differ in the position of the existential and universal quantifiers :
While the limit value as
is defined, applies to the accumulation point "only"
- is the accumulation point of .
The definition of the limit value therefore requires that in every area around the limit value, from a certain index onwards, all elements of the sequence are located; the definition of the accumulation point only requires that in every neighborhood there are infinitely many terms in series.
In the same way as the improper limit values, the improper accumulation points are occasionally defined:
- is an improper accumulation point of ,
- is improper accumulation point of .
The definition of the improper accumulation point differs from the definition of the improper limit value only in the position of the existential or universal quantifiers.
If a sequence has an actual (or improper) limit value, this limit value is also the actual (or improper) accumulation point. While a sequence has at most one limit value, it can have several accumulation points. For each actual (or improper) accumulation point there is a partial sequence which converges (or diverges in a certain way) towards this accumulation point. Conversely, if a sequence contains a convergent (or determined divergent) partial sequence, the (actual or improper) limit value of this sequence is an (actual or improper) accumulation point of the sequence.
According to the Bolzano-Weierstrass theorem , every bounded real sequence contains a convergent subsequence. If the sequence is unrestricted upwards, it contains a sub-sequence that is against a certain divergent part; if it is unrestricted downwards, it contains a against certain divergent sub-sequence. Every real sequence thus has at least one actual or improper accumulation point. The largest of these accumulation points is referred to as the limes superior, the smallest as the limes inferior. A formal definition can be found in the articles Limes superior and Limes inferior . If the limes superior and the limes inferior match, this value is also the actual or improper limit value and the result is convergent or definitely divergent. If the limes superior and the limes inferior are different, the sequence is indefinitely divergent.
Limit of a rational number sequence
The limit value of a sequence of rational numbers is formally defined like the limit value of a sequence of real numbers:
While this is not a particular restriction with and , it has a significant effect on the limit value . So there is no rational number against which the sequence given above (1, 1.4, 1.41, 1.414, 1.4142, 1.41421, ...) of the breaking decimal fraction expansions of √2 converges. The sequence is therefore divergent in the rational numbers, although it is both monotonically growing and restricted, i.e. fulfills the monotonicity criterion, and is also a Cauchy sequence, i.e. also fulfills the Cauchy criterion. The rational numbers thus have “gaps”.
These “gaps” were already known to Euclid in antiquity; However, it was not until the 19th century that these “gaps” were closed by the systematic introduction of real numbers. A frequently used way of the systematic introduction of real numbers is to first consider Cauchy sequences of rational numbers, to consider those Cauchy sequences as equivalent , the differences of which form a zero sequence, and then to define the real numbers as classes of equivalent sequences. The monotony and Cauchy criterion given above then apply in this number range extension ; in particular that every Cauchy sequence is now convergent.
In order to determine whether a sequence converges, it is therefore important to know which number range is being considered; a sequence that is convergent in the real numbers can be divergent in the rational numbers. Unless otherwise stated, limit values above the real numbers are usually considered, since these are the more suitable model for most applications.
Limit of a complex number sequence
The limit of a sequence of complex numbers is also formally defined like the limit of a sequence of real numbers:
and denote complex numbers, is still a real number. A notation of the type is no longer possible here, since no suitable order relation can be defined on the complex numbers . For the same reason, the terms monotonically rising and falling on the complex numbers cannot be appropriately defined, which is why the monotony criterion is no longer applicable. However, the second main criterion still applies: a sequence of complex numbers is convergent if and only if it is a Cauchy sequence . Another convergence criterion for complex numbers is that a sequence of complex numbers is convergent if and only if both the sequence of the real parts and the sequence of the imaginary parts converge.
Limit of a sequence of elements in a metric space
The distance between the sequence terms and the limit value was given as the amount of the difference. If the sequence members are not real numbers, but z. B. points in a three-dimensional space, the amount of the difference is replaced by a norm of the difference or, more generally, by a metric . A sequence is then defined as convergent to a limit value a , if almost all sequence members are in every ε- neighborhood of a .
Definition of convergence
Be a metric space . A sequence in is called convergent to the limit if:
In words: There is an index for any (no matter how small) (generally dependent on ) such that for all indices , all further elements of the sequence, the following applies: the distance is smaller than .
This corresponds to the definition of the convergence of a sequence of real numbers given above, it is simply replaced by .
Here too, in addition to the notation, the notation , also read as converged against , is common. If the metric meant here is not clearly identifiable, this is occasionally indicated by.
Cauchy sequences and completeness
Analogous to the real numbers, the concept of the Cauchy sequence plays an important role in metric spaces. A sequence is called a Cauchy sequence if
- .
If every Cauchy sequence has a limit, the metric space is said to be complete . In particular, the real and complex numbers are complete, but the rational numbers are not. If the metric space is not complete, it can be embedded in the complete metric space, analogous to the construction of the real numbers from the rational numbers, which is defined by the equivalence classes of Cauchy sequences with regard to the equivalence relation
is formed.
Absolute convergence
The concept of absolute convergence cannot be transferred directly to metric spaces, but there is a closely related result for complete metric spaces: a sequence is at least convergent if the sum
converges. From the convergence of this sum it follows that there exists for each one , so that for the relationship
applies. By applying the triangle inequality several times, it follows
- ,
is thus a Cauchy sequence and thus convergent in a complete space.
Limit value of a sequence of elements of a topological space
definition
The concept of limit values is generalized in the topology . If a topological space , i.e. a set with the set of subsets open in this topological space, is given, the limit value of a sequence of elements against a limit value is defined as follows:
are the so-called environments of these are the quantities for which a lot with exists.
Instead all environments to consider, it is often more convenient for the proof of convergence to a neighborhood basis to restrict, so a subset with the property that for every environment a lot to exist. The equivalent formulation that is easier to detect then applies
This concept of limit value includes the limit value of a sequence of numbers and the limit value of a sequence of elements of a metric space as special cases. In particular, in metric spaces, the set of all open spheres forms an environment basis of . If you use this environment base, you get exactly the definition of the limit value in metric spaces given above.
If a topology fulfills the first countability axiom , then limit values of sequences are sufficient to describe the topology, in particular that a point lies in the closed envelope of if and only if there is a sequence of elements that converges to. In particular, metric spaces satisfy the first countability axiom since, for example, a neighborhood basis of is.
In general topological spaces, this characterization of closed sets as limit values of sequences does not apply; there limit values of generalized sequences, so-called networks , must be considered instead of limit values of sequences .
In general topological spaces it can also be that a sequence has several limit values. For example, in the trivial topology of , in which only the empty set and even open sets are, every sequence converges to every other . But if one additionally demands that the topological space fulfills Hausdorff's axiom of separation , then in such a topological space each sequence has at most one limit value. In particular, Hausdorff's axiom of separation is fulfilled in metric spaces.
Examples
Convergence of function sequences
There are several convergence terms to describe the behavior of function sequences, as there are several distance terms in a function space and, besides the question of the existence of the limit value, questions also arise about the properties of the limit function. So the limit function of a sequence of continuous functions is not necessarily continuous.
Convergence in stochastics
In order to be able to decide appropriately, especially for applications in statistics, whether estimation or test procedures asymptotically deliver the correct results, especially for statements such as the laws of large numbers and the central limit theorems, various convergence terms have emerged in stochastics . In principle, these are also limit values of function sequences , since random variables in stochastics are modeled as functions of a probability space . For the applications of stochastics, however, it has proven to be useful to introduce your own terms and also your own terms of convergence. Examples of this are the convergence in the p-th mean , the convergence in distribution , the convergence in probability and the almost certain convergence .
Fréchet axioms
A very general concept of limit value is defined by the Fréchet axioms: A space is called a space with convergence in the sense of Fréchet, if
- Every sequence with elements of at most one limit has
- Each constant sequence to converge, and
- Each subsequence of a convergent sequence also converges and has the same limit value as the output sequence.
However, this concept of limit value does not match the concept of limit value in topology. First, sequences in topologies that do not satisfy the Hausdorff axiom can have multiple limits. Second, in topologies that do not satisfy the first countability axiom , sequences alone are not enough to uniquely describe the topology, so that the Fréchet axioms must be extended to nets . Thirdly, there are convergence terms that satisfy Frechét's axioms but cannot be generated by a topology, for example point-by-point convergence almost everywhere . In describes the additional criteria that a space with convergence in the sense of Fréchet must meet so that this convergence can be clearly generated by a topology.
General information for practice (iteration method)
Often you don't know beforehand, e.g. B. If, in an iteration process, a correction is calculated in a certain way for an input value of a variable and the value obtained in this way is taken as the new input value (i.e. in the case of a sequence ), whether this process converges. I.e. one considers an open situation in which it is neither known that a necessary criterion has been violated ( non- convergence) , nor that one of the sufficient criteria is met ( convergence). In such a case it is advisable to proceed pragmatically (ie for example with the Cauchy criterion) and simply carry out the procedure “sufficiently close” to the assumed point of convergence, although in practice it is not necessary to know what “sufficiently close” means in quantitative terms .
See also
swell
- ↑ Bernard Bolzano: The binomial theorem and as a consequence of it the polynomial, and the series that are used to calculate the logarithms and exponentials, more precisely than previously proven . Enders, Prague 1816 ( eudml.org ).
- ↑ The environment of a real number is a special case of a more general mathematical concept of the environment .
- ↑ Gabriele Adams, Hermann-Josef Kruse, Diethelm Sippel, Udo Pfeiffer: Mathematics for entry into the study. 6th edition. Springer, 2013, ISBN 978-3-642-40056-8 , p. 79.
- ^ Robert B. Ash: Real Analysis and Probability. Academic Press, New York 1972, ISBN 0-12-065201-3 , pp. 371f, Comments A.24.
- ↑ J. Cigler, H.-C. Reichel: topology. A basic lecture. Bibliographisches Institut, Mannheim 1978, ISBN 3-411-00121-6 , p. 88, exercise 6.
- ↑ John L. Kelley: General Topology. Springer Verlag, 1997, ISBN 0-387-90125-6 .























































































![\ lim _ {{n \ to \ infty}} {\ sqrt [{n}] {n}} = 1](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad8399b997df7368a350c447667a7003822626e1)




















































































