Series (math)
A series , seldom a sum sequence and especially in older representations also called an infinite series , is an object from the mathematical branch of analysis . A series is clearly a sum with an infinite number of summands . A series is precisely defined as a sequence whose terms are the partial sums of another sequence. If one counts the number 0 to the index set , the -th partial sum is the sum of the first (of the infinitely many) summands. If the sequence of these partial sums has a limit value , this is called the value or the sum of the series.
definition
If any sequence is given, a new sequence of partial sums can be formed from it . The -th partial sum is the sum of the first terms of , its definition is:
The sequence of the -th partial sums is called a series . If the series (i.e. the sequence of the partial sums) converges , its limit is called
Value of the series or sum of the series.
notation
There are different notations for rows depending on the context . This article uses the natural numbers, including zero , as indices for the terms of the sequence and series . In some applications it is advisable to only start the summation at index 1, 2 or higher; negative indices are rarely used (see Laurent series ). With the help of the sum symbol , the individual members of the series can also be abbreviated as
to be written. Proceed in the same way with the sequence of the individual members and write briefly
Often some or all of the indices are omitted to avoid misunderstandings. If, for example, in the context of calculations with infinite series, it is clear that numbering generally starts with 0, then it says
- For
Evaluation and classification
If and hence for all nonnegative indices i and n are defined thus be an infinite series form: if the limit of the sequence of partial sums
exists, it is said, the series converges; the limit S is called the sum of the series or the value of the series. This total can also be abbreviated as
to be written.
A series is called divergent or its limit value does not exist if the series does not converge. It is called definitely divergent or improperly convergent if the partial sums tend towards −∞ or + ∞. Otherwise the series is called indefinitely divergent ; it may or may not have accumulation points .
Various convergence criteria can be used to determine whether a series is converging.
Examples
A classic series is the geometric series , the name is derived from the geometric sequence ( for ). So the geometric series is:
A special geometric series is
According to the description given above, this notation denotes the limit value of the sequence
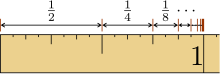
The convergence of this series can be visualized on the number line : Let us imagine a line with the length of two on which successive sections with the lengths of 1, 1/2, 1/4 etc. are marked. There is still room for one more section on this line, as there is still as much space as the last section was long: if we marked route 1/2, we have used a total of 3/2, so there is still room left 1/2 left. If we now delete 1/4, another 1/4 remains, etc. Since the “leftover piece” becomes arbitrarily small, the limit value is equal to 2.
Convergent geometric series are also a subject of Zeno's paradoxes .
An example of a divergent series with several accumulation points is the sum over the sequence +1, −1, +1, −1, ... The series changes between the values 1 and 0 (the sequence, however, changes between 1 and −1).
semantics
The symbol
have two different meanings, between which a decision must be made based on the context. The symbol stands for the value of the series, which exists in the case of convergent series or does not exist in the case of divergent series:
- .
On the other hand, the symbol represents the series as a sequence of the partial sums, regardless of the convergence behavior:
- .
The symbol almost always means the limit value. If you want to mean the sequence of the partial sums, use phrases like "... the series, viewed as the sequence of its partial sums, ..."
Calculating with series
In contrast to ordinary (finite) sums, some of the usual rules of addition only apply conditionally to series. So you can not or only under certain conditions with them as with finite sum expressions.
Sums and multiples
One can convergent series term by term, add, subtract, or by a fixed factor (but not another row) multiply (multiply). The resulting series are also convergent, and their limit value is the sum or difference of the limit values of the output series or the multiple of the limit value of the output series. I.e.
Products
One can absolutely convergent term by multiplying each series. The product line is also absolutely convergent and its limit value is the product of the limit values of the output series. I.e.
Since the notation (on the left side of the equation) of the product line with two indices is “unwieldy” in certain contexts, the product line is also written in the form of the Cauchy product . The name results from the fact that the links of the product series are formed with the help of the Cauchy diagonal method, the links of the output sequences are arranged in pairs in a square scheme, and the (numbered) diagonals of this scheme form the product links. You only need a single index for the product line. The product line then has the following form:
Calculate within the series
Brackets (associativity)
The terms within a convergent series can be grouped together using brackets. So you can insert as many brackets as you like in the "infinite sum expression", you just can't put them within a term (composed of several terms). The value of the row then does not change due to the additionally inserted brackets.
This generally does not apply to divergent series, which can easily be seen in the following example.
The series
diverges while the bracketed row
converges to zero and the series bracketed differently
converges to yet another number.
On the other hand, one can not easily clips away leave. But you can always do this when the resulting series converges again. In this case, the series value also remains unchanged. If the "less bracketed" series is convergent, you can add the same brackets to it again that you took away before, and the equality of the limit results from what has been said above if you swap the roles in it and the "less bracketed" series now as Look at the row to which brackets are added.
Rearrangement (commutativity)
A rearrangement of a series is represented by a permutation of its index set. For example, if the index set is (as is usually the case) the set of natural numbers and a bijective mapping of the natural numbers to itself, it is called
a rearrangement of the series
Convergent series can be rearranged at will while maintaining their value if and only if they are unconditionally or absolutely convergent . For unconditional (or absolutely) convergent series:
- for all bijectives .
Conditionally convergent series may only be reordered finitely, i.e. H. above a certain index must apply to the rearrangement .
Absolute and unconditional convergence
A series is called absolutely convergent if the series of its absolute terms converges.
A convergent series is formally defined as unconditionally convergent if each of its rearrangements converges again and has the same limit. The last property need not be assumed, however, since every row, the order of which is convergent, also has the same value for every order. A convergent series that is not necessarily convergent is called conditionally convergent.
In finite-dimensional spaces the following applies:
- A number is if and unconditional convergence if it is absolutely convergent.
For a conditionally convergent series, you can specify any number and then find a rearrangement of this series that converges to precisely this number ( Riemann rearrangement theorem ). In particular, you can not specify a number as a number, meaning that the series should diverge, and you will find a suitable rearrangement that does this.
Convergence criteria
In the following, the numbers are always real or complex numbers, and the series is defined as
To prove the convergence of this series there are various convergence criteria , which show partly the conditional, partly the stronger absolute convergence (convergence of the series of the amounts of the terms):
If the series converges, then the sequence ( ) of the summands for towards 0. Formulated: If ( ) is not a zero sequence , the corresponding series diverges. The converse is not generally valid (a counterexample is the harmonic series ).
If all terms of the series are nonnegative real numbers, then converges and for all
with real or complex numbers , then the series also converges
absolutely, and it is .
If all terms of the series are nonnegative real numbers, then diverges and for all
with nonnegative real numbers , then the series also diverges
- .
If a constant and an index exists, so for all true
then the series converges absolutely.
If a constant and an index exists, so for all true
then the series converges absolutely.
Is a nonnegative, monotonically decreasing function with
- for all ,
then converges if and only if the integral
exists.
A number of the form
with non-negative is called an alternating series . Such a series converges when the sequence converges monotonically to 0. The reverse is not universal.
Examples
- A geometric series converges if and only if .
- The Dirichlet series converges for and diverges for what can be shown with the integral criterion. Considered as a function of , this series gives the Riemann zeta function .
- The telescope series converges if and only if the sequence for converges against a number . The value of the range is then .
Applications
Representation of mathematical constants
In addition to the convergence and numerical value of a row, the symbolic value of a row is also important. For example, mathematical constants can be represented and calculated numerically. Example for ( natural logarithm )
- or
There are tabulations in series tables for important series representations .
Rows of functions
Instead of sequences of numbers, one can also consider sequences of functions and define rows accordingly. In addition to the question of convergence, there is also the question of the properties of the limit function. Conversely, one can ask by which row a function can be represented. Such a representation is called series development .
Power series
Some important functions can be represented as Taylor series . These are certain infinite series in which powers of an independent variable occur. Such series are generally called power series . If negative powers of the variables are also permitted, one speaks of Laurent series .
Fourier series
The Fourier series of a function is its development according to trigonometric functions and . The Euler number is also of this type.
Dirichlet series
A development is called a Dirichlet series
- With
An important example is the series representation of the Riemann zeta function
- with .
Prefix sum
In computer science, the prefix sum is an algorithm that replaces each entry in an array with the partial sum . The prefix sum can be parallelized and is therefore a basic algorithm for computer systems with several processor cores , GPUs or computer clusters .
Web links
literature
- Konrad Knopp : Theory and Application of Infinite Series . 6th edition. Springer, Berlin et al. 1996, ISBN 3-540-59111-7 , The basic teaching of the mathematical sciences in individual representations 2).
- Izrail Solomonovic Gradshteyn, Iosif Mojseevic Ryzhik: Table of Integrals, Series and Products . Edited by Alan Jeffrey and Daniel Zwillinger. 7th edition. Elsevier Academic Press, Amsterdam et al. 2007, ISBN 978-0-12-373637-6 .
Individual evidence
- ↑ Sum sequence . In: Guido Walz (Ed.): Lexicon of Mathematics . 1st edition. Spectrum Academic Publishing House, Mannheim / Heidelberg 2000, ISBN 3-8274-0439-8 .
- ↑ row . In: Guido Walz (Ed.): Lexicon of Mathematics . 1st edition. Spectrum Academic Publishing House, Mannheim / Heidelberg 2000, ISBN 3-8274-0439-8 .
- ↑ Otto Forster : Analysis Volume 1: Differential and integral calculus of a variable. Vieweg-Verlag, 8th edition 2006, ISBN 3-528-67224-2 , p. 37.
- ↑ Michelle Kuttel (2012): Parallel Java. §5 lecture slides
- ↑ Stefan Edelkamp (2010): Algorithm Engineering. Lecture slides ( Memento of the original from May 11, 2015 in the Internet Archive ) Info: The archive link was inserted automatically and has not yet been checked. Please check the original and archive link according to the instructions and then remove this notice.



























































![{\ sqrt [{n}] {| a_ {n} |}} \ leq C,](https://wikimedia.org/api/rest_v1/media/math/render/svg/61811d197fead0495fc73b8c692e7b43ed9855d3)

























