This article is about
infinite Taylor series. For the representation of functions by a partial sum of these series, the so-called Taylor polynomial, and a remainder, see
Taylor formula .

Approximation of ln (
x ) by Taylor polynomials of degrees 1, 2, 3 or 10 around the expansion point 1. The polynomials only converge in the interval (0, 2]. The radius of convergence is therefore 1.
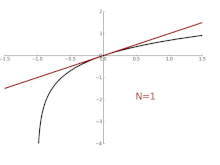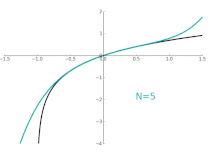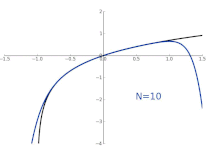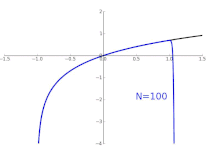
Animation for the approximation ln (1+
x ) at the point
x = 0
The Taylor series is used in analysis to represent a smooth function in the vicinity of a point by a power series , which is the limit value of the Taylor polynomials . This series expansion is called the Taylor expansion . The series and development are named after the British mathematician Brook Taylor .
definition
Be an open interval , a smooth function, and an element of . Then the infinite series is called




the Taylor series of with development point . Here refers to the faculty of and the th derivation of where you set.








Initially, the series is only to be understood “ formally ”. That is, the convergence of the series is not assumed. In fact, there are Taylor series that do not converge everywhere (for see figure above). There are also convergent Taylor series that do not converge against the function from which the Taylor series is formed (for example expanded at the point ).



In a special case , the Taylor series is also called the Maclaurin series .

The sum of the first two terms of the Taylor series

is also called linearization of at the point . In more general terms, one calls the partial sum
. In more general terms, one calls the partial sum


which represents a polynomial in the variable for fixed , the -th Taylor polynomial .



The Taylor formula with a remainder makes statements about how this polynomial deviates from the function . Due to the simplicity of the polynomial representation and the good applicability of the remainder formulas, Taylor polynomials are a frequently used aid in analysis, numerics , physics and engineering .

properties
The Taylor series for the function is a power series with the derivatives



and thus it follows by complete induction

Agreement at the development point
Because of

the Taylor series and its derivatives agree with the function and its derivatives at the point of development :




Equality with function
In the case of an analytic function , the Taylor series agrees with this power series because it holds


and thus .

Important Taylor series
Exponential functions and logarithms

Animation of the Taylor series expansion of the exponential function at the point x = 0
The natural exponential function is represented entirely by its Taylor series with expansion point 0:


With the natural logarithm , the Taylor series with expansion point 1 has the radius of convergence 1, i.e. That is, for the logarithm function is represented by its Taylor series (see figure above):


The series converges faster

and therefore it is more suitable for practical applications.
If you choose for one , then is and .




Trigonometric functions

Approximation of sin (x) by Taylor polynomials Pn of degree 1, 3, 5 and 7

Animation: The cosine function developed around the development point 0, in successive approximation
The following applies to the development point ( Maclaurin series ):


Here the -th is Bernoulli's number and the -th is Euler's number .





Product of Taylor series
The Taylor series of a product of two real functions and can be calculated if the derivatives of these functions are known at the identical expansion point :




With the help of the product rule it then results

Are the Taylor series of the two functions given explicitly?

so is

With

This corresponds to the Cauchy product formula of the two power series.
example
Be , and . Then




and we receive

in both cases

and thus

However, this Taylor expansion would also be possible directly by calculating the derivatives of :


Taylor series of non-analytical functions
The fact that the Taylor series has a positive radius of convergence at every point of expansion and that it coincides in its convergence range does not apply to every function that can be differentiated as often as desired. But also in the following cases of non-analytical functions the associated power series is called a Taylor series.


Convergence radius 0
The function

is differentiable to any number of times, but its Taylor series is in



and thus only for convergent (namely towards or equal to 1).

A function that cannot be expanded into a Taylor series at a development point
The Taylor series of a function does not always converge to the function. In the following example, the Taylor series does not match the output function on any neighborhood around the expansion point:


As a real function, it is continuously differentiable as often as required, with the derivatives in each point (especially for ) being 0 without exception. The Taylor series around the zero point is therefore the zero function and does not coincide in any neighborhood of 0 . Hence it is not analytical. The Taylor series around a point of expansion converges between and against . This function cannot be approximated with a Laurent series either, because the Laurent series which the function reproduces as correct does not result in a constant 0.











Multi-dimensional Taylor series
In the following, let us be an arbitrarily often continuously differentiable function with a development point .


Then you can introduce a family of functions parameterized with and for function evaluation, which you define as follows:





 is, as one can see by inserting , then the same .
is, as one can see by inserting , then the same .


If one now calculates the Taylor expansion at the development point and evaluates it at , one obtains the multidimensional Taylor expansion of :





With the multi-dimensional chain rule and the multi-index notations for

one also obtains:

With the notation one gets for the multidimensional Taylor series with respect to the development point


in accordance with the one-dimensional case if the multi-index notation is used.
Written out, the multidimensional Taylor series looks like this:

example
For example, according to Schwarz's theorem, for the Taylor series of a function that depends on, at the point of expansion :



![{\ displaystyle {\ begin {aligned} Tg (x; a) = & \ g (a) + g_ {x_ {1}} (a) \ cdot (x_ {1} -a_ {1}) + g_ {x_ {2}} (a) \ cdot (x_ {2} -a_ {2}) \ + \\ & + {\ frac {1} {2}} \ left [(x_ {1} -a_ {1}) ^ {2} g_ {x_ {1} x_ {1}} (a) +2 (x_ {1} -a_ {1}) (x_ {2} -a_ {2}) \, g_ {x_ {1} x_ {2}} (a) + (x_ {2} -a_ {2}) ^ {2} g_ {x_ {2} x_ {2}} (a) \ right] + \ dots \ end {aligned}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/5d496db642ca0a01d7c7abf8a6555aaa460ba5f4)
Operator form
The Taylor series can also be represented in the form
, whereby the common derivative operator is meant. The operator with is called the translation operator . If one restricts oneself to functions that can be represented globally by their Taylor series, then the following applies
. So in this case






For functions of several variables can be exchanged through the directional derivative
. It turns out



You get from left to right by first inserting the exponential series , then the gradient in Cartesian coordinates and the standard scalar product and finally the multinomial theorem .
A discrete analog can also be found for the Taylor series. The difference operator is defined by . Obviously the following applies , where the identity operator is meant. If you now exponentiate on both sides and use the binomial series , you get






One arrives at the formula

whereby the descending factorial is meant. This formula is known as the Newtonian formula for polynomial interpolation with equidistant support points. It is correct for all polynomial functions, but does not necessarily have to be correct for other functions.

See also
Web links
Individual evidence
-
^ Taylor series with a radius of convergence of zero (Wikibooks).
























































































![{\ displaystyle {\ begin {aligned} Tg (x; a) = & \ g (a) + g_ {x_ {1}} (a) \ cdot (x_ {1} -a_ {1}) + g_ {x_ {2}} (a) \ cdot (x_ {2} -a_ {2}) \ + \\ & + {\ frac {1} {2}} \ left [(x_ {1} -a_ {1}) ^ {2} g_ {x_ {1} x_ {1}} (a) +2 (x_ {1} -a_ {1}) (x_ {2} -a_ {2}) \, g_ {x_ {1} x_ {2}} (a) + (x_ {2} -a_ {2}) ^ {2} g_ {x_ {2} x_ {2}} (a) \ right] + \ dots \ end {aligned}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/5d496db642ca0a01d7c7abf8a6555aaa460ba5f4)















