Null function
In mathematics , especially in analysis , the zero function is a function whose function value is always the number zero , regardless of the value transferred . More generally, the zero mapping or the zero operator in linear algebra is a mapping between two vector spaces that always yields the zero vector of the target space . The zero mapping is grasped even more generally in algebra and there it is a mapping from any set into a set on which a link with a neutral element is defined, which always results in this neutral element. The null function has many properties and is often used as an example or counterexample in mathematics. It is the trivial solution to a number of mathematical problems , such as homogeneous linear differential equations and integral equations .
Real null function
definition
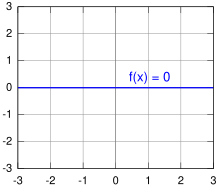
In real analysis , the null function is the real function that assigns the number zero to each argument , that is, it holds
for everyone . With the help of the identity symbol , the null function is also through
written down. The graph of the null function is the entire x-axis . Occasionally the domain of definition of the null function is restricted to a subset .
properties
classification
The null function is a special case of the following function classes:
- It is a special constant function , precisely the one whose constant is.
- It is a special linear function , namely the one whose slope and ordinate are.
- It is a special polynomial function , namely the zero polynomial , where all coefficients are. The degree of the zero polynomial is usually not defined as , but as .
Symmetries
The null function is the only function that is both even and odd at the same time , that is, it applies
- .
Further, it is neither positive nor negative , instead it is both non-positive and non-negative, that is
- and .
The zeros of the zero function are thus all numbers of the definition set and their nonzero set is therefore empty . The minimum and the maximum of the null function are also zero:
- .
Furthermore, like every constant function, the null function is monotonically increasing and decreasing at the same time (but not strictly) and, like every linear function, simultaneously convex and concave .
Derivatives
The null function is a smooth function , that is, continuously differentiable as often as desired , with each of its derivatives being the null function itself, that is
for each . Besides the exponential function , the null function is the only function with this property. The null function itself is in turn the derivative of a constant function and generally the -th derivative of a polynomial of degree .
integral
The integral of the zero function always results in zero, regardless of the integration limits
- .
for everyone . The null function is therefore the only polynomial function that can be integrated over all of the real numbers. The antiderivative of the null function is the null function itself and, since the integration constant can be freely selected, every constant function as well.
Solving equations
The null function is the trivial solution of the four Cauchy functional equations :
Furthermore, the null function solves every homogeneous linear differential equation of the form
and every homogeneous linear integral equation of the kind
with integral core and prefactor . Conversely, an inhomogeneous linear differential or integral equation is never solved by the null function.
Null mappings between vector spaces
definition
In linear algebra , a mapping between two vector spaces and over the same field is called a null mapping or null operator, if for all vectors
holds, where the uniquely determined zero vector of is. Occasionally, the zero mapping is also noted directly through , provided it is clear from the context whether the zero mapping or the number zero is meant. Here, too, the definition range of the zero mapping can be restricted to a subset .
Examples
- the real null function of the previous section and, more generally, real or complex functions of one or more variables whose function value is the number zero or the zero vector
- every mapping from any vector space into the zero vector space and every linear mapping from the zero vector space into any vector space
- a square matrix that is inserted into its characteristic polynomial , according to Cayley-Hamilton's theorem
- the determinant function on the set of singular square matrices
properties
Linearity
The zero mapping is a linear mapping , i.e. a vector space homomorphism, that is, it applies
for everyone and . So it lies in the vector space of the linear mappings and is there itself the zero vector.
Each zero mapping between finite-dimensional vector spaces is represented with respect to arbitrary bases by a zero matrix of size . Its core is whole , its image and thus its rank always . If , then the zero mapping has the number zero as its only eigenvalue and the associated eigenspace is whole .
Operator norm
If and are normalized spaces with respective norms and , then the operator norm is the zero mapping
- .
The zero mapping itself represents a semi-standard .
Solving equations
In general, the zero mapping solves any homogeneous linear operator equation
- ,
where is a linear operator, is the function you are looking for and is the null function. Conversely, an inhomogeneous linear operator equation, in which the right-hand side is not equal to the zero function, is never solved by the zero mapping.
Zero mappings into a magma with one
definition
If a set and a magma have one, that is, a set with a two-digit link with a neutral element , then a mapping is called a zero mapping if for all
applies. Important examples are monoids , groups , rings , modules and - as in the previous section - vector spaces.
Examples
- the Boolean function of contradiction in a Boolean ring or a Boolean algebra
- the polynomial function in a polynomial ring over a finite field with elements
- the -th power of a nilpotent map in a ring, if is greater than or equal to the nilpotency index of the map
- the zero dimension that assigns the value to each quantity
properties
- If and are two magmas, with one, then the zero map is a magma homomorphism .
- If and are two rings, then the null map is a ring homomorphism . If a simple ring (e.g. a solid or an oblique body ), then each ring homomorphism is either injective or the null map.
- If and are two modules, then the null map is a module homomorphism .
- If and are two algebras over a ring , then the zero mapping is an algebra homomorphism .
See also
literature
- Martin Barner, Friedrich Flohr: Analysis I . de Gruyter, 2000, ISBN 3-11-016778-6 .
- Siegfried Bosch : Linear Algebra . Springer, 2009, ISBN 3-540-76437-2 .
- Christian Karpfinger, Kurt Meyberg: Algebra: Groups - Rings - Body . Springer, 2008, ISBN 3-8274-2018-0 .
- Gilbert Strang : Linear Algebra . Springer, 2003, ISBN 3-540-43949-8 .
Individual evidence
- ↑ Barner, Flohr: Analysis I . S. 247 .
- ^ Bosch: Linear Algebra . S. 78 .
- ^ Bosch: Linear Algebra . S. 204 .
- ^ Bosch: Linear Algebra . S. 141 .
- ^ Bosch: Linear Algebra . S. 93 .
- ↑ Karpfinger, Meyberg: Algebra: Groups - Rings - Body . S. 158 .
- ↑ Karpfinger, Meyberg: Algebra: Groups - Rings - Body . S. 181 .
- ↑ Karpfinger, Meyberg: Algebra: Groups - Rings - Body . S. 172 .
Web links
- Eric W. Weisstein : Zero Map . In: MathWorld (English).
- matte, yark: Zero Map . In: PlanetMath . (English)