Convex and concave functions
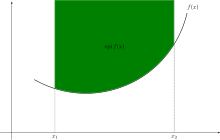
In analysis , a real-valued function is called convex if its graph lies below every connecting line between two of its points. This is equivalent to the fact that the epigraph of the function, i.e. the set of points above the graph, is a convex set .
A real-valued function is called concave if its graph lies above each line connecting two of its points. This is synonymous with the fact that the hypograph of the function, i.e. the set of points below the graph, is a convex set.
One of the first to study the properties of convex and concave functions was the Danish mathematician Johan Ludwig Jensen . Jensen's inequality named after him is the basis of important results in probability theory , measurement theory and analysis.
The special importance of convex or concave functions is that they form a much larger group than the linear functions , but also have many properties that are easy to investigate and that enable statements about non-linear systems . For example, since every local minimum of a convex function is also a global minimum, they are important for many optimization problems ( see also: Convex Optimization ). Even for convex functionals that are defined on infinitely dimensional spaces, similar statements can be made under certain conditions. Therefore, convexity also plays an important role in the calculus of variations .
definition

There are two equivalent definitions, on the one hand one can define convexity using an inequality over the function values (analytical definition), on the other hand using the convexity of sets (geometric definition).
Analytical definition
A function where is a convex subset is called convex if for all out and for all that
Geometric definition
A function is called convex if its epigraph is a convex set . This definition has certain advantages for extended real functions which the values can also assume and for which the undefined term can occur with the analytical definition . The convexity of the epigraph also shows that the definition set is a convex set. A convex function always has a convex definition set; conversely, a function is not convex if its definition set is not convex.
Concave functions
If it is a convex function, it is called concave . For concave functions the definitions are reversed, so the analytical definition of a concave function is
the geometrical definition of a concave function requires that the hypograph be a convex set.
Further classifications
A function is called strictly convex or strictly convex if the inequality of the analytic definition holds in the strict sense; that is, for all elements from , and all rule,
- .
A function is called strongly convex with parameter or -convex , if for all and it holds that
- .
Strongly convex functions are also strictly convex, but the converse is not true.
There is also the concept of the uniformly convex function, which generalizes the concept of strong convexity. A function is called uniformly convex with modulus , where is increasing and only disappears at 0 if for all and the following applies:
- .
If you choose with , you get the inequality for strong convexity.
For the terms strictly convex, strongly convex and uniformly convex, the corresponding counterparts can be defined strictly concave, strongly concave and uniformly concave by reversing the respective inequalities.
Examples
- Linear functions are entirely convex and concave, but not strictly.
- The quadratic function is strictly convex.
- The function is strictly convex.
- The function is not convex because the definition set is not a convex set.
- The function is strictly concave.
- The root function is strictly concave in the interval .
- The absolute value function is convex, but not strictly convex.
- The exponential function is strictly convex on whole .
- The natural logarithm is strictly concave on the interval of positive real numbers.
- The cubic function is strictly concave on the interval and strictly convex on the interval .
- The function that maps a point on the Euclidean plane to its distance from the origin, i.e.
- is an example of a convex function on a multidimensional real vector space.
history
Essential statements on convex and concave functions can be found in Otto Hölder's work as early as 1889 , although he did not yet use the terms commonly used today. The terms convex and concave function were introduced by Johan Ludwig Jensen in 1905 . Jensen, however, used a weaker definition that can still be found occasionally, especially in older works. In this definition only the inequality
provided. As Jensen showed, however, the inequality used in today's definition for continuous functions follows from this
for all between 0 and 1. ( see also: section convexity and continuity )
Real-valued functions that satisfy the weaker inequality ( ) mentioned above are called Jensen-convex or J-convex for short , in honor of Johan Ludwig Jensen .
Elementary properties
Convex and concave ratio
The function is (strictly) convex if and only if the function is (strictly) concave. However, a non-convex function does not necessarily have to be concave. Convexity and concavity are therefore not complementary properties .
Linear functions are the only functions that are both concave and convex.
- example
The cubic function is in a very considered concave not convex yet. The interval of all positive real numbers is strictly convex. The function that is additively inverse to it is therefore strictly concave there.
Since is an odd function , that is, it follows that it is strictly concave in the range of all negative numbers.
Level quantities
In the case of a convex function, all sub-level sets, i.e. sets, are of the form
convex. In the case of a concave function, all suplevel sets are convex.
Jensen's inequality
The Jensen's inequality is a generalization of the analytic definition to a finite number of nodes. It states that the function value of a convex function at a finite convex combination of support points is less than or equal to the convex combination of the function values at the support points. For a convex function and for nonnegative ones with :
For concave functions, the inequality applies in the opposite direction.
Reduction to convexity of real functions
The archetype space of a convex function can be any real vector space, such as the vector space of the real matrices or the continuous functions. However, the convexity of a function is equivalent to the convexity of the function defined by for all , where is and any direction is off. It is then . This makes it possible to reduce the dimension of the vector space, which makes it easier to check the convexity.
Inequalities for and
For or , the inequalities from the definitions of (strict) convexity and concavity are reversed. For example, be a function that is convex. For points and from then applies
provided that the point is also within the definition range. If is a real convex function, the inequality clearly means that the function values from outside the interval are always above the straight line connecting the function values .
Calculation rules
Positive combinations
The sum of two (possibly extended ) convex functions is again a convex function. In addition, convexity is preserved when multiplying by a positive real number. In summary, it is true that every positive combination of convex functions is convex in turn. It is even strictly convex if one of the summands occurring is strictly convex. Similarly, every positive combination of concave functions is also concave. Thus the convex functions form a convex cone . However, the product of convex functions is not necessarily convex.
- example
The functions
are convex all over , the norm parabola is even strictly convex. It follows that all functions of form
with strictly convex on whole . This is also vividly clear, these are upwardly curved parabolas. The product of the functions and is the cubic function , which ( considered over all ) is not convex.
Limit functions
The limit function of a point-wise convergent sequence of convex functions is a convex function. Likewise, the limit function of a point-wise convergent series of convex functions is again a convex function. The same clearly applies to concave functions. However, strict convexity is not necessarily retained under the limit value formation, as can be seen from the first of the two following examples.
- Examples
- The sequence of functions with is a sequence of strictly convex functions. Its point-wise limit function is the constant zero function . As a linear function, this is convex, but not strictly convex.
- The hyperbolic cosine can be expanded as a power series as follows :
- All summands that occur are convex functions. It follows from this that the hyperbolic cosine is also a convex function.
Supremum and Infimum
Is a set of convex functions and the supremum exists point by point
for all so is also a convex function. The transition to the function shows that the infimum of a set of concave functions (if it exists) is also a concave function again. However, the formation of the infimum does not necessarily acquire convexity (and conversely, the formation of the supremum does not necessarily acquire concavity), as the following example shows.
- example
The real functions
are linear and therefore both convex and concave. The supremum of and is the amount function . This is convex, but not concave. The infimum of and is the negative amount function . This is concave, but not convex.
composition
About the composition of two convex functions and no statement can meet in general. However , if it is also true that there is a monotonous increase , then the composition is also convex.
Furthermore, the composition of a concave function with a convex, monotonically decreasing real function is in turn a convex function.
- example
Every composition of a convex function with the exponential function provides a convex function. This also works in the general case in which a real vector space is defined. For example, for
again a convex function. In particular, every logarithmically convex function is a convex function.
Inverse functions
If an invertible and convex function is defined on an interval, then it follows from the convexity inequality
Let be a monotonically increasing function . Then the above inequality is reversed when applying . The following applies:
So the inverse function is a concave (and monotonically increasing) function. For an invertible, monotonically increasing and convex or concave function, the inverse function therefore has the opposite type of convexity.
For a monotonically falling and convex function , however, the following applies
For an invertible monotonically falling and convex or concave function, the inverse function therefore has the same type of convexity.
- Examples
- The norm parabola is monotonically increasing and strictly convex . Its inverse function, the root function, is strictly concave on its definition interval
- The function is monotonically decreasing and strictly convex over the whole . Its inverse function is strictly convex on the interval
Extreme values
If the starting space of a convex / concave function is a topological vector space (which applies in particular to all finite-dimensional real vector spaces and thus also to ), statements can be made about the relationship between local and global extreme points. It then applies that every local extreme point is also a global extreme point. Strict convexity or concavity also allows statements about the uniqueness of extreme values .
Existence and uniqueness
A continuous convex or concave function takes a minimum and a maximum on the compact set . The compactness of is equivalent to being bounded and closed. This is the theorem of minimum and maximum applied to convex and concave functions. If the function is strictly convex, the minimum is clearly determined, if it is strictly concave, the maximum is clearly determined. However, the reverse is not true: the function has no global minimum in , but is strictly convex.
There are analogous statements for a continuous function on a reflexive Banach space : A continuous convex functional on the compact set assumes a minimum there. If the functional is strictly convex, the minimum is unique.
Geometry of the optimal value sets
In topological vector spaces (which are almost always given) one can also investigate local minima. The following applies:
- If the function is convex, then every local minimum is also a global minimum.
- If the function is concave, then every local maximum is also a global maximum.
This can be shown directly with the defining inequalities of convex and concave functions.
In addition, the set of minimum points of a convex function is convex and the set of maximum points of a concave function is convex. This follows from the convexity of the sub-level quantities or super-level quantities.
Criteria for extreme values
For differentiable convex functions, to determine the extreme values, use is made of the fact that convex functions are globally underestimated at every point by the tangent at this point. It applies , where denotes the standard scalar product. If the gradient is now zero at one point , then for all and thus is a local (and thus global) minimum. Analogously, with concave functions there is always a local (and thus global) maximum at a point if the gradient or the derivative at this point disappears.
Convexity and continuity
If one assumes the continuity of a real function , the condition that the following inequality holds for all of the definition interval is sufficient to show its convexity :
This corresponds to Jensen's definition of convexity. Conversely, every function defined on an interval that satisfies the above inequality is continuous at the inner points . Discontinuities can occur at most in edge points, like the example of the function with
shows, which is convex, but has a discontinuity at the edge point .
Thus, the two ways of defining convexity are equivalent, at least for open intervals. To what extent this result can be transferred to general topological spaces is dealt with in the following two sections.
In this context the Bernstein-Doetsch theorem should be mentioned, from which the following result can generally be obtained:
-
If des is a real-valued function for a convex open subset , then it is both Jensen-convex and continuous if and only if for every two points and every real number the inequality is always
- is satisfied.
A weaker definition of convexity
A continuous function on a convex subset of a real topological vector space is convex if there is a fixed one with , so that for all , from :
This can be shown by means of suitable interval nesting. A fully executed evidence is in the evidence archive .
That continuity is required in this weaker definition of convexity can be seen from the following counterexample.
- Counterexample
Let be a Hamel basis of the vector space of the real numbers over the field of the rational numbers, i.e. a set of real numbers linearly independent over the rational numbers, in which every real number has a unique representation of the kind with only finitely many rational ones. Fulfilled for any choice of the function while but not necessarily convex.
Limitation and continuity in standardized spaces
If one sets for a function in addition to the condition that for a fixed the relationship
for all , from a convex subset of a normalized vector space , it still holds in advance that it is bounded upwards , then this already implies the continuity of in the inner points of . This becomes clear from the fact that at a point of discontinuity one can draw any steep connecting line between two function values, whereby the function between the two values must lie below the connecting line and outside the two values above the connecting line. If the straight connecting line can now become as steep as you want, at some point you will come across the upper limit of the function.
Formally, however, the proof is somewhat more complicated. A complete version is in the evidence archive .
The statement that a convex bounded function is continuous at the inner points is also significant for solving Cauchy's functional equation
From this statement it follows that this functional equation has a unique solution if it is additionally required that it is bounded.
In finite-dimensional spaces
Convex functions , which are defined on a subset of a finite-dimensional real vector space , are continuous in the interior points. To see this, consider an internal point . For this there is a simplex with the corner points , which again contains as an inner point. But every point is in the form
- With
and representable for everyone . According to those inequality, the following applies
- .
is therefore bounded upwards to and thus, as shown above, continuous at the inner point .
In infinitely dimensional spaces
In the infinite-dimensional case, convex functions are not necessarily continuous, since there are in particular linear (and thus also convex) functionals that are not continuous.
Convexity and differentiability
Convexity and first derivative
A convex or concave function defined on an open interval is locally Lipschitz continuous and thus, according to Rademacher's theorem, differentiable almost everywhere . It can be differentiated in every point on the left and right .
Derivation as a convexity criterion
The first derivative can be used as a convexity criterion in two ways. Is a continuously differentiable real function
- then becomes convex if and only if its derivative increases monotonically there .
- strictly convex if and only if its derivative grows strictly monotonically there .
- concave if and only if its derivative there is monotonically decreasing.
- strictly concave if and only if its derivative there is strictly monotonically decreasing.
This result can essentially be found as early as 1889 with Otto Hölder . With the extended monotony term for vector-valued functions , this can also be extended for functions . Then (strictly / uniformly) is convex if and only if (strictly / uniformly) is monotonic.
Alternatively, is a differentiable function if and only
- convex if is for everyone .
- strictly convex if is for everyone .
- concave when is for everyone .
- strictly concave when is for everyone .
In the case of a function, it simplifies to .
example
Consider the logarithm as an example . It is continuously differentiable on the interval with derivative .
After the first convexity criterion, the derivation must now be examined for monotony. Is and , so is , since the numerator and denominator are really positive. Thus is strictly monotonically falling and consequently is strictly concave on .
After the second criterion of monotony, one checks for
- .
But since for is, the inequality holds if is and are. So the logarithm is strictly concave on .
Looking at the function
- ,
so all partial derivatives are continuous and holds for the gradient
To check the first convexity criterion, one forms for
- ,
since the quadratic terms are always really positive, the positivity of the terms follows from the monotony of the exponential function. The function is therefore strictly monotonic, i.e. also strictly convex.
Tangents
The graphs of differentiable convex functions lie above each of their tangents . Similarly, concave functions are always below their tangents. This follows directly from the second convexity criterion. This can also be interpreted in such a way that the Taylor expansion of the first degree always globally underestimates a convex function. From these properties, for example, the generalization of the Bernoulli inequality follows:
- for or
- for .
Convexity and second derivative
Convexity criteria and two-fold differentiability
Further statements can be made for a function that can be differentiated twice . is convex if and only if its second derivative is not negative. Is consistently positive, i.e. always curved to the left , then it follows that it is strictly convex. Analogous to this is concave if and only if applies. If it is consistently negative, i.e. always curved to the right, it is strictly concave.
Is the multidimensional function twice continuously differentiable , then applies that then is convex accurate when the Hessian matrix of positive semidefinite is. If the Hessian matrix is positive , then it is strictly convex. Conversely, it is concave if and only if the Hessian matrix is negative semidefinite . If the Hessian matrix is negative , then it is strictly concave.
In essence, the second-order convexity criteria are based on checking the monotony of the derivation using monotony criteria, which in turn are based on differentiability.
Examples
The function with is convex because it applies to everyone . In fact, it is strictly convex, which proves that strict convexity does not imply that the second derivative is positive ( has a zero at 0).
The function considered above is twice continuously differentiable with a second derivative for all . So the function is strictly concave.
Looking at the function
- ,
so is her Hessian matrix
- .
It is positive definite because all of its intrinsic values are genuinely positive. So it is strictly convex.
Convex functions in geometry
A non-empty, closed subset of a real normalized vector space is convex if and only if the through
defined distance function is a convex function .
The same property applies not only to subsets of , but also in general to subsets of CAT (0) spaces , in particular of Riemannian manifolds of non-positive section curvature . The convexity of the distance function is an important tool when studying non-positively curved spaces.
Generalizations
For real-valued functions
- A quasi-convex function generalizes the property of a convex function that its sub-level sets, i.e. sets of form
- ,
- are convex. A function is quasi-convex if each sub-level set is convex. Every convex function is quasi-convex, the reverse is not true.
- A pseudoconvex function is a differentiable function , for which applies: If applies, then it follows . These functions generalize the property of convex functions that there is a global minimum at a point with a vanishing gradient. Every differentiable convex function is pseudoconvex.
- Logarithmic convexity of a function occurs when is convex. Strictly speaking, logarithmically convex functions are not a generalization, but a special case of convex functions.
For functions in finite-dimensional vector spaces
- K-convex functions generalize convexity of functions that map to the case that the function maps to, i.e. is vector-valued. This is done using generalized inequalities .
- A special case of K-convex functions are the matrix-convex functions . They map into the space of real symmetrical matrices, provided with the Loewner partial order .
For mapping in general real vector spaces
- The almost convex functions generalize the convexity in such a way that the best possible regularity requirements apply to them in the optimization.
- A convex map is a map between two real vector spaces for which
- holds for all and from the convex set . Here is a positive cone on .
In relation to reference systems
- Generalized convexity defines the convexity of a function in relation to a set of maps, the so-called reference system.
Individual evidence
- ^ Ralph Tyrell Rockafellar: Convex Analysis . Princeton University Press, Princeton 1970, ISBN 978-1-4008-7317-3 , Section 4.
- ^ Heinz H. Bauschke, Patrick L. Combettes: Convex Analysis and Monotone Operator Theory in Hilbert Spaces . In: CMS Books in Mathematics . 2011, ISSN 1613-5237 , doi : 10.1007 / 978-1-4419-9467-7 .
- ↑ a b Otto Hölder : About a mean value proposition . In: News from the Royal. Society of Sciences and the Georg August University in Göttingen . From 1889., No. 1-21 . Dieterichsche Verlag-Buchhandlung, Göttingen 1889, p. 38 ff . (in Wikisource [accessed March 24, 2012]).
- ↑ Earliest Known Uses of Some of the Words of Mathematics, July 28, 2006 : A. Guerraggio and E. Molho write, “The first modern formalization of the concept of convex function appears in JLWV Jensen Om konvexefunktioner og uligheder mellem midelvaerdier, Nyt Tidsskr. Math. B 16 (1905), pp 49-69. Since then, at first referring to Jensen's convex functions, then more openly, without needing any explicit reference, the definition of convex function becomes a standard element in calculus handbooks. ”(“ The Origins of Quasi-concavity: a Development between Mathematics and Economics ", Historia Mathematica, 31, (2004), 62-75.)
- ↑ z. B. in IP Natanson: Theory of the functions of a real variable , 4th edition, Verlag Harri Deutsch, Thun, 1981, ISBN 3-87144-217-8 .
- ↑ Jensen, JLWV: Sur les fonctions convexes et les inégalités entre les valeurs moyennes. In Acta Math. 30, 175-193, 1906.
- ^ Marek Kuczma: An Introduction to the Theory of Functional Equations and Inequalities. 2009, p. 130 (footnote)
- ↑ Kuczma. op. cit., pp. 161-162
- ↑ Ballmann, Werner; Gromov, Mikhael; Schroeder, Viktor: Manifolds of nonpositive curvature. Progress in Mathematics, 61. Birkhauser Boston, Inc., Boston, MA, 1985. ISBN 0-8176-3181-X
Web links
literature
- Stephen Boyd, Lieven Vandenberghe: Convex Optimization . Cambridge University Press, Cambridge, New York, Melbourne 2004, ISBN 978-0-521-83378-3 ( online ).
- Peter Kosmol: Optimization and Approximation (= De Gruyter Studies ). 2nd Edition. Walter de Gruyter & Co. , Berlin 2010, ISBN 978-3-11-021814-5 ( MR2599674 ).
- Marek Kuczma : An Introduction to the Theory of Functional Equations and Inequalities . Cauchy's Equation and Jensen's Inequality. 2nd Edition. Birkhäuser Verlag , Basel 2009, ISBN 978-3-7643-8748-8 ( MR2467621 ).
- Kurt Leichtweiß : Convex quantities (= university text ). Springer-Verlag, Berlin, Heidelberg, New York 1980, ISBN 3-540-09071-1 ( MR0586235 ).
- Jürg T. Marti: Convex Analysis (= textbooks and monographs from the field of exact sciences, mathematical series . Volume 54 ). Birkhäuser Verlag , Basel, Stuttgart 1977, ISBN 3-7643-0839-7 ( MR0511737 ).









![{\ displaystyle \ theta \ in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fead1e7dceab4be5ab2e91f5108144722daa8c36)






![{\ displaystyle \ forall x, y \ in C, \ \ theta \ in [0,1]: \ quad f (\ theta x + (1- \ theta) y) \ geq \ theta f (x) + (1- \ theta) f (y),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/93e60e526141dc5f2ef785c2f802dfb5ce355182)







![{\ displaystyle \ phi: \ mathbb {R} _ {+} \ to [0, \ infty]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eb27adbdd25d8886f0de56260f38d10e38b1a2af)























































































![t \ in [0.1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/31a5c18739ff04858eecc8fec2f53912c348e0e5)










































































![\ lambda \ in [0,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/010c0ee88963a09590dd07393d288edd83786b91)


