Function graph

Graph of the function ${\displaystyle f(x)=x^{3}-9x}$

Graph of the function ${\displaystyle f(x,y)=\sin \left(x^{2}\right)\cos \left(y^{2}\right)}$

As a function graph or short Graph (rare: function Count or Count ) of a function is called in mathematics the set of all ordered pairs of the elements of the definition set and the corresponding function values . ${\displaystyle f}$ ${\displaystyle (x,f(x))}$ ${\displaystyle x}$ ${\displaystyle f(x)}$

Sometimes these pairs can be interpreted as points in the plane of the drawing or in the visual space, they are also called curve , curve progression or also function graph .

definition

The graph of a function with a definition set and a target set is the set ${\displaystyle f\colon D\to Z}$ ${\displaystyle D}$ ${\displaystyle Z}$

${\displaystyle G_{f}=\{(x,f(x))\in D\times Z\mid x\in D\}}$.

The graph is thus a special subset of the Cartesian product of the definition and target set. It consists of all pairs in which the first component is an element of the definition set and the second component is the element of the target set assigned to this element by the function.

Special cases and examples

The graph of a function with is a subset of and can thus be understood as a point set or a geometric figure in the plane . Examples are: ${\displaystyle f\colon D\to \mathbb {R} }$ ${\displaystyle D\subseteq \mathbb {R} }$ ${\displaystyle \mathbb {R} \times \mathbb {R} =\mathbb {R} ^{2}}$

• The graph of a linear function is a straight line . ${\displaystyle f\colon \mathbb {R} \to \mathbb {R} ,x\mapsto ax+b}$
• The graph of a quadratic function with is a parabola . ${\displaystyle f\colon \mathbb {R} \to \mathbb {R} ,x\mapsto ax^{2}+bx+c}$ ${\displaystyle a\neq 0}$
• The graph of the reciprocal function is a hyperbola . ${\displaystyle f\colon \mathbb {R} \setminus \{0\}\to \mathbb {R} ,x\mapsto {\tfrac {1}{x}}}$

The graphs of functions or are subsets of and can also be represented graphically as spatial figures. Examples are: ${\displaystyle f\colon \mathbb {R} ^{2}\to \mathbb {R} }$ ${\displaystyle f\colon \mathbb {R} \to \mathbb {R} ^{2}}$ ${\displaystyle \mathbb {R} ^{3}}$

• The graph of a continuous function is a surface in three-dimensional space. For example, the graph of the function is an elliptical paraboloid . ${\displaystyle f\colon \mathbb {R} ^{2}\to \mathbb {R} }$ ${\displaystyle f(x,y)=x^{2}+y^{2}}$
• The graph of a continuous function is a curve in three-dimensional space. For example, the graph of the function is a helix . ${\displaystyle f\colon \mathbb {R} \to \mathbb {R} ^{2}}$ ${\displaystyle f(t)=(\sin t,\cos t)}$

Use in math

In set- theoretical definitions of functions, these are often defined as a set of digit-value pairs, that is, the graph would be nothing other than the function itself, that is . Jean Dieudonné pointed out this curiosity as early as 1960 : ${\displaystyle G_{f}=\{(x,f(x))\in D\times Z\mid x\in D\}=f}$

It is customary, in the language, to talk of a mapping and a functional graph as if they were two kinds of objects in one-to-one correspondence, and to speak therefore of "the graph of a mapping", but this is a mere psychological distinction (corresponding to whether one looks on F either “geometrically” or “analytically”).

In the case of mathematical considerations that are not directly in the context of the set-theoretical foundation of the mathematical terms, one does not usually assume a set structure of a function, but only demands the definition of the image at a given point. Set operations are then not carried out on functions (for example, this would usually not be regarded as a meaningful expression), but in some cases it is practical to consider a function as a set with the operations and properties defined on sets; this consideration is done via the graph of the function. In addition to the possibility of viewing a function as a geometric figure, further examples are given here: ${\displaystyle \sin \cap \cos }$

• In every Polish space a function is Borel measurable if and only if the graph is a Borel set .
• Theorem of the closed graph : A linear operator between Banach spaces is continuous if and only if its graph is closed.

Graph in the sense of graphic representation

The graph is not a mathematical object . It serves as an illustration in the context of mathematics and allows speculations about the properties of a function.

Graphs of discontinuous functions, definition gaps

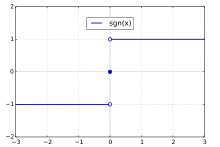
In the representation of the graphs of discontinuous functions or of functions with definition gaps , it is often indicated by that a point belongs to the graph and by that a point is not part of the graph. One example is the illustration of the sign function (also known as the “ sign function”). ${\displaystyle \bullet }$ ${\displaystyle \circ }$

Examples

Three examples of function graphs:

function	graph	annotation
${\displaystyle f(x)={\begin{cases}-1&{\mbox{falls }}x<0\\0&{\mbox{falls }}x=0\\1&{\mbox{falls }}x>0\end{cases}}}$		The function value of the sign function at position 0 is 0.
${\displaystyle f(x)={\begin{cases}0&{\mbox{falls }}x=1\\8&{\mbox{falls }}x=2\\15&{\mbox{falls }}x=3\end{cases}}}$		Since the domain is the set , the graph consists only of the three points , and . ${\displaystyle \{1,2,3\}}$ ${\displaystyle (1,0)}$ ${\displaystyle (2,8)}$ ${\displaystyle (3,15)}$
${\displaystyle f(x)={\frac {1}{x}}}$		The reciprocal function is not defined for. Therefore there is no point on the function graph with the coordinate 0. ${\displaystyle x=0}$ ${\displaystyle x}$

Individual evidence

1. ↑ Schichl & Steinbauer 2012, p. 160.
2. ↑ Dieudonné 1960, p. 5; Hischer 2016, p. 146, p. 237
3. ^ JJ Buckley, Graphs of Measurable Functions (PDF; 304 kB) , Proceedings of the American Mathematical Society , Volume 44, Number 1, May 1974

literature

• Dieudonné, Jean Alexandre: Foundations of Modern Mathematics . New York / London: Academic Press 1960.
• Hischer, Horst: Mathematics - Media - Education . Wiesbaden: Springer Spectrum 2016, ISBN 978-3-658-14166-0 .
• Hermann Schichl , Roland Steinbauer: Introduction to mathematical work. Berlin / Heidelberg: Springer 2012, 2nd edition, ISBN 978-3-642-28645-2 .

Web links

• Eric W. Weisstein : Function Graph . In: MathWorld (English).