Continuous function

In mathematics , a continuous mapping or continuous function is a function in which sufficiently small changes in the argument result in only arbitrarily small changes in the function value. This property can be formalized with the interchangeability of the function with limit values ​​or with the - criterion. ${\displaystyle \varepsilon }$ ${\displaystyle \delta }$

Clearly speaking, a real continuous function is characterized by the fact that its graph is a coherent curve in a Cartesian coordinate system within its definition range, i.e. the graph does not make any jumps and can be drawn without removing the pen. ${\displaystyle y=f(x)}$

Many functions used in the practice of real analysis are continuous; this is particularly the case for all differentiable functions.

A number of useful properties can be proven for continuous functions. The interim value theorem , the theorem of minimum and maximum and the fundamental theorem of analysis are mentioned as examples .

More generally, the concept of the continuity of mappings is of central importance in mathematics, especially in the sub-areas of analysis and topology . It is possible to characterize continuity by a condition that only uses terms from topology. Thus the concept of continuity can also be extended to functions between topological spaces . From a mathematical point of view, this general view turns out to be the “most natural” approach to the concept of continuity: Continuous functions are those functions between topological spaces that are “compatible” with their structures. Continuous functions play a similar role in topology and analysis to homomorphisms in algebra .

motivation

Graphical illustration of the function with a jump point in . ${\displaystyle f}$ ${\displaystyle x=1}$

The function

${\displaystyle f(x)={\begin{cases}x,&{\text{wenn }}x\leq 1\\x+1,&{\text{wenn }}x>1\end{cases}}}$

“Jumps” at the point from function value 1 to function value 2. If the function represents a relationship from nature or technology, such behavior appears to be unexpected ( natura non facit saltus ). For example, if the function describes the relationship between the energy applied while cycling and the speed achieved, it would be surprising if a minimal increase in the applied energy at one point suddenly led to the speed doubling. ${\displaystyle x=1}$

The mathematical concept of continuity tries to describe exactly those functions that do not have such an “arbitrary” behavior. The given function is not continuous, whereby the discontinuity can be restricted to the point . In all other points the function is continuous. ${\displaystyle f}$ ${\displaystyle x=1}$

Sine and cosine are continuous functions, their function graphs can be drawn in one go without stopping.

Consistency is often associated with being able to draw the graph of a function in one go without stopping. This view comes up against certain limits, especially when one considers functions with other domains of definition than the entire real number line. Therefore, mathematically exact definitions are required.

The graph of the continuous function in two different scales. ${\displaystyle x\sin(1/x)}$

For example, it's through

${\displaystyle g(x)={\begin{cases}x\cdot \sin {\frac {1}{x}},&{\text{wenn }}x\not =0\\0,&{\text{wenn }}x=0\end{cases}}}$

The given function is clearly continuous, because apart from at its graph is a continuous line, and at it has no place to make "jumps". Whether or not it can be drawn “without offset” down to the zero point cannot be decided without a more precise definition of what a permitted drawing should be. It is easier to develop a definition of “continuous” without the term “draw”, according to which this function can be proven to be continuous. Then the reasons just mentioned can certainly contribute to the proof. ${\displaystyle x=0}$ ${\displaystyle x=0}$

Detailed investigation of the behavior from close up : drawing possible? ${\displaystyle g(x)}$ ${\displaystyle x=0}$

---

The function is straight , so that it suffices to limit the investigation to its behavior for . In addition to the zero at the zero point, their positive zeros are at the positions for integer ; these are indexed from right to left, i.e. H. with as the largest zero and with an infinite number of additional zeros between and any other zero . Between the neighboring zeros and there is a position with , so that . Between the zeros and so the graph has to overcome the height difference twice , so that its length in this section is more than . Between the zero and any other positive zero further to the left, the length of the graph is therefore greater than . This sum increases with increasing over all limits (see harmonic series ), so that the complete drawing would never be finished. ${\displaystyle g}$ ${\displaystyle x\geqq 0}$ ${\displaystyle x_{k}={\tfrac {1}{k\pi }}}$ ${\displaystyle k>0}$ ${\displaystyle x_{1}>x_{2}>\dotsb >0}$ ${\displaystyle x_{1}}$ ${\displaystyle 0}$ ${\displaystyle x_{k}}$ ${\displaystyle x_{k}}$ ${\displaystyle x_{k-1}}$ ${\displaystyle \xi _{k}={\tfrac {2}{(2k-1)\cdot \pi }}}$ ${\displaystyle \sin {\tfrac {1}{\xi _{k}}}=\pm 1}$ ${\displaystyle |g(\xi _{k})|=\xi _{k}={\tfrac {2}{(2k-1)\cdot \pi }}>{\tfrac {1}{k\pi }}}$ ${\displaystyle x_{k}}$ ${\displaystyle x_{k-1}}$ ${\displaystyle {\tfrac {1}{k\pi }}}$ ${\displaystyle {\tfrac {2}{k\pi }}}$ ${\displaystyle x_{1}}$ ${\displaystyle x_{n}}$ ${\displaystyle {\tfrac {2}{\pi }}\cdot ({\tfrac {1}{1}}+{\tfrac {1}{2}}+\dotsb +{\tfrac {1}{n-1}})}$ ${\displaystyle n}$

Continuity of real functions

definition

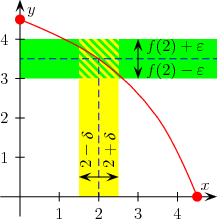
Let be a real function , i.e. a function whose function values ​​are real numbers and whose domain also consists of real numbers. In real analysis there are several equivalent ways of defining the continuity of in one . The most common are the epsilon delta criterion and the definition using limit values. ${\displaystyle f}$ ${\displaystyle f\colon D_{f}\to \mathbb {R} }$ ${\displaystyle D_{f}\subset \mathbb {R} }$
${\displaystyle f}$ ${\displaystyle {\displaystyle x_{0}\in D_{f}}}$

Illustration of the - definition: for satisfies the continuity condition. ${\displaystyle \varepsilon }$ ${\displaystyle \delta }$ ${\displaystyle \varepsilon =0.5}$ ${\displaystyle \delta =0.5}$

Definition using the epsilon delta criterion. is called continuously in , if for each one exists, so that for all with ${\displaystyle f}$ ${\displaystyle x_{0}}$ ${\displaystyle \varepsilon >0}$ ${\displaystyle \delta >0}$ ${\displaystyle x\in D_{f}}$

${\displaystyle |x-x_{0}|<\delta }$

applies:

${\displaystyle |f(x)-f(x_{0})|<\varepsilon }$.

Intuitively, the condition of continuity means that for every change in the function value that one is willing to accept, a maximum change can be found in the argument that ensures this specification. ${\displaystyle \varepsilon }$ ${\displaystyle \delta }$

Example: Proof of the continuity of the function at the point ${\displaystyle f(x)=2x+3}$ ${\displaystyle x_{0}}$

---

Be and with ${\displaystyle x,x_{0}\in \mathbb {R} }$ ${\displaystyle \varepsilon \in \mathbb {R} }$

${\displaystyle \varepsilon >0}$.

It is

${\displaystyle |f(x)-f(x_{0})|=|(2x+3)-(2x_{0}+3)|=|2x-2x_{0}|=2|x-x_{0}|}$.

So that this is less than the specified number , z. B. ${\displaystyle \varepsilon }$

${\displaystyle \delta (\varepsilon )={\tfrac {1}{2}}\varepsilon }$

to get voted. Because from

${\displaystyle |x-x_{0}|<\delta ={\tfrac {1}{2}}\varepsilon }$

then follows namely

${\displaystyle |f(x)-f(x_{0})|=2|x-x_{0}|<2\cdot {\tfrac {1}{2}}\varepsilon =\varepsilon }$.

Remarks:

• Since the function is continuous at every point , it is therefore completely continuous. ${\displaystyle f}$ ${\displaystyle x_{0}\in \mathbb {R} }$ ${\displaystyle f}$ ${\displaystyle \mathbb {R} }$
• Because only by , but not from the place depends, is even quite uniformly continuous . ${\displaystyle \delta }$ ${\displaystyle \varepsilon }$ ${\displaystyle x_{0}\in \mathbb {R} }$ ${\displaystyle f}$ ${\displaystyle \mathbb {R} }$

Example for the sequence criterion: The sequence exp (1 / n ) converges to exp (0)

Definition using limit values. With this definition one demands the interchangeability of function execution and limit value generation. Here you can either rely on the concept of limit values for functions or for consequences .
In the first case we formulate: is called continuous in if the limit value exists and corresponds to the function value, i.e. if: ${\displaystyle f}$ ${\displaystyle x_{0}}$ ${\displaystyle \lim _{x\to x_{0}}f(x)}$ ${\displaystyle f(x_{0})}$

${\displaystyle \lim _{x\to x_{0}}f(x)=f(x_{0})}$.

In the second case one formulates: is called continuous in , if for every convergent sequence with elements , the sequence converges against . The second condition is also known as the sequence criterion . ${\displaystyle f}$ ${\displaystyle x_{0}}$ ${\displaystyle x_{0}}$ ${\displaystyle (a_{n})}$ ${\displaystyle a_{n}\in D_{f}}$ ${\displaystyle {\bigl (}f(a_{n}){\bigr )}}$ ${\displaystyle f(x_{0})}$

Instead of continuity in one often speaks of continuity in point or continuity in place . If this condition is not met, it is called discontinuous in (in the point / at the point) , or referred to as a discontinuity of . ${\displaystyle x_{0}}$ ${\displaystyle x_{0}}$ ${\displaystyle x_{0}}$ ${\displaystyle f}$ ${\displaystyle x_{0}}$ ${\displaystyle x_{0}}$ ${\displaystyle f}$

One speaks of a continuous function if the function is continuous in every point of its domain.

Examples of continuous and discontinuous functions

If a function is differentiable at one point , it is also continuous there. This is followed in particular by continuity

• of all rational functions (i.e. about or ) ${\displaystyle x\mapsto x^{3}+4x^{2}-6x+9}$ ${\displaystyle x\mapsto {\frac {2x-1}{x+2}}}$
• of exponential functions , for solid ${\displaystyle x\mapsto a^{x}}$ ${\displaystyle a\in \mathbb {R} ^{>0}}$
• the trigonometric functions (i.e. sine , cosine, tangent , ...)
• of the logarithmic functions

The continuity of these functions can, however, also be proven directly without recourse to the concept of differentiability.

The amount function is also continuous, even if it is not differentiable at point 0. All power functions are also continuous (approximately ), although they are also not differentiable for an exponent less than 1 at point 0. In fact, all elementary functions are continuous (for example ). ${\displaystyle x\mapsto x^{\frac {1}{2}}={\sqrt {x}}}$
${\displaystyle x\mapsto {\sqrt {1+\cos ^{2}(x-5)}}}$

The graph of a continuous rational function . The function is not defined for . ${\displaystyle x=-2}$

When considering the elementary functions, however, it should be noted that some elementary functions only have a real subset of the real numbers as a domain. The square root function z. B. omitted all negative numbers, with the tangent function all zeros of the cosine.
In these cases it is sometimes formulated imprecisely that the functions are discontinuous in the corresponding places. However, this is not correct, since the question of continuity only arises for points in the domain of definition. Mathematically, however, the question of a continuous continuation of the function at a definition gap makes sense .
For example, the function is

${\displaystyle x\mapsto {\frac {2x-1}{x+2}}}$

defined for all real numbers and continuously in every point of their domain. So it is a continuous function. The question of continuity in does not arise because this point does not belong to the domain of definition. A steady continuation of the function at this definition gap is not possible. ${\displaystyle x\not =-2}$ ${\displaystyle x=-2}$

The absolute value and the square root functions are examples of continuous functions that cannot be differentiated at individual points in the domain. At the beginning of the 19th century, the mathematical experts still assumed that a continuous function had to be differentiable at least in "most" places. Bernard Bolzano was the first mathematician to construct a function that is continuous everywhere but nowhere differentiable, the Bolzano function . However, he did not publish his result. Karl Weierstrass then also found such a function known as the Weierstrass function in the 1860s , with which he caused a sensation in the mathematical world. The graph of the Weierstrass function cannot effectively be drawn. This shows that the intuitive explanation that a continuous function is a function whose graph can be drawn without removing the pen can be misleading. Ultimately, when examining the properties of continuous functions, one always has to fall back on the exact definition.

Using mathematical methods from the 20th century, it was even possible to show that the functions that are nowhere differentiable are, in a certain sense, "often" among the continuous functions.

The sign function is not continuous at the 0 position. ${\displaystyle \operatorname {sgn}(x)}$

Simple examples of discontinuous functions are:

• the sign function (discontinuous only in 0)
• the Dirichlet function (discontinuous at every point)
• the Thoma's function (discontinuously exact in all rational numbers).

Continuity of compound functions

Similar to differentiability, continuity is a property that is transferred from the components to the functions that are composed of them in many operations. The continuity of in is already given for the following points . ${\displaystyle f}$ ${\displaystyle x_{0}}$

• Execution one after the other : If there is another real function whose domain includes the range of values and which is continuous in, then the composition is continuous in . ${\displaystyle g}$ ${\displaystyle f}$ ${\displaystyle f(x_{0})}$ ${\displaystyle g\circ f}$ ${\displaystyle x_{0}}$
• Algebraic operations: Is another real function with the same domain as that also is continuous, then the point-defined functions , , and also steadily . In the latter case should be noted, however, that the domain of the composite function as without the zero set of results. In particular, even in this case there must not be a zero of . ${\displaystyle g}$ ${\displaystyle f}$ ${\displaystyle x_{0}}$ ${\displaystyle f+g}$ ${\displaystyle f-g}$ ${\displaystyle f\cdot g}$ ${\displaystyle {\tfrac {f}{g}}}$ ${\displaystyle x_{0}}$ ${\displaystyle D_{f}}$ ${\displaystyle g}$ ${\displaystyle x_{0}}$ ${\displaystyle g}$
• Maximum / Minimum: Under the same conditions as in the previous point, the functions defined point by point and are continuous in . ${\displaystyle \max(f,g)}$ ${\displaystyle \min(f,g)}$ ${\displaystyle x_{0}}$

If the areas of definition of the functions involved do not fit together as required, you may be able to help yourself further by restricting the areas of definition.

Under certain conditions, continuity is also carried over to the inverse function . However, the statement here cannot be formulated for point-wise continuity:

If the domain of the injective , continuous real function is an interval, the function is strictly monotonic (rising or falling). The inverse function defined on the range of values is also continuous. ${\displaystyle f}$ ${\displaystyle f}$ ${\displaystyle f^{-1}}$

With the help of these permanent properties, for example, the continuity of the elementary function given above can be derived from the continuity of the cosine, the identical function and the constant functions . If one generalizes this consideration, then the continuity of all elementary functions results as a consequence of the simple examples given above. ${\displaystyle x\mapsto {\sqrt {1+\cos ^{2}(x-5)}}}$

Laws about continuous real functions

There are a number of important theorems that apply to continuous real functions . The easiest way to formulate these is to assume that with is a closed, bounded interval: ${\displaystyle f}$ ${\displaystyle D_{f}=[a,b]}$ ${\displaystyle a,b\in \mathbb {R} ,a<b}$

• Intermediate value theorem : The function takes any value between and . ${\displaystyle f(a)}$ ${\displaystyle f(b)}$

• Theorem of minimum and maximum : is restricted and the infimum and supremum of its function values ​​are also taken as function values. So it is actually a matter of minimum and maximum . This theorem proved by Weierstrass , sometimes also called the extreme value theorem, only provides the existence of these extreme values . Statements from differential calculus are often required to find them in practice . ${\displaystyle f}$

• Fundamental theorem of analysis : is Riemann integrable and the integral function ${\displaystyle f}$

${\displaystyle F(x)=\int _{a}^{x}f(t)\,{\rm {d}}t}$

is an antiderivative of . ${\displaystyle f}$

• Heine's theorem : fulfills a stricter version of the epsilon-delta criterion. The corresponding property is called uniform continuity . ${\displaystyle f}$

From the interim value theorem and theorem of minimum and maximum together it follows that the image of is also a closed, bounded interval (or in the case of a constant function a one-point set). ${\displaystyle f}$

Other concepts of continuity

Tightening of the concept of continuity are z. B. uniform continuity , (local) Lipschitz continuity , Hölder continuity as well as absolute continuity and geometric continuity . Ordinary continuity is sometimes referred to as point-wise continuity in order to distinguish it from uniform continuity. Applications of the Lipschitz continuity can be found e.g. B. in existence and uniqueness theorems (e.g. Picard-Lindelöf theorem ) for initial value problems of ordinary differential equations and in geometric measure theory . Absolute continuity is used in stochastics and measure theory , and geometric continuity in geometric modeling .

One property that a set of functions can have is uniformity . It plays a role in the frequently used phrase by Arzelà-Ascoli .

Continuity for functions of several variables

One function

${\displaystyle f\colon \mathbb {R} ^{n}\to \mathbb {R} }$

${\displaystyle (x_{1},\ldots ,x_{n})\mapsto f(x_{1},\ldots ,x_{n})}$

is called continuous in , if for every converging sequence the sequence of the function values ​​converges to. ${\displaystyle (x_{1},\ldots ,x_{n})}$ ${\displaystyle (x_{1},\ldots ,x_{n})}$ ${\displaystyle f(x_{1},\ldots ,x_{n})}$

It is called continuous if it is continuous in every point of the domain.

If the function is continuous, it is also continuous in every argument. ${\displaystyle f}$

The function is called continuous in the first argument if the function is for each ${\displaystyle f}$ ${\displaystyle (x_{2},\ldots ,x_{n})\in \mathbb {R} ^{n-1}}$

${\displaystyle f_{(x_{2},\ldots ,x_{n})}\colon \mathbb {R} \to \mathbb {R} }$

${\displaystyle x\mapsto f(x,x_{2},\ldots ,x_{n})}$

is steady. Similarly, the continuity is defined in the second, third, ..., -th argument. ${\displaystyle n}$

Representation of the not continuous function f at point (0,0) .

Conversely, the continuity of does not follow from the continuity in every argument , as the following example shows: ${\displaystyle f}$

${\displaystyle f\colon \mathbb {R} ^{2}\to \mathbb {R} ,\quad (x,y)\mapsto {\begin{cases}0,&x=y=0\\{\frac {xy}{x^{2}+y^{2}}},&{\text{sonst}}\end{cases}}}$

It is easy to be convinced that this function is continuous in both arguments. The function is discontinuous at the point . If one defines for , then there is a sequence which converges in against . It applies to everyone . The image sequence thus has the constant value and therefore does not converge towards the function value 0 at the point under consideration. ${\displaystyle (0,0)}$ ${\displaystyle a_{k}=\left({\tfrac {1}{k}},{\tfrac {1}{k}}\right)}$ ${\displaystyle k\in \mathbb {N} }$ ${\displaystyle (a_{k})_{k\in \mathbb {N} }}$ ${\displaystyle \mathbb {R} ^{2}}$ ${\displaystyle (0,0)}$ ${\displaystyle f(a_{k})={\tfrac {1}{2}}}$ ${\displaystyle k\in \mathbb {N} }$ ${\displaystyle {\tfrac {1}{2}}}$

Continuity for mappings between metric spaces

definition

Be and metric spaces, a figure and . ${\displaystyle \left(X,d_{X}\right)}$ ${\displaystyle \left(Y,d_{Y}\right)}$ ${\displaystyle f\colon X\to Y}$ ${\displaystyle x\in X}$

Then continuous is called in if it always follows from. This condition is again equivalent to the criterion. ${\displaystyle f}$ ${\displaystyle x}$ ${\displaystyle \lim _{n\to \infty }x_{n}=x}$ ${\displaystyle \lim _{n\to \infty }f(x_{n})=f(x)}$ ${\displaystyle \epsilon -\delta -}$

The mapping is called continuous if it is continuous at every point . ${\displaystyle f}$ ${\displaystyle x\in X}$

Mapping between finite-dimensional Euclidean vector spaces

An illustration

${\displaystyle f=(f_{1},\ldots ,f_{m})\colon \mathbb {R} ^{n}\to \mathbb {R} ^{m}}$

is continuous in in the sense of this definition if and only if the component mappings are all continuous in . ${\displaystyle x=(x_{1},\ldots ,x_{n})}$ ${\displaystyle f_{1},\ldots ,f_{m}\colon \mathbb {R} ^{n}\to \mathbb {R} }$ ${\displaystyle x}$

Mapping between normalized vector spaces

→ Main article : Bounded operator

A linear operator

${\displaystyle T\colon V\rightarrow W}$

between normalized vector spaces is continuous if and only if it is bounded , i.e. if there is a constant such that ${\displaystyle K}$

${\displaystyle \|T(x)\|\leq K\|x\|}$

for everyone . This characterization also applies more generally to images between bornological spaces . ${\displaystyle x\in V}$

If and even are Banach spaces, the theorem of a closed graph can often be used to prove continuity. ${\displaystyle V}$ ${\displaystyle W}$

More generally, one can also define continuity for mappings between locally convex vector spaces and then it is continuous if and only if for every continuous seminorm on the seminorm is continuous on . ${\displaystyle f}$ ${\displaystyle p}$ ${\displaystyle Y}$ ${\displaystyle p\circ f}$ ${\displaystyle X}$

Continuity of limit values ​​of function sequences

In general, the point-wise convergence of a sequence of continuous functions does not result in the continuity of the limit function . For example, for the sequence of functions, it converges towards the discontinuous function . ${\displaystyle (f_{k}\colon X\to Y)_{k\in N}}$ ${\displaystyle f\colon X\to Y}$ ${\displaystyle X=Y=[0,1]}$ ${\displaystyle f_{k}(x)=x^{k}}$ ${\displaystyle \lim _{k\to \infty }f_{k}(x)={\begin{cases}1&x=1\\0&\mathrm {sonst} \end{cases}}}$

Under stricter convergence terms for function sequences , in particular the (locally) uniform convergence , the continuity of the limit function can always be ensured.

With the help of this concept of convergence of function sequences, the continuity of complex functions defined by power series can be proven inside their convergence circle (see also Abelian limit theorem ).

The Banach-Steinhaus theorem ensures the continuity of the limit function if and are Banach spaces and all are linear operators. ${\displaystyle X}$ ${\displaystyle Y}$ ${\displaystyle f_{k}}$

Variants of the concept of continuity

For functions between metric spaces there are a number of other continuity terms, each of which places stricter conditions on how much the function value may fluctuate depending on the fluctuation in the argument. The following should be mentioned here: uniform continuity (can also be defined for functions on uniform spaces), (local) Lipschitz continuity , Hölder continuity , uniform continuity and (if the domain is a real interval) absolute continuity .

Consistency in the topology

The concept of continuity was initially developed for real and complex functions. When justifying the mathematical sub-area of ​​topology, however, it became apparent that the concept can of course be extended to this area. Since then, continuity has been one of the basic concepts of modern mathematics.

The alternative definitions of continuity given above can easily be extended to much more general situations, and much of the given properties of continuous functions can also be generalized. This generalized concept of continuity is of central importance for topology and related mathematical sub-areas (such as functional analysis ).

Definitions of continuity

Since topological spaces can be defined in different (but equivalent) ways, there are also several equivalent definitions of continuity. In the following there are several variants for each definition, which differ in their degree of formalization, but say the same in terms of content.

Functions have a definition range and a target set that can be provided with different topologies. The choice of these topologies is not part of the 'identity' of the function but is essential for the question of continuity. It is therefore actually imprecise to say that a function is continuous or discontinuous.

A precise formulation of the definition given below by means of surroundings would for example read:

Be and topological spaces. Be a function and . Then continuous in is called with respect to the spaces and if for every -surrounding of the archetype is a -surrounding of . ${\displaystyle (X,T_{1})}$ ${\displaystyle (Y,T_{2})}$ ${\displaystyle f\colon X\to Y}$ ${\displaystyle \xi \in X}$ ${\displaystyle f}$ ${\displaystyle \xi }$ ${\displaystyle (X,T_{1})}$ ${\displaystyle (Y,T_{2})}$ ${\displaystyle (Y,T_{2})}$ ${\displaystyle U}$ ${\displaystyle f(\xi )}$ ${\displaystyle f^{-1}(U)}$ ${\displaystyle (X,T_{1})}$ ${\displaystyle \xi }$

In mathematical practice, it is almost always clear which topologies should be used in the respective rooms. Hence, the somewhat imprecise speech used in this article is common. In the rare cases where several topologies are available, this is made clear by appropriate explanations.

Open sets

1. A function between two topological spaces is continuous if and only if the archetypes of open sets are open sets again.
2. Let be a mapping from the topological space into the topological space . Then that means continuous if the inverse image under by everyone in open set open again in is. ${\displaystyle f}$ ${\displaystyle X}$ ${\displaystyle Y}$ ${\displaystyle f}$ ${\displaystyle f}$ ${\displaystyle Y}$ ${\displaystyle O}$ ${\displaystyle X}$
3. ${\displaystyle f\colon X\rightarrow Y}$continuous   (where the topology of the space , i.e. the set of open sets of the topological space) ${\displaystyle \Leftrightarrow \ \forall O\in {\mathcal {O}}_{Y}:f^{-1}(O)\in {\mathcal {O}}_{X}}$ ${\displaystyle {\mathcal {O}}_{Y}}$ ${\displaystyle Y}$

Closed sets

The continuity can be defined by closed sets by replacing "open sets" in the definition above with "closed sets":

1. A function between two topological spaces is continuous if and only if the archetypes of closed sets are closed sets.
2. Let be a mapping from the topological space into the topological space . Then that means continuous if the inverse image under by everyone in closed set closed again is. ${\displaystyle f}$ ${\displaystyle X}$ ${\displaystyle Y}$ ${\displaystyle f}$ ${\displaystyle f}$ ${\displaystyle Y}$ ${\displaystyle A}$ ${\displaystyle X}$
3. ${\displaystyle f\colon X\rightarrow Y}$ steadily   ${\displaystyle \Leftrightarrow \ \forall O\in {\mathcal {O}}_{Y}:X\setminus f^{-1}(Y\setminus O)\in {\mathcal {O}}_{X}}$

Continuity at a point x : for every neighborhood V of f ( x ) there is a neighborhood U of x with f ( U ) ⊆ V

Environments

Let be the set of all neighborhoods of a point . ${\displaystyle {\mathcal {U}}(x)}$ ${\displaystyle x}$

1. A function between two topological spaces is continuous if, for every point, the following applies: for every area around the image point of this point there is an area around the point, the image of which lies completely in the area around the image point.
2. Let be a mapping from the topological space into the topological space . Then is continuous if and only if for every point in holds: If there is a neighborhood of , then there is a neighborhood of such that in is contained. ${\displaystyle f}$ ${\displaystyle X}$ ${\displaystyle Y}$ ${\displaystyle f}$ ${\displaystyle x}$ ${\displaystyle X}$ ${\displaystyle U}$ ${\displaystyle f(x)}$ ${\displaystyle V}$ ${\displaystyle x}$ ${\displaystyle f(V)}$ ${\displaystyle U}$
3. ${\displaystyle f\colon X\rightarrow Y}$ steadily   ${\displaystyle \Leftrightarrow \ \forall x\in X\ \forall U\in {\mathcal {U}}(f(x))\exists V\in {\mathcal {U}}(x):f(V)\subseteq U}$

Networks

For a directed set and a set , a network is a picture . Usually you write analogously to episodes . Since the natural numbers form a directed set with the usual arrangement, sequences are special networks. ${\displaystyle (I,\triangleleft )}$ ${\displaystyle X}$ ${\displaystyle x\colon I\to X}$ ${\displaystyle (x_{i})_{i\in I}}$

1. Be and topological spaces. An illustration is continuous if for all true: For every in to converging network , the network converges in against ${\displaystyle X}$ ${\displaystyle Y}$ ${\displaystyle f\colon X\to Y}$ ${\displaystyle x\in X}$ ${\displaystyle X}$ ${\displaystyle x}$ ${\displaystyle (x_{i})_{i\in I}}$ ${\displaystyle \left(f(x_{i})\right)_{i\in I}}$ ${\displaystyle Y}$ ${\displaystyle f(x).}$
2. ${\displaystyle f\colon X\to Y}$ steadily   ${\displaystyle \Leftrightarrow \ \forall x\in X\colon \left((x_{i})_{i\in I}\longrightarrow _{X}x\Rightarrow \left(f(x_{i})\right)_{i\in I}\longrightarrow _{Y}f(x)\right).}$

Functions that fulfill the weaker condition “ ” are named continuously in . If the first axiom of countability is fulfilled (this is the case e.g. for metric spaces), then the two terms are equivalent. ${\displaystyle (x_{n})_{n\in \mathbb {N} }\to x\Longrightarrow (f(x_{n}))_{n\in \mathbb {N} }\to f(x)}$ ${\displaystyle x}$ ${\displaystyle X}$

graduation

1. A function between two topological spaces is continuous if and only if the image of the termination of any subset is contained in the termination of the image of this subset.
2. Let be a mapping from the topological space into the topological space . Then is continuous if and only if for every subset of : The image of the closure of lies in the closure of the image of . ${\displaystyle f}$ ${\displaystyle X}$ ${\displaystyle Y}$ ${\displaystyle f}$ ${\displaystyle A}$ ${\displaystyle X}$ ${\displaystyle A}$ ${\displaystyle A}$
3. ${\displaystyle f\colon X\rightarrow Y}$ steadily   ${\displaystyle \Leftrightarrow \ \forall A\subseteq X:f({\overline {A}})\subseteq {\overline {f(A)}}}$

If one does not consider the archetypes of a function, as in the case of continuity, but the images of the function, one arrives at the terms of the open or closed mapping .

Properties of continuous functions

• If and are continuous functions, then the composition is also continuous. ${\displaystyle f\colon X\to Y}$ ${\displaystyle g\colon Y\to Z}$ ${\displaystyle g\circ f\colon X\to Z}$
• Constraints on continuous functions are continuous.
• If steady and ${\displaystyle f\colon X\to Y}$
  • X is compact , then is compact. ${\displaystyle f(X)}$
  • X continuous , then is connected. ${\displaystyle f(X)}$
  • X is path-connected , then is path-connected. ${\displaystyle f(X)}$
• Continuity is a local property.

Many important theorems about functions assume that they are continuous. Here are some examples:

• Borel is a continuous function - measurable .

• The Peano existence theorem on the existence of solutions of ordinary differential equations requires the continuity of the right side.

• Brouwer's degree of mapping, which is important in topology, and its generalizations used in functional analysis are defined for continuous mapping.

• A continuous function of a non-empty, compact and convex subset of a Hausdorff topological vector space in itself has a fixed point ( Schauder's fixed point theorem ).

Examples of continuous functions

Elementary examples

• For a set of definitions with the discrete topology , every function is continuous in any space . ${\displaystyle X}$ ${\displaystyle f\colon X\to Y}$ ${\displaystyle Y}$
• For a target set with the indiscreet topology , every function in this space is continuous. ${\displaystyle Y}$ ${\displaystyle f\colon X\to Y}$ ${\displaystyle Y}$
• Constant mappings between any topological spaces are always continuous.
• For a definition set with the indiscrete topology and a target set that is a T ₀ space , the constant functions are the only continuous functions.
• The identical mapping is continuous if the topology of the original image space is finer than that of the image space, i.e. H. . ${\displaystyle \operatorname {id} _{X}\colon (X,{\mathcal {T}}_{1})\to (X,{\mathcal {T}}_{2}),x\mapsto x}$ ${\displaystyle {\mathcal {T}}_{2}\subseteq {\mathcal {T}}_{1}}$

ways

→ Main article : Path (mathematics)

If a topological space is a continuous function from to is also called a path in . This term itself is of great importance in various areas of mathematics: ${\displaystyle X}$ ${\displaystyle [0,1]}$ ${\displaystyle X}$ ${\displaystyle X}$

• Definition of the curve integral
• Definition of the route context
• Definition of the fundamental group

The result may be surprising that the n-dimensional unit cube can be completely filled for each by a path ( Peano curve ). ${\displaystyle [0,1]^{n}}$ ${\displaystyle n\in \mathbb {N} }$

Homeomorphisms

→ Main article : Homeomorphism

In algebra, the inverse function of a bijective homomorphism is again a homomorphism. By definition, homomorphisms are characterized by the fact that their application can be interchanged with the execution of the arithmetic operations. When proving the homomorphism property of the inverse function, one takes advantage of the fact that the arithmetic operations can always be carried out (in the domain of definition) and always have a clear result (in the target set). A continuous function can be characterized as a function, the application of which can be interchanged with the limit value formation (of networks). However, since networks do not have to converge in the domain of definition and networks can also converge to several limit values ​​in the target set, an analogous statement about inverse functions does not apply here. This shows, for example, the bijective continuous function . A bijective function between two topological spaces is called homeomorphism if one (and thus all) of the following equivalent conditions is met: ${\displaystyle \varphi \colon [0,1[\rightarrow \{z\in \mathbb {C} \,||z|=1\},x\mapsto e^{2\pi ix}}$

(a) The function and its inverse function are continuous.
(b) The function and its inverse function are open.
(c) The function and its inverse function are complete.
(d) The function is continuous and open.
(e) The function is continuous and closed.

Every continuous bijection between compact Hausdorff spaces is a homeomorphism.

Functions of several variables

A function whose domain is a Cartesian product is also called a function in several variables. The following explanations for the case of a product of two topological spaces can be extended to any (also infinite) products.

Let , and be topological spaces and a function in two variables. ${\displaystyle X}$ ${\displaystyle Y}$ ${\displaystyle Z}$ ${\displaystyle f\colon X\times Y\to Z}$

${\displaystyle f}$is called continuous in the first argument if the function is continuous for each . The continuity is defined in the same way in the second argument. ${\displaystyle y_{0}\in Y}$ ${\displaystyle f_{y_{0}}\colon X\to Z,x\mapsto f(x,y_{0})}$

If the function is continuous ( the product topology is assumed here), then is also continuous in both arguments. The reverse does not apply, as the example in Continuous Functions in Several Variables shows. ${\displaystyle f}$ ${\displaystyle X\times Y}$ ${\displaystyle f}$

The opposite situation is much simpler: for a function there are (clearly defined) functions and so for all . Then is continuous if and only if and there are. So you can identify with in a natural way . ${\displaystyle f\colon X\to Y\times Z}$ ${\displaystyle g\colon X\to Y}$ ${\displaystyle h\colon X\to Z}$ ${\displaystyle f(x)=(g(x),h(x))}$ ${\displaystyle x\in X}$ ${\displaystyle f}$ ${\displaystyle g}$ ${\displaystyle h}$ ${\displaystyle C(X,Y\times Z)}$ ${\displaystyle C(X,Y)\times C(X,Z)}$

Set of continuous functions

The set of all continuous functions from to is usually denoted by or . The C stands for "continuous", English for "steady". If the picture space is evident from the context or , one often only writes or . ${\displaystyle X}$ ${\displaystyle Y}$ ${\displaystyle C(X,Y)}$ ${\displaystyle C^{0}(X,Y)}$ ${\displaystyle Y}$ ${\displaystyle Y=\mathbb {C} }$ ${\displaystyle C(X)}$ ${\displaystyle C^{0}(X)}$

${\displaystyle C(X)}$is a sub- algebra of the -Algebra of all real-valued functions . Two continuous functions from to already match if they match on a dense subset of . Since every subset of has at most a countable dense subset, one can deduce from this that the thickness of is the thickness of the continuum (if it is not empty). The set of all functions from to has a much greater power (at least if there is an interval with more than one element). One can interpret this to mean that continuity is a 'rare' property among real functions. This somewhat contradicts everyday experience, since all elementary functions are continuous. ${\displaystyle \mathbb {C} }$ ${\displaystyle X}$ ${\displaystyle X}$ ${\displaystyle Y}$ ${\displaystyle X}$ ${\displaystyle \mathbb {C} }$ ${\displaystyle C(X)}$ ${\displaystyle X}$ ${\displaystyle X}$ ${\displaystyle \mathbb {C} }$ ${\displaystyle X}$

Important subspaces of are for example: ${\displaystyle C(X)}$

• the continuous functions with a compact carrier ${\displaystyle C_{c}(X)}$

• the continuous functions that vanish at infinity ${\displaystyle C_{0}(X)}$

• the bounded continuous functions . ${\displaystyle C_{b}(X)}$

• if is a differentiable manifold : the set of continuously differentiable functions and ${\displaystyle X}$ ${\displaystyle C^{1}(X)}$

• the set of functions that can be differentiated as often as desired . ${\displaystyle C^{\infty }(X)}$

Is a compact space , the continuous functions carry more structure. If then, in addition, there is a metric space , for example again , then the continuous functions are always a subset of the restricted functions , so it is true ${\displaystyle X}$ ${\displaystyle Y}$ ${\displaystyle Y=\mathbb {R} }$

${\displaystyle C(X,Y)\subset B(X,Y)}$.

If a standard is defined, then via ${\displaystyle Y}$ ${\displaystyle \|\cdot \|_{Y}}$

${\displaystyle \|f\|_{\sup }:=\sup _{x\in X}\|f(x)\|_{Y}}$

a norm is defined, the so-called supremum norm . This definition makes sense due to the limitation of continuous functions in compact spaces. ${\displaystyle C(X,Y)}$

If a Banach space , i.e. a completely standardized space, is also a Banach space. The continuous functions are then a closed subspace of the bounded functions. ${\displaystyle Y}$ ${\displaystyle C(X,Y)}$

For a family of continuous functions, one can search for a topology as coarse as possible in the domain of definition, with regard to which the functions are still continuous, or for the target set for the finest possible one. These topologies are called the initial topology and the final topology .

Algebras of continuous complex-valued functions

For a topological space is , the set of continuous complex-valued functions , as already noted, an algebra. This is of course commutative and unital (the function with the constant value 1 is the unity element). ${\displaystyle X}$ ${\displaystyle C(X)}$ ${\displaystyle X}$ ${\displaystyle \mathbb {C} }$

In addition, a conjugate linear involution is naturally given in this algebra , which is also compatible with multiplication. This is given by for . ${\displaystyle {\overline {f}}(x)={\overline {f(x)}}}$ ${\displaystyle x\in X,f\in C(X)}$

${\displaystyle C(X)}$is therefore a unital , commutative * -algebra . Note that the study of these algebras includes the study of the algebras of all complex-valued functions on an arbitrary set, since any set can be given the discrete topology, making all functions continuous.

The lemma Urysohn ensures most important topological spaces that is sufficiently rich. In fact, this algebra often turns out to be too large for practical investigation. One therefore usually goes to the unital * -sub algebra of bounded, continuous complex-valued functions on . If is compact, then because of (15 '). ${\displaystyle C(X)}$ ${\displaystyle C_{b}(X)}$ ${\displaystyle X}$ ${\displaystyle X}$ ${\displaystyle C(X)=C_{b}(X)}$

${\displaystyle C_{b}(X)}$becomes a commutative, unital C * algebra through the supremum norm .

The Gelfand-Neumark theorem states that every commutative, unital C * -algebra is isomorphic to for a suitably chosen compact Hausdorff space . Except for homeomorphism, it is clearly determined (and the theorem also specifies a constructive method for determining ). Thus the theory of the commutative, unital C * -algebras can be fully identified with the theory of compact Hausdorff spaces. This is a powerful tool because statements that are difficult to prove in one theory can be carried over to the other where it is often much easier to prove. ${\displaystyle C(K)}$ ${\displaystyle K}$ ${\displaystyle K}$ ${\displaystyle K}$

As an extension of this result, the theory of commutative, possibly not unital, C * -algebras can be identified with the theory of locally compact Hausdorff spaces. Here, however, a locally compact Hausdorff space is not , but the subalgebra of C ₀ functions to be considered. ${\displaystyle X}$ ${\displaystyle C_{b}(X)}$ ${\displaystyle X}$

Note: Using the GNS construction , every non-commutative C * -algebra can also be identified with an algebra of continuous (linear) functions. Here, however, the composition of operators is used as multiplication and not point-by-point multiplication. Therefore, these two approaches should not be confused with one another.

Two further important results about the structure of for compact Hausdorff spaces are the Stone-Weierstraß theorem (characterization of the dense * -subalgebras of ) and the Arzelà-Ascoli theorem (characterization of the relatively compact subsets of ). A special case of the first theorem is Weierstrass's approximation theorem, which states that on a compact subset of every continuous, complex-valued function can be uniformly approximated by a sequence of polynomial functions. ${\displaystyle C(K)}$ ${\displaystyle K}$ ${\displaystyle C(K)}$ ${\displaystyle C(K)}$ ${\displaystyle \mathbb {R} }$

Linking algebraic and topological structures

Many of the sets studied in mathematics naturally have both a topological and an algebraic structure. A simple example of this are the quantities and , which become metric spaces through the amount metric, and which at the same time become solids through the basic arithmetic operations. A particularly rich theory emerges when these two structures harmonize. This is the case if the link (s) that define the algebraic structure are continuous functions with regard to the topology under consideration. In this way, the definition of a topological group , a topological ring / body and a topological vector space result very easily . ${\displaystyle \mathbb {R} }$ ${\displaystyle \mathbb {C} }$

If one has two examples of such a category (i.e. two topological groups), it is advisable to examine the functions between these two, which are compatible with both structures, which are therefore continuous homomorphisms. In functional analysis, for example, the properties of (spaces of) continuous linear operators are intensively examined. Incidentally, in all of the categories mentioned, a homomorphism is either continuous or discontinuous at every point.

With the axiom of choice one can construct numerous discontinuous homomorphisms between topological groups, in particular also numerous discontinuous homomorphisms . ${\displaystyle f\colon \mathbb {R} \to \mathbb {R} }$

On the other hand, continuous homomorphisms between Lie groups are always differentiable.

history

At the beginning of the 19th century, Augustin-Louis Cauchy and Bernard Bolzano independently gave a definition of continuity. Their concept of continuity differed fundamentally from Euler's, according to which a function is called continuous if it can be described by a single analytical expression. By an analytic expression, Euler understood expressions that are formed by finite (algebraic functions) or infinite (transcendent functions) application of algebraic operations such as addition, subtraction, multiplication, division, extraction of the roots. In Euler's sense, the absolute value function was considered discontinuous because it was given by two analytical expressions, while according to the definition going back to Cauchy and Bolzano, this function is continuous.

Cauchy and Bolzano called a function continuous when sufficiently small changes in the argument only resulted in small changes in the function value. This was already an exact definition, but in its practical application it leaves certain questions unanswered. The - criterion common today was used by Karl Weierstrass in his four-semester lecture cycle, which he gave a total of sixteen times between 1857 and 1887. ${\displaystyle \varepsilon }$ ${\displaystyle \delta }$

For a long time it was unclear whether there are also continuous real functions that are nowhere differentiable. The first example of a real continuous but nowhere differentiable function was constructed by Bernard Bolzano ( Bolzano function ). However, this example was published much later. The existence of such functions became known through Karl Weierstrass (Weierstrass function), who surprised many contemporary mathematicians with it.

See also

• Oscillation of a function
• Continuity in non-standard analysis
• Point of discontinuity
• Definition gap
• Eliminable definition gap
• Left- and right-sided continuity
• Pole position
• Constant differentiability and higher derivatives
• Order-theoretical concept of continuity

literature

• Harro Heuser : Textbook of Analysis . Teubner, Wiesbaden 2003, ISBN 3-519-62233-5
• Theodor Bröcker : Analysis I . Spektrum Akademischer Verlag 1995, ISBN 9783860254172
• Stefan Hildebrandt : Analysis . Springer, Berlin a. a. 2002, ISBN 3-540-42838-0
• Helmut Fischer, Helmut Kaul: Mathematics for Physicists: Volume 1 , Teubner Study Books Mathematics, ISBN 9783835101654

• Boto von Querenburg : Set theoretical topology (=  Springer textbook ). 3rd, revised and expanded edition. Springer-Verlag , Berlin [a. a.] 2001, ISBN 3-540-67790-9 .
• Friedrich Hirzebruch / Winfried Scharlau : Introduction to Functional Analysis (=  series "BI Hochschultaschenbücher" band No . Band 296 ). Bibliographisches Institut , Mannheim [u. a.] 1971, ISBN 3-411-00296-4 . MR0463864
• Horst Schubert : Topology. An introduction (=  mathematical guidelines ). 4th edition. BG Teubner Verlag , Stuttgart 1975, ISBN 3-519-12200-6 . MR0423277

Web links

Wikibooks: Math for non-freaks: Continuity of functions  - learning and teaching materials

Wikibooks: Math for non-freaks: Consequence criterion of continuity: Consequence continuity  - learning and teaching materials

Wikibooks: Math for non-freaks: Epsilon-Delta criterion of continuity  - learning and teaching materials

Commons : Continuity  - collection of images, videos, and audio files

• Short articles on basic concepts of continuity
• Topology without tears by Sidney A. Morris: book on topology for free download (PDF, English)

Individual evidence

1. ↑ B. v. Querenburg, op. Cit., Example 1.31
2. ↑ B. v. Querenburg, op.cit., Sentence 1.30
3. ↑ B. v. Querenburg, op. Cit., Chapter 14C; Hirzebruch-Scharlau, op. Cit., Chapter I.3
4. ↑ B. v. Querenburg, op.cit., Chapter 2
5. ↑ B. v. Querenburg, op.cit., Sentence 8.11
6. ↑ B. v. Querenburg, op.cit., Sentence 4.9
7. ↑ B. v. Querenburg, op. Cit., Example 2.30
8. ↑ B. v. Querenburg, op.cit., Sentence 2.33
9. ↑ B. v. Querenburg, op.cit., Sentence 2.42
10. ↑ B. v. Querenburg, op.cit., Sentence 8.12
11. ↑ B. v. Querenburg, op.cit., Sentence 3.14
12. ↑ Hirzebruch-Scharlau, op.cit., Chapter 3
13. ↑ B. v. Querenburg, op.cit., Chapter 3
14. ↑ Hirzebruch-Scharlau, op.cit., Sentence 29.4
15. ↑ Hildebrandt, op. Cit. Chapter 1.1
16. ↑ Hildebrandt, op.cit., Chapter 2.1
17. ↑ Hildebrandt, op.cit., Chapter 3.1