Curve integral

The curve , line , path or contour integral expands the common concept of integral for integration in the complex plane ( function theory ) or in multi-dimensional space ( vector analysis ).

The path , line or curve over which integration takes place is called the integration path .

Distance integrals over closed curves are also referred to as ring integral , circulation integral or circulation and are written with the symbol . ${\displaystyle \textstyle \oint }$

Real path integrals

Path integral of the first kind

Illustration of a curve integral of the first kind over a scalar field

The path integral of a continuous function ,

${\displaystyle f\colon \mathbb {R} ^{n}\rightarrow \mathbb {R} }$

along a gradually differentiable path

${\displaystyle \gamma \colon [a,b]\to \mathbb {R} ^{n}}$

is defined as

${\displaystyle \int \limits _{\gamma }f\,\mathrm {d} s:=\int \limits _{a}^{b}f(\gamma (t))\;\|{\dot {\gamma }}(t)\|_{2}\;\,\mathrm {d} t.}$

In this case, referred to the derivative of to , and the Euclidean norm of the vector . ${\displaystyle {\dot {\gamma }}}$ ${\displaystyle \gamma }$ ${\displaystyle t}$ ${\displaystyle \|{\dot {\gamma }}(t)\|_{2}}$ ${\displaystyle {\dot {\gamma }}(t)}$

The image set is a piecewise smooth curve in . ${\displaystyle {\mathcal {C}}:=\gamma ([a,b])}$ ${\displaystyle \mathbb {R} ^{n}}$

Remarks

• An example of such a function is a scalar field with Cartesian coordinates . ${\displaystyle f}$
• A path can traverse a curve either as a whole or only in sections several times. ${\displaystyle \gamma }$ ${\displaystyle {\mathcal {C}}}$
• For the path integral of the first kind gives the length of the path . ${\displaystyle f\equiv 1}$ ${\displaystyle \gamma }$
• The path forms u. a. to the starting point of the curve and to its end point. ${\displaystyle \gamma }$ ${\displaystyle a\in \mathbb {R} }$ ${\displaystyle b\in \mathbb {R} }$
• ${\displaystyle t\in [a,b]}$is an element of the definition set of and generally does not represent time. is the associated differential . ${\displaystyle \gamma }$ ${\displaystyle \mathrm {d} t}$

Path integral of the second kind

Illustration of a curve integral of the second kind over a vector field

The path integral over a continuous vector field

${\displaystyle \mathbf {f} \colon \mathbb {R} ^{n}\rightarrow \mathbb {R} ^{n}}$

with a curve parameterized in this way is defined as the integral over the scalar product of and : ${\displaystyle \mathbf {f} \circ \gamma }$ ${\displaystyle {\dot {\gamma }}}$

${\displaystyle \int \limits _{\gamma }\mathbf {f} (\mathbf {x} )\cdot \mathrm {d} \mathbf {x} :=\int \limits _{a}^{b}\mathbf {f} (\gamma (t))\cdot {\dot {\gamma }}(t)\,\mathrm {d} t}$

Influence of the parameterization

If and are simple (ie and are injective ) paths with and and the same image , i.e. if they parameterize the same curve in the same direction and if they traverse the curve exactly once (except for colons), the integrals along and agree. This justifies the name curve integral ; if the direction of integration is evident from the context or is irrelevant, the path in the notation is therefore suppressed. ${\displaystyle \gamma \colon [a,b]\to \mathbb {R} ^{n}}$ ${\displaystyle \eta \colon [c,d]\to \mathbb {R} ^{n}}$ ${\displaystyle \gamma _{|(a,b)}}$ ${\displaystyle \eta _{|(c,d)}}$ ${\displaystyle \gamma (a)=\eta (c)}$ ${\displaystyle \gamma (b)=\eta (d)}$ ${\displaystyle \gamma }$ ${\displaystyle \eta }$

Curve integrals

Since a curve is the image of a path , the definitions of the curve integrals essentially correspond to the path integrals. ${\displaystyle {\mathcal {C}}}$ ${\displaystyle \gamma }$

Curve integral 1st type:

${\displaystyle \int \limits _{\mathcal {C}}f\,\mathrm {d} s:=\int \limits _{a}^{b}f(\gamma (t))\|{\dot {\gamma }}(t)\|_{2}\,\mathrm {d} t.}$

Curve integral 2nd type:

${\displaystyle \int \limits _{\mathcal {C}}\mathbf {f} (\mathbf {x} )\cdot \mathrm {d} \mathbf {x} :=\int \limits _{a}^{b}\mathbf {f} (\gamma (t))\cdot {\dot {\gamma }}(t)\,\mathrm {d} t}$

A special case is again the length of the curve parameterized by : ${\displaystyle \gamma }$ ${\displaystyle {\mathcal {C}}}$

${\displaystyle \mathrm {L{\ddot {a}}nge\ von\ } {\mathcal {C}}=\int \limits _{\mathcal {C}}\mathrm {d} s=\int \limits _{a}^{b}\|{\dot {\gamma }}(t)\|_{2}\,\mathrm {d} t.}$

Path element and length element

The expression appearing in the curve integrals of the first kind

${\displaystyle \mathrm {d} s=\|{\dot {\gamma }}(t)\|_{2}\,\mathrm {d} t}$

is called a scalar path element or length element . The expression appearing in the curve integrals of the second kind

${\displaystyle \mathrm {d} \mathbf {x} ={\dot {\gamma }}(t)\,\mathrm {d} t}$

is called a vectorial path element .

Calculation rules

Let be , curve integrals of the same kind (ie either both of the first or both of the second kind), be the archetype of the two functions and of the same dimension and be . Then the following rules apply to , and : ${\displaystyle \int \limits _{\gamma }\mathbf {f} (\mathbf {x} )}$ ${\displaystyle \int \limits _{\gamma }\mathbf {g} (\mathbf {x} )}$ ${\displaystyle \mathbf {f} }$ ${\displaystyle \mathbf {g} }$ ${\displaystyle \gamma \colon [a,b]\to \mathbb {R} ^{n}}$ ${\displaystyle \alpha }$ ${\displaystyle \beta \in \mathbb {R} }$ ${\displaystyle c\in \mathbb {[} a,b]}$

• ${\displaystyle \alpha \int \limits _{\gamma }\mathbf {f} (\mathbf {x} )+\beta \int \limits _{\gamma }\mathbf {g} (\mathbf {x} )=\int \limits _{\gamma }(\alpha \mathbf {f} (\mathbf {x} )+\beta \mathbf {g} (\mathbf {x} ))}$    (Linearity)

• ${\displaystyle \int \limits _{\gamma }\mathbf {f} (\mathbf {x} )=\int \limits _{\gamma |_{[a,c]}}\mathbf {f} (\mathbf {x} )+\int \limits _{\gamma |_{[c,b]}}\mathbf {f} (\mathbf {x} )}$    (Decomposition additivity)

Notation for curve integrals of closed curves

If the path is closed, one writes ${\displaystyle \gamma }$

instead of also , ${\displaystyle \displaystyle \int \limits _{\gamma }}$ ${\displaystyle \displaystyle \oint \limits _{\gamma }}$

and analog for closed curves ${\displaystyle {\mathcal {C}}}$

instead of too . ${\displaystyle \displaystyle \int \limits _{\mathcal {C}}}$ ${\displaystyle \displaystyle \oint \limits _{\mathcal {C}}}$

With the circle in the integral you want to make it clear that it is closed. The only difference is in the notation. ${\displaystyle \gamma }$

Examples

• If the graph is a function , then this curve becomes through the way ${\displaystyle {\mathcal {C}}}$ ${\displaystyle f\colon [a,b]\to \mathbb {R} }$

${\displaystyle \gamma \colon [a,b]\to \mathbb {R} ^{2},\quad t\mapsto (t,f(t))}$

parameterized. Because of

${\displaystyle \|{\dot {\gamma }}(t)\|_{2}={\sqrt {1+f'(t)^{2}}}}$

the length of the curve is the same

${\displaystyle \int \limits _{\mathcal {C}}\mathrm {d} s=\int \limits _{a}^{b}{\sqrt {1+f'(t)^{2}}}\,\mathrm {d} t.}$

• An ellipse with a large semi-axis and a small semi-axis is parameterized by for . So your scope is ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle (a\cos t,\,b\sin t)}$ ${\displaystyle t\in [0,2\pi ]}$

${\displaystyle \int \limits _{0}^{2\pi }{\sqrt {a^{2}\sin ^{2}t+b^{2}\cos ^{2}t}}\,\mathrm {d} t=4a\int \limits _{0}^{\frac {\pi }{2}}{\sqrt {1-\varepsilon ^{2}\cos ^{2}t}}\;\mathrm {d} t}$.

The numerical eccentricity of the ellipse denotes . Because of this relationship, the integral on the right-hand side is called the elliptical integral . ${\displaystyle \varepsilon }$ ${\displaystyle {\sqrt {1-b^{2}/a^{2}}}}$

Path independence

If a vector field is a gradient field , i. H. is the gradient of a scalar field , with ${\displaystyle \mathbf {F} }$ ${\displaystyle \mathbf {F} }$ ${\displaystyle V}$

${\displaystyle \mathbf {\nabla } V=\mathbf {F} ,}$

so applies to the derivation of the concatenation of and ${\displaystyle V}$ ${\displaystyle \mathbf {r} (t)}$

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}}V(\mathbf {r} (t))=\mathbf {\nabla } V(\mathbf {r} (t))\cdot {\dot {\mathbf {r} }}(t)=\mathbf {F} (\mathbf {r} (t))\cdot {\dot {\mathbf {r} }}(t)}$

which corresponds to the integrand of the path integral over on . From this it follows for a given curve ${\displaystyle \mathbf {F} }$ ${\displaystyle \mathbf {r} (t)}$ ${\displaystyle {\mathcal {S}}}$

${\displaystyle \int \limits _{\mathcal {S}}\mathbf {F} (\mathbf {x} )\cdot \,\mathrm {d} \mathbf {x} =\int \limits _{a}^{b}\mathbf {F} (\mathbf {r} (t))\cdot {\dot {\mathbf {r} }}(t)\,\mathrm {d} t=\int \limits _{a}^{b}{\frac {\mathrm {d} }{\mathrm {d} t}}V(\mathbf {r} (t))\,\mathrm {d} t=V(\mathbf {r} (b))-V(\mathbf {r} (a)).}$

Any two curves and in a gradient field ${\displaystyle {\mathcal {S}}1}$ ${\displaystyle {\mathcal {S}}2}$

This means that the integral of over depends exclusively on the points and and the way between is irrelevant for the result. For this reason the integral of a gradient field is called "path-independent". ${\displaystyle \mathbf {F} }$ ${\displaystyle {\mathcal {S}}}$ ${\displaystyle \mathbf {r} (b)}$ ${\displaystyle \mathbf {r} (a)}$

In particular, applies to the ring integral over the closed curve , with any two paths and ${\displaystyle {\mathcal {S}}}$ ${\displaystyle {\mathcal {S}}_{1}}$ ${\displaystyle {\mathcal {S}}_{2}}$

${\displaystyle \oint \limits _{\mathcal {S}}\mathbf {F} (\mathbf {x} )\,\mathrm {d} \mathbf {x} =\int \limits _{1,{\mathcal {S}}_{1}}^{2}\mathbf {F} (\mathbf {x} )\,\mathrm {d} \mathbf {x} +\int \limits _{2,{\mathcal {S}}_{2}}^{1}\mathbf {F} (\mathbf {x} )\,\mathrm {d} \mathbf {x} =0}$

This is particularly important in physics , since gravity , for example, has these properties. Since the energy in these force fields is always a conserved quantity, they are called conservative force fields in physics . The scalar field is the potential or the potential energy . Conservative force fields preserve the mechanical energy, i.e. i. the sum of kinetic energy and potential energy. According to the above integral, a total of 0 J work is applied on a closed curve. ${\displaystyle V}$

Path independence can also be shown with the help of the integrability condition .

The curve circles the zero point twice. ${\displaystyle \gamma }$ ${\displaystyle z_{0}}$

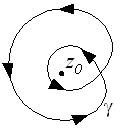
If the vector field can not be represented as a gradient field only in a (small) vicinity of a point, the closed path integral of curves outside of is proportional to the number of turns around this point and otherwise independent of the exact course of the curve (see Algebraic Topology: Methodology ). ${\displaystyle U}$ ${\displaystyle U}$

Complex path integrals

If a complex-valued function is called integrable, if and are integrable. One defines ${\displaystyle f\colon [a,b]\to \mathbb {C} }$ ${\displaystyle f}$ ${\displaystyle \operatorname {Re} f}$ ${\displaystyle \operatorname {Im} f}$

${\displaystyle \int \limits _{a}^{b}f(x)\mathrm {d} x:=\int \limits _{a}^{b}\operatorname {Re} f(x)\mathrm {d} x+\mathrm {i} \int \limits _{a}^{b}\operatorname {Im} f(x)\mathrm {d} x}$.

The integral is therefore -linear. Is continuous and an antiderivative of , then applies as in real ${\displaystyle \mathbb {C} }$ ${\displaystyle f}$ ${\displaystyle F}$ ${\displaystyle f}$

${\displaystyle \int \limits _{a}^{b}f(x)\mathrm {d} x=F(b)-F(a)}$.

The concept of integral is now extended to the complex level as follows: If a complex-valued function in a domain , and is a piecewise continuously differentiable path in , then the path integral of along the path is defined as ${\displaystyle f\colon U\to \mathbb {C} }$ ${\displaystyle U\subseteq \mathbb {C} }$ ${\displaystyle \gamma \colon [0,1]\to U}$ ${\displaystyle U}$ ${\displaystyle f}$ ${\displaystyle \gamma }$

${\displaystyle \int \limits _{\gamma }f:=\int \limits _{\gamma }f(z)\,\mathrm {d} z:=\int \limits _{0}^{1}f(\gamma (t))\cdot {\dot {\gamma }}(t)\,\mathrm {d} t.}$

The painting point here denotes complex multiplication.

The central statement about path integrals of complex functions is Cauchy's integral theorem : For a holomorphic function , the path integral only depends on the homotopy class of . If it is simply connected , the integral does not depend on , but only on the start and end point. ${\displaystyle f}$ ${\displaystyle \gamma }$ ${\displaystyle U}$ ${\displaystyle \gamma }$

Analogous to the real case, the length of the path is defined through ${\displaystyle \gamma }$

${\displaystyle \operatorname {L} (\gamma ):=\int \limits _{0}^{1}\left|{\dot {\gamma }}(t)\right|\mathrm {d} t}$.

The following inequality, the so-called standard estimate , is of particular interest for theoretical purposes :

${\displaystyle \left|\int _{\gamma }f(z)\,\mathrm {d} z\right|\leq \operatorname {L} (\gamma )\cdot C}$if applies to everyone . ${\displaystyle \left|f(z)\right|\leq C}$ ${\displaystyle z\in \gamma ([0,1])}$

As in the real case, the path integral is independent of the parameterization of the path , ie it is not absolutely necessary to choose the parameter range, as can be shown by substitution. This allows the definition of complex curve integrals by replacing the path in the above formulas with a curve in . ${\displaystyle \gamma }$ ${\displaystyle [0,1]}$ ${\displaystyle \gamma }$ ${\displaystyle {\mathcal {C}}}$ ${\displaystyle \mathbb {C} }$

See against it

• Path integral

literature

• Harro Heuser : Textbook of Analysis - Part 2 . 1981; 5th edition, Teubner 1990, ISBN 3-519-42222-0 , p. 369 sentence 180.1, p. 391 sentence 184.1, p. 393 sentence 185.1

Web links

Wiktionary: curve integral  - explanations of meanings, word origins, synonyms, translations

• Curve integrals in Matroids Matheplanet
• Curve integral at PlanetMath (English)

Individual evidence

1. ^ Klaus Knothe, Heribert Wessels: Finite elements . An introduction for engineers. 3. Edition. 1999, ISBN 978-3-540-64491-0 , pp. 524 .