Image (math)
In a mathematical function that is image, the image set and the image area of a subset of the defined range , the amount of values from the target quantity , the on takes actually.
The words set of values or range of values are often used for this purpose, but other authors use these to denote the entire target set .
definition
Most common notation
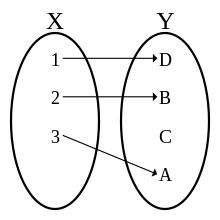
For a function and a subset of , the following set is called the image of M under f:
The image of f is then the image of the definition set under , thus:
In general, the usual set notation is used to represent the image set, in the example above:
Alternative notations
- The notation is also used for to indicate that it is not to be applied to the whole, but to the members of this set as an element. Occasionally occurs as a further notation .
- The English name ("im" from the English word image ) is also used for.
Examples
We consider the function ( whole numbers ) with .
- Different sets of input are not necessarily sent to different sets of images:
- Overall, the set of square numbers is the picture of the function:
properties
Let it be a function and and be subsets of :
- is surjective if and only if .
-
If injective , then equality also applies here.
The statements about union and intersection can be generalized from two subsets to any non-empty families of subsets.
See also
Individual evidence
- ↑ a b Harro Heuser : Textbook of Analysis. Part 1. 8th, revised edition. BG Teubner, Stuttgart 1990, ISBN 3-519-12231-6 , p. 106.
- ↑ Reinhard Dobbener: Analysis. Study book for economists. 4th, corrected edition. Oldenbourg Wissenschaftsverlag, Munich a. a. 2007, ISBN 978-3-486-57999-4 , p. 12, definition 1.12.
- ↑ Michael Ruzicka, Lars Diening: Analysis I. course of the winter semester 2004/2005. ( Memento from January 23, 2005 in the Internet Archive ). P. 21. ( Memento of October 21, 2013 in the Internet Archive ) (PDF; 74 kB).
- ^ Jean E. Rubin: Set Theory for the Mathematician . Holden-Day, 1967, p. xix .
- ↑ M. Randall Holmes: Inhomogeneity of the urelements in the usual models of NFU. December 29, 2005, on: Semantic Scholar. P. 2.









![f [M]](https://wikimedia.org/api/rest_v1/media/math/render/svg/da22846ca5b315395b2541cc80646b450e7cb7f4)














