Subset

The mathematical terms subset and superset describe a relationship between two sets . Another word for subset is subset .
For the mathematical representation of the embedding of a subset to its basic amount mathematical function of the subset relationship that is inclusion mapping used. is a subset of and is a superset of if every element of is also contained in. If also contains further elements that are not contained in, then is a true subset of and is a true superset of . The set of all subsets of a given set is called the power set of .
Georg Cantor - the "inventor" of set theory - coined the term subset from 1884; the symbol of the subset relation was introduced by Ernst Schröder in 1890 in his " Algebra of Logic ".
definition
If and are sets and every element of is also an element of , one calls a subset or subset of :
Conversely, the superset of is called if and only if is a subset of :
There is also the concept of the real subset. is a proper subset of if and only if a subset of and is not identical to .
Again you write when .
Further notations
Some authors also use the characters and for subset and superset instead of and . Most of the time, the author does not define the term “real subset”.
Other authors prefer the characters and instead of and for proper subset and superset . This usage is fittingly reminiscent of the signs of inequality and . Since this notation is mostly used when the difference between real and non-real subset is important, the characters and are rarely used.
Variants of the character are also , and . If is not a subset of , can also be used. Corresponding spellings are for , and for , as well as (no superset).
The corresponding Unicode symbols are: ⊂, ⊃, ⊆, ⊇, ⊄, ⊅, ⊈, ⊉, ⊊, ⊋ (see: Unicode Block Mathematical Operators ).
Ways of speaking
Instead of “ is a subset of .”, “The amount is contained in the amount ” or “The amount is comprised of .” Is also used . In the same way, instead of “ is a superset of .”, “The set contains the set .” Or “The set includes the set .” Is also used. If there cannot be misunderstandings, “ contains ” etc. is also said. Misunderstandings can arise especially with "The quantity contains the element ."
Examples
- {1, 2} is a (real) subset of {1, 2, 3}.
- {1, 2, 3} is a (spurious) subset of {1, 2, 3}.
- {1, 2, 3, 4} is not a subset of {1, 2, 3}.
- {1, 2, 3} is not a subset of {2, 3, 4}.
- {} is a (real) subset of {1, 2}.
- {1, 2, 3} is a (proper) superset of {1, 2}.
- {1, 2} is an (improper) superset of {1, 2}.
- {1} is not a superset of {1, 2}.
- The set of prime numbers is a real subset of the set of natural numbers .
- The set of rational numbers is a proper subset of the set of real numbers .
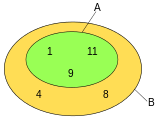
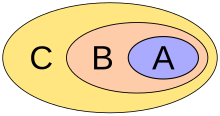
Further examples as quantity diagrams:
properties
- The empty set is a subset of every set:
- Every set is a subset of itself:
- Characterization of inclusion with the help of the association :
- Characterization of inclusion using the average :
- Characterization of inclusion using the difference set :
- Characterization of inclusion using the characteristic function :
- Two sets are equal if and only if each is a subset of the other:
- This rule is often used in proving the equality of two sets by showing mutual inclusion (in two steps).
- When transitioning to complement , the direction of inclusion reverses:
- When forming the intersection, you always get a subset:
- When forming the union one always gets a superset:
Inclusion as an order relation
Inclusion as a relation between sets fulfills the three properties of a partial order relation , namely it is reflexive , antisymmetric and transitive :
(This is an abbreviation for and .)
So if there is a set of sets (a set system ), then there is a partial order . This is especially true for the power set of a given set .
Chains of inclusion
If a system of quantities is such that two of the quantities occurring in one encompass the other or are encompassed by the other, then such a system of quantities is called an inclusion chain . An example of this is provided by the system of left-hand unrestricted open intervals of .
A special case of an inclusion chain is when a (finite or infinite) sequence of quantities is given, which is arranged in ascending or descending order. You then write briefly:
Size and number of subsets
- Every subset of a finite set is finite and the following applies to the cardinalities :
- Every superset of an infinite set is infinite.
- Even with infinite quantities, the following applies to the thicknesses:
- In the case of infinite sets, however, it is possible that a real subset has the same cardinality as its basic set. For example, the natural numbers are a true subset of the whole numbers , but the two sets are equally powerful (namely, countably infinite ).
- After Cantor's theorem is the power set of a quantity always more powerful than the amount itself: .
- A finite set with elements has exactly subsets.
- The number of -element subsets of a -element (finite) set is given by the binomial coefficient .
See also
literature
- Oliver Deiser: Introduction to set theory . Springer, 2004, ISBN 978-3-540-20401-5
- John L. Kelley: General Topology . Springer-Verlag, Berlin / Heidelberg / New York 1975, ISBN 3-540-90125-6 (reprint of the edition by Van Nostrand from 1955).
Web links
Individual evidence
- ↑ a b Oliver Deiser: Introduction to set theory . Springer, 2004, ISBN 978-3-540-20401-5 , p. 33 ( excerpt (Google) ).
- ↑ Adolf Fraenkel: Introduction to set theory: An elementary introduction to the realm of the infinitely great . Springer, 2nd edition, 2013, ISBN 9783662259009 , p. 15
- ↑ Set theory . In: Encyclopedia of Mathematics .
- ↑ Otto Kerner, Joseph Maurer, Jutta Steffens, Thomas Thode, Rudolf Voller: Vieweg Mathematik Lexikon . Vieweg, 1988, ISBN 3-528-06308-4 , p. 190.












































![\ {{] {- \ infty, x} [} \ mid x \ in \ R \}](https://wikimedia.org/api/rest_v1/media/math/render/svg/859ccfd71aa073323c9c536313a7e253b1cd8178)









