Reflexive relation
The reflexivity of a two-digit relation on a set is given if applies to all elements of the set, i.e. every element is related to itself. It is then called reflexive .
A relation is called non-reflexive if the relation does not apply to any element of the set, i.e. no element is related to itself. There are also relations which are neither reflexive nor irreflexive if the relation holds for some elements of the set, but not for all.
Reflexivity is one of the prerequisites for an equivalence relation or an order relation ; Irreflexibility is one of the prerequisites for a strict order relation .
Formal definition
If there is a set and a two-digit relation , then one defines (using the infix notation ):
- is reflexive :
- is irreflexive :
Examples
Reflexive
- The less than or equal relation on the real numbers is reflexive because it always holds. It is also a total order . The same applies to the relation .
- The usual equality on the real numbers is reflexive, since it always holds. It is also an equivalence relation .
- The subset relationship between sets is reflexive, since it always holds. It is also a partial order .
Irreflective
- The less than relation on the real numbers is irreflexive because it never holds. It is also a strict total order . The same applies to the relation .
- The inequality on the real numbers is non- reflective because it never holds.
- The real subset relationship between sets is irreflexible because it never holds. It is also a strict partial order .
Neither reflexive nor irreflexive
The following relation on the set of real numbers is neither reflexive nor irreflexive:
Reason: For applies , for applies .
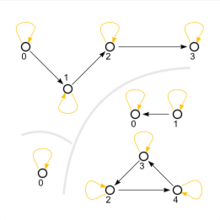
Representation as a directed graph
Any relation on a set can be viewed as a directed graph (see example in the picture above). The nodes of the graph are the elements of . A directed edge (an arrow ) is drawn from node to node if and only if applies.
The reflexivity of can now be characterized in the graph as follows: There is a loop for every node . Correspondingly, the irreflectivity is given by the fact that there is no loop for any node .
properties
- With the help of the identical relation (which consists of all pairs ) one can also characterize the terms as follows:
- is reflexive
- is irreflexive
- If the relation is reflexive or irreflexive, then this also applies to the converse relation . Examples: the relation is too converse, the relation is too converse .
- If the relation is reflexive, then the complementary relation is irreflexive. If it is irreflexive, then it is reflexive. The complementary relation is defined by
- .
- The relation on the empty set is the only relation both reflexive and irreflexive.




































