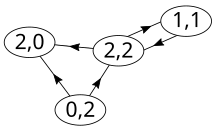
Directed graph

A directed graph with 3 nodes and 4 directed edges (double arrow corresponds to two arrows running in opposite directions)

A directed graph or digraph (from English directed graph ) consists of

• a set of nodes ( English vertex / vertices , often also called corners ) and ${\displaystyle V}$
• a set of ordered vertex pairs of edges . ${\displaystyle E\subseteq V\times V}$

The edges of a directed graph are directed edges ( English directed edge / edges , sometimes arcs ). These are often shown as arrows and can only be traversed in one direction. In contrast, the edges of an undirected graph are unordered pairs of nodes . Directed graphs are used to represent objects and the connections between them, for example of finite automata . ${\displaystyle (v,w)\in E}$ ${\displaystyle \{v,w\}}$

Basic concepts

A directed graph without multiple edges and loops is called a simple digraph (also known as a simple digraph ).

It is said that a directed edge goes from to . It is the walk (or start node ) and the head (or end nodes ) from . Furthermore is considered the direct successor of and as the direct predecessor of . If there is a path in a graph from to , a successor to and a predecessor of is considered . The edge is called the flipped or inverted edge of . ${\displaystyle e=(x,y)}$ ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle e}$ ${\displaystyle y}$ ${\displaystyle x}$ ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle y}$ ${\displaystyle x}$ ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle (y,x)}$ ${\displaystyle (x,y)}$

A directed graph is called symmetric if every edge also contains the corresponding inverted edge. An undirected graph can easily be converted to a symmetric directed graph by replacing each edge with the two directed edges and . ${\displaystyle G}$ ${\displaystyle G}$ ${\displaystyle \{x,y\}}$ ${\displaystyle (x,y)}$ ${\displaystyle (y,x)}$

To get an orientation of a simple undirected graph , each edge has to be assigned a direction. Any directed graph constructed in this way is called an oriented graph . In contrast to the oriented graph, a simply directed graph may contain edges in both directions between two nodes.

A weighted digraph is a digraph whose edges are assigned weights, resulting in an edge-weighted graph . A digraph with weighted edges is called a network in graph theory .

The adjacency matrix of a digraph (with loops and multiple edges) is an integer matrix whose rows and columns correspond to the nodes of the digraph. An entry outside the main diagonal indicates the number of edges from node to node , and the entry of the main diagonal corresponds to the number of loops in the node . The adjacency matrix of a digraph is unambiguous except for the interchanging of rows and columns. ${\displaystyle a_{ij}}$ ${\displaystyle i}$ ${\displaystyle j}$ ${\displaystyle a_{ii}}$ ${\displaystyle i}$

A digraph can also be represented by an incidence matrix .

Related directed graphs

→ Main article : Relationship (graph theory)

A directed graph is called weakly connected (or only connected ) if the underlying graph of , which is obtained by replacing all directed edges with undirected ones, is a connected graph. A directed graph is called strongly connected or strongly if two of its nodes are mutually accessible. A maximal strongly connected subgraph of is a strong component . ${\displaystyle G}$ ${\displaystyle G}$ ${\displaystyle G}$

Ingress and egress degrees

Digraph with nodal labeling (degree of entry and exit).

→ Main article : "Directed graphs" in the article Degree (graph theory)

The number of direct predecessor of a node is in-degree (also internal degrees ) and the number of direct successors output level (or exterior grade called).

The entrance degree of a node in a graph is denoted by and the external degree by . A node with is called a source and a node with is called a sink . A sink is called a universal sink if it has incoming edges from every other node, i.e. if its degree of input is the same . ${\displaystyle v}$ ${\displaystyle G}$ ${\displaystyle d_{G}^{-}(v)}$ ${\displaystyle d_{G}^{+}(v)}$ ${\displaystyle d_{G}^{-}(v)=0}$ ${\displaystyle d_{G}^{+}(v)=0}$ ${\displaystyle |V|-1}$

For directed graphs, the sum of all input degrees is equal to the sum of all output degrees, and both are equal to the sum of the directed edges:

${\displaystyle \sum _{v\in V}d_{G}^{+}(v)=\sum _{v\in V}d_{G}^{-}(v)=|E|\,.}$

If the equation holds for all nodes , the graph is called a balanced digraph . ${\displaystyle v\in V}$ ${\displaystyle d_{G}^{+}(v)=d_{G}^{-}(v)}$

Representation of directed graphs

The directed graph treated in the example

In addition to the naive display of a directed graph by specifying the number of nodes and edges, there are other display options, the so-called edges or node field.

Edge field

An edge field is a type of representation for directed graphs according to the following scheme:

${\displaystyle |V|,|E|,E_{1},\ldots ,E_{|E|}}$,

where the number of nodes, the number of edges and the edges are with . ${\displaystyle |V|}$ ${\displaystyle |E|}$ ${\displaystyle E_{1},\ldots ,E_{|E|}}$ ${\displaystyle E_{i}=(v,w)\in E}$

Node field

A node field is a type of representation for directed graphs with the following structure:

${\displaystyle |V|,|E|,{\text{ag}}(V_{1}),{\text{Ziel}}_{1},\ldots ,{\text{Ziel}}_{{\text{ag}}(V_{1})},\ldots ,{\text{ag}}(V_{|V|}),{\text{Ziel}}_{1},\ldots ,{\text{Ziel}}_{{\text{ag}}(V_{|V|})}}$,

where is the number of nodes, the number of edges and the exit degree of the node . ${\displaystyle |V|}$ ${\displaystyle |E|}$ ${\displaystyle ag(V)}$ ${\displaystyle V}$

example

If one looks at the directed graph on the right as an example, then is the edge field and the node field . The numbers in bold indicate the degree of exit. ${\displaystyle 4,6,(1,2),(1,4),(2,4),(3,1),(3,2),(4,3)}$ ${\displaystyle 4,6,\mathbf {2} ,2,4,\mathbf {1} ,4,\mathbf {2} ,1,2,\mathbf {1} ,3}$

Classes of directed graphs

Simply directed acyclic graph

Tournament graph with 4 nodes

Symmetrically directed graphs are directed graphs in which all edges are bidirectional, ie for each edge that belongs to the graph , the corresponding reverse edge also belongs to it.

Simple directed graphs are directed graphs without loops and without multiple edges.

Complete directed graphs are simple directed graphs in which each pair of nodes is connected by a symmetrical pair of directed edges. This corresponds to an undirected complete graph whose edges are replaced by pairs of directed edges. It follows that a completely directed graph is symmetric.

Oriented graphs are directed graphs without bidirectional edges. It follows that a directed graph is an oriented graph if and only if it does not have a 2-cycle.

Tournament graphs are oriented graphs obtained by choosing a direction for each edge in undirected complete graphs.

A directed acyclic graph or acyclic digraph is a directed graph that does not contain a directed circle . Special cases of directed acyclic graphs are multiple trees (two directed paths of the graph that start from the same start node must not meet in the same end node), oriented trees or poly trees (orientation of an undirected acyclic graph) and root trees (oriented trees with all edges of the underlying undirected tree away from the root node).

Weighted directed graphs or directed networks are simple directed graphs with weights assigned to their edges , similar to weighted graphs, also known as undirected networks or weighted networks.

Flow networks are weighted directed graphs with two special nodes , the source and the sink .

Control flow graphs are directed graphs that are used in computer science to represent the paths that can be followed during the execution of a computer program.

Signal flow graphs are weighted directed graphs in which nodes represent system variables and edges represent functional connections between pairs of nodes.

State transition diagrams are directed multigraphs that represent finite automata .

Commutative diagrams are directed graphs used in category theory, where the nodes represent mathematical objects and the edges mathematical functions , with the property that all directed paths with the same start and end nodelead to the same resultby composition .

Combinatorics

The number of simple directed graphs with nodes increases rapidly with the number of nodes and is the same . So it increases exponentially to the number of edges of the complete graph . If the nodes are not numbered, i.e. isomorphic graphs are not counted, this number is roughly proportional to , because for most isomorphism classes all graphs that result from the permutation of the numbered nodes are different. The following table shows the numbers determined with the help of a computer for : ${\displaystyle n}$ ${\displaystyle 4^{\tfrac {n\cdot (n-1)}{2}}}$ ${\displaystyle {\tfrac {n\cdot (n-1)}{2}}}$ ${\displaystyle K_{n}}$ ${\displaystyle {\tfrac {1}{n!}}\cdot 4^{\tfrac {n\cdot (n-1)}{2}}}$ ${\displaystyle n!}$ ${\displaystyle n\leq 8}$

Number of directed graphs without numbered nodes
n	all	coherent	strongly coherent
1	1	1	1
2	3	2	1
3	16	13	5
4th	218	199	83
5	9608	9364	5048
6th	1540944	1530843	1047008
7th	882033440	880471142	705422362
8th	1793359192848	1792473955306	1580348371788

See also

• Kautz graph

literature

• Jørgen Bang-Jensen, Gregory Gutin: Digraphs: Theory, Algorithms and Applications . Springer, 2000, ISBN 1-85233-268-9 ( rhul.ac.uk ).
• John Adrian Bondy, USR Murty: Graph Theory with Applications . North-Holland, 1976, ISBN 0-444-19451-7 .
• Reinhard Diestel: Graph Theory . 3. Edition. Springer, 2005, ISBN 3-540-26182-6 .
• Frank Harary, Robert Z. Norman, Dorwin Cartwright: Structural Models: An Introduction to the Theory of Directed Graphs . Wiley, New York 1965.

Individual evidence

1. ↑ ^{a b} Reinhard Diestel : Graph theory . 4th edition. Springer, Berlin a. a. 2010, ISBN 978-3-642-14911-5 , pp. 28–30 (English, 4th electronic edition 2010 - first edition: 1996).
2. ↑ Volker Turau: Algorithmic Graph Theory . 3. Edition. Oldenbourg Wissenschaftsverlag, Munich 2009, ISBN 978-3-486-59057-9 , p. 20-24 .
3. ↑ Eric W. Weisstein : Oriented Graph . In: MathWorld (English).
4. ↑ Eric W. Weisstein : Graph Orientation . In: MathWorld (English).
5. ↑ Reinhard Diestel : Graph theory . 4th edition. Springer, Berlin a. a. 2010, ISBN 978-3-642-14911-5 , pp. 145–168 (English, 4th electronic edition 2010 - first edition: 1996).
6. ^ Bang-Jensen, Gutin: Digraphs: Theory, Algorithms and Applications, 2nd edition, 2009, p. 20.
7. ↑ Bhavanari Satyanarayana, Kuncham Syam Prasad: Discrete Mathematics and Graph Theory . PHI Learning Pvt. Ltd., 2009, ISBN 978-81-203-3842-5 , pp. 460 .
8. ^ Richard A. Brualdi: Combinatorial matrix classes . In: Encyclopedia of mathematics and its applications . tape 108 . Cambridge University Press, 2006, ISBN 978-0-521-86565-4 , pp. 51 .
9. ↑ Follow A000088 in OEIS
10. ↑ Follow A000088 in OEIS
11. ↑ Follow A035512 in OEIS