Matrix (math)
In mathematics , a matrix (plural matrices ) is a rectangular arrangement (table) of elements (mostly mathematical objects , such as numbers). You can then calculate with these objects in a certain way by adding matrices or multiplying them with one another.
Matrices are a key concept in linear algebra and appear in almost all areas of mathematics. They clearly show relationships in which linear combinations play a role and thus facilitate arithmetic and thought processes. They are used in particular to represent linear images and to describe and solve linear systems of equations . The name matrix was introduced in 1850 by James Joseph Sylvester .
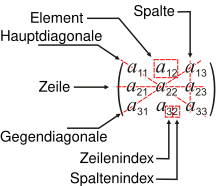
The elements are arranged in rows and columns , as shown in the figure below . The generalization to more than two indices is also called a hypermatrix .
Concepts and first properties
notation
The arrangement of the elements in rows and columns between two large opening and closing brackets has established itself as a notation. As a rule, round brackets are used, but square brackets are also used. For example denote
- and
Matrices with two rows and three columns. Matrices are usually designated with capital letters (sometimes in bold or, handwritten, single or double underlined), preferably . A matrix with rows and columns:
- .
Elements of the matrix
The elements of the matrix are also called entries or components of the matrix. They come from a set , usually a body or a ring . One speaks of a matrix about . If one chooses for the set of real numbers , one speaks of a real matrix, in the case of complex numbers of a complex matrix.
A certain element is described by two indices , usually the element in the first row and the first column is described by. Generally denotes the element in the -th row and -th column. When indexing, the row index is always mentioned first and the column index of the element second. Remember rule: line first, column later. If there is a risk of confusion, the two indices are separated with a comma. For example, the matrix element in the first row and the eleventh column is denoted by.
Individual rows and columns are often referred to as column or row vectors . An example:
- here are and the columns or column vectors as well as and the rows or row vectors.
In the case of single row and column vectors in a matrix, the unchangeable index is sometimes left out. Sometimes column vectors are written as transposed row vectors for a more compact representation, so:
- or as or
Type
The type of a matrix results from the number of its rows and columns. A matrix with rows and columns is called a matrix (read: m-by-n - or m-cross-n matrix ). If the number of rows and columns match, one speaks of a square matrix.
A matrix that consists of only one column or only one row is usually understood as a vector . A vector with elements can be represented as a single-column matrix or a single- row matrix, depending on the context . In addition to the terms column vector and row vector, the terms column matrix and row matrix are also used. A matrix is both column and row matrix and is considered a scalar .
Formal representation
A matrix is a double-indexed family . Formally, this is a function
which assigns the entry to each index pair as a function value. For example, the entry is assigned to the index pair as a function value. The function value is therefore the entry in the -th row and -th column. The variables and correspond to the number of rows or columns. Not to be confused with this formal definition of a matrix as a function is that matrices themselves describe linear mappings .
The set of all matrices over the set is also written in common mathematical notation ; the short notation has become established for this. Sometimes the spellings or are used less often.
Addition and multiplication
Elementary arithmetic operations are defined in the space of the matrices.
Matrix addition
Two matrices can be added if they are of the same type, that is, if they have the same number of rows and the same number of columns. The sum of two matrices is defined by component:
Sample calculation:
In linear algebra, the entries of the matrices are usually elements of a field , e.g. B. the real or complex numbers . In this case the matrix addition is associative , commutative and has a neutral element with the zero matrix . In general, matrix addition only has these properties if the entries are elements of an algebraic structure that has these properties.
Scalar multiplication
A matrix is multiplied by a scalar by multiplying each entry in the matrix by the scalar:
Sample calculation:
The scalar multiplication must not be confused with the scalar product . In order to be able to perform the scalar multiplication, the scalar ( lambda ) and the entries in the matrix must come from the same ring . The set of matrices in this case is a (left) module over
Matrix multiplication
Two matrices can be multiplied if the number of columns in the left matrix corresponds to the number of rows in the right matrix. The product of a matrix and a matrix is a matrix whose entries are calculated by applying the sum of products formula, similar to the scalar product, to pairs of a row vector of the first matrix and a column vector of the second matrix:
The matrix multiplication is not commutative ; i.e., in general . The matrix multiplication is, however, associative ; i.e., it always applies:
A chain of matrix multiplications can therefore be bracketed in different ways. The problem of finding a bracket that leads to a calculation with the minimum number of elementary arithmetic operations is an optimization problem . The matrix addition and matrix multiplication also satisfy the two distributive laws :
for all matrices and matrices as well
for all matrices and matrices
Square matrices can be multiplied by themselves, analogous to the power of the real numbers, the matrix power or etc. are abbreviated . It makes sense to use square matrices as elements in polynomials. For more information on this, see Characteristic Polynomial . The Jordanian normal form can be used here for easier calculation . Square matrices above or beyond that can even be used in power series, cf. Matrix exponential . The square matrices over a ring , that is, play a special role with regard to matrix multiplication . With the matrix addition and multiplication, these in turn form a ring, which is called the matrix ring .
Further arithmetic operations
Transposed matrix
The transpose of a matrix is the matrix , that is, to
is
the transpose. So you write the first row as the first column, the second row as the second column, etc. The matrix is mirrored on its main diagonal . The following calculation rules apply:
For matrices above the adjoint matrix is exactly the transposed matrix.
Inverse matrix
If the determinant of a square matrix over a body is not equal to zero, i.e. i.e., if so, the matrix inverse to the matrix exists . For this applies
- ,
where the - is identity matrix . Matrices that have an inverse matrix are called invertible or regular matrices . These have full rank . Conversely, non-invertible matrices are called singular matrices. A generalization of the inverse for singular matrices are so-called pseudo-inverse matrices.
Vector vector products
The matrix product of two -Vectors and is not defined because the number of columns of is generally not equal to the number of rows of . The two products and do exist, however.
The first product is a matrix that is interpreted as a number; it is called the standard scalar product of and and is denoted by or . Geometric that dot product corresponds to a Cartesian coordinate system the product
the magnitudes of the two vectors and the cosine of the angle enclosed by the two vectors. For example
The second product is a matrix and is called the dyadic product or tensor product of and (written ). Its columns are scalar multiples of , its rows are scalar multiples of . For example
Vector spaces of matrices
The set of -matrices over a field forms with the matrix addition and the scalar multiplication a - vector space . This vector space has the dimension . A base of is given by the amount of the standard dies with , . This base is sometimes referred to as the standard base of .
The trace of the matrix product
is then in the special case a real scalar product . In this Euclidean vector space , the symmetrical matrices and the skew-symmetrical matrices are perpendicular to one another. If there is a symmetric and a skew-symmetric matrix, then we have .
In the special case is the trace of the matrix product
becomes a complex scalar product and the matrix space becomes a unitary vector space . This scalar product is also called the Frobenius scalar product . The norm induced by the Frobenius scalar product is called the Frobenius norm and with it the matrix space becomes a Banach space .
Applications
Relationship with linear maps
The special thing about matrices over a ring is the connection to linear maps . A linear mapping with a definition range (set of column vectors) and value range can be defined for each matrix by mapping each column vector to . Conversely, each linear mapping corresponds exactly to one matrix in this way ; where the columns from are the images of the standard basis vectors from below . This relationship between linear mappings and matrices is also known as (canonical) isomorphism
Given a given and, it represents a bijection between the set of matrices and the set of linear images. The matrix product is transformed into the composition (sequential execution) of linear images. Because the brackets play no role in the execution of three linear mappings one after the other, this also applies to the matrix multiplication, which is therefore associative .
If there is even a body, one can consider arbitrary finite-dimensional vector spaces and (of dimension or ) instead of the column vector spaces . (If a commutative ring with 1, then one can analog-free K-modules to view.) These are the choice of bases of , and of the coordinate spaces or isomorphic, because at any given vector a unique decomposition into basis vectors
exists and the body elements occurring in it the coordinate vector
form. However, the coordinate vector depends on the base used , which is also included in the name .
The situation is analogous in vector space. If a linear mapping is given, the images of the basis vectors of can be uniquely divided into the basis vectors of in the form
with coordinate vector
The mapping is then completely defined by the so-called mapping matrix
because for the picture of the above Vector applies
thus ("coordinate vector = matrix times coordinate vector"). (The matrix depends on the bases used and ; with multiplication, the base that is to the left and right of the painting point is “truncated” and the “outside” base is left over.)
The execution of two linear mappings and (with bases , or ) one after the other corresponds to the matrix multiplication, i.e.
(Here, too, the base is "shortened").
Thus, the set of linear mappings from to is again isomorphic to. The isomorphism depends on the selected bases and from and is therefore not canonical: If you choose a different basis for or for , the same linear map is assigned a different matrix from the old is created by multiplying right or left with an invertible matrix or matrix (so-called base change matrix ) that only depends on the bases involved . This follows by applying the multiplication rule from the previous paragraph twice, namely
("Matrix = base change matrix times matrix times base change matrix"). The identity mappings and each vector form from or onto themselves.
If a property of matrices remains unaffected by such base changes, it makes sense to assign this property to the corresponding linear mapping regardless of the base.
Terms that are often used in connection with matrices are the rank and the determinant of a matrix. The rank is (if there is a body) in the stated sense independent of the base, and one can therefore speak of the rank also for linear mappings. The determinant is only defined for square matrices that match the case ; it remains unchanged if the same base change is carried out in the definition and value range, with both base change matrices being inverse to one another:
In this sense, the determinant is also independent of the base.
Transformation of matrix equations
Especially in the multivariate method arguments, derivations are often so in matrices calculus performed.
In principle, equations are transformed like algebraic equations, although the non-commutativity of matrix multiplication and the existence of zero divisors must be taken into account.
Example: Linear system of equations as a simple transformation
Find the solution vector of a linear system of equations
with as coefficient matrix. If the inverse matrix exists, you can multiply with it from the left:
and you get the solution
Special matrices
Properties of endomorphisms
The following properties of square matrices correspond to properties of the endomorphisms they represent.
- Orthogonal matrices
- A real matrix is orthogonal if the associated linear map receives the standard scalar product, that is, if
- applies. This condition is equivalent to that the equation
- or.
- Fulfills.
- These matrices represent reflections, rotations and rotations.
- Unitary matrices
- They are the complex counterpart to the orthogonal matrices. A complex matrix is unitary if the associated transformation receives the normalization, that is, if
- applies. This condition is equivalent to that the equation
- Fulfills; the conjugate-transposed matrix denotes to
- If one understands the -dimensional complex vector space as -dimensional real vector space, then the unitary matrices correspond exactly to those orthogonal matrices that swap with the multiplication with .
- Projection matrices
- A matrix is a projection matrix, if
- holds, i.e. it is idempotent , that is, the multiple application of a projection matrix to a vector leaves the result unchanged. An idempotent matrix does not have a full rank unless it is the identity matrix. Geometrically, projection matrices correspond to the parallel projection along the null space of the matrix. If the null space is perpendicular to the image space , an orthogonal projection is obtained .
-
Example: Let it be a matrix and therefore not invertible itself. If the rank of is equal , then is invertible and so is the matrix
- idempotent. This matrix is used, for example, in the least squares method.
- Nilpotent matrices
- A matrix is called nilpotent if a power (and thus every higher power) results in the zero matrix.
Properties of bilinear shapes
Properties of matrices are listed below, the properties of the associated bilinear form
correspond. Nevertheless, these properties can also have an independent meaning for the endomorphisms shown.
- Symmetrical matrices
- A matrix is called symmetric if it is equal to its transposed matrix:
- In clear terms, the entries of symmetrical matrices are symmetrical to the main diagonal.
- Example:
- On the one hand, symmetric matrices correspond to symmetric bilinear forms:
- on the other hand the self-adjoint linear mappings:
- Hermitian matrices
- Hermitian matrices are the complex analog of symmetric matrices. They correspond to the Hermitian sesquilinear forms and the self-adjoint endomorphisms .
- A matrix is Hermitian or self-adjoint if:
- Misaligned matrices
- A matrix is called skew symmetric or also antisymmetric if the following applies:
- To meet this requirement, all entries on the main diagonal must have the value zero; the remaining values are mirrored on the main diagonal and multiplied by.
- Example:
- Skew-symmetric matrices correspond to antisymmetric bilinear forms:
- and anti-self-adjoint endomorphisms:
- Positive definite matrices
- A real matrix is positive definite if the associated bilinear form is positive definite, that is, if the following applies for all vectors :
- Positive definite matrices define generalized scalar products . If the bilinear form has no negative values, the matrix is called positive semidefinite. Similarly, a matrix can be called negative definite or negative semidefinite if the above bilinear form only has negative or no positive values. Matrices that do not meet any of these properties are called indefinite.
Other constructions
If a matrix contains complex numbers, the conjugate matrix is obtained by replacing its components with the conjugate complex elements. The adjoint matrix (also Hermitian conjugate matrix) of a matrix is denoted by and corresponds to the transposed matrix, in which all elements are also complexly conjugated.
- Adjoint or complementary matrix
The complementary matrix of a square matrix is made up of its sub-determinants, whereby one sub-determinant is also called a minor. To determine the sub-determinants , the -th row and -th column of are deleted. The determinant is then calculated from the resulting matrix . The complementary matrix then has the entries This matrix is sometimes also referred to as the matrix of cofactors .
- The complementary matrix is used, for example, to calculate the inverse of a matrix , because according to Laplace's expansion theorem:
- So the inverse is if
A transition or stochastic matrix is a matrix whose entries are all between 0 and 1 and whose rows or column sums result in 1. In stochastics they serve to characterize temporally discrete Markov chains with finite state space. The double-stochastic matrices are a special case of this .
Infinite dimensional spaces
Also for infinitely dimensional vector spaces (even over oblique bodies ) it applies that every linear mapping is uniquely determined by the images of the elements of a base and these can be chosen arbitrarily and can be continued to a linear mapping on completely . If now is a basis of , then one can clearly write as a (finite) linear combination of basis vectors, i. That is, there are unique coefficients for , of which only finitely many are different from zero, so that . Accordingly, every linear mapping can be understood as a possibly infinite matrix, but in every column ( "number" the columns and the column to consist of the elements of numbered coordinates ) only finitely many entries differ from zero, and vice versa. The correspondingly defined matrix multiplication in turn corresponds to the composition of linear images.
In functional analysis , one considers topological vector spaces , i. H. Vector spaces on which one can speak of convergence and accordingly also form infinite sums . In such cases, matrices with an infinite number of non-zero entries in a column can, under certain circumstances, be understood as linear mappings, whereby other basic terms are also used.
Hilbert spaces are a special case . So let Hilbert spaces and orthonormal bases of or . Then a matrix representation of a linear operator is obtained (for only densely defined operators it works as well if the domain has an orthonormal basis, which is always the case in the countable-dimensional case) by defining the matrix elements ; here is the scalar product in the Hilbert space under consideration (in the complex case semilinear in the first argument).
This so-called Hilbert-Schmidt scalar product can only be defined in the infinite-dimensional case for a certain subclass of linear operators, the so-called Hilbert-Schmidt operators , for which the series over which this scalar product is defined always converges.
literature
- Gerd Fischer : Linear Algebra. (An introduction for first-year students). 13th revised edition. Vieweg, Braunschweig et al. 2002, ISBN 3-528-97217-3 .
- Günter Gramlich: Linear Algebra. Fachbuchverlag Leipzig in Carl Hanser Verlag, Munich et al. 2003, ISBN 3-446-22122-0 .
- Klaus Jänich : Linear Algebra. 11th edition. Springer, Berlin et al. 2008, ISBN 978-3-540-75501-2 .
- Karsten Schmidt, Götz Trenkler: Introduction to Modern Matrix Algebra. With applications in statistics. 2nd, completely revised edition. Springer, Berlin et al. 2006, ISBN 3-540-33007-0 .
- Gilbert Strang : Linear Algebra. Springer, Berlin et al. 2003, ISBN 3-540-43949-8 .
Web links
- Matrix calculator - calculator that performs arithmetic operations for matrices with concrete numerical values, but also with variables.
- The Matrix Cookbook - An extensive matrix formulary collection in English (PDF; 522 kB).
supporting documents
- ↑ Eric W. Weisstein : Hypermatrix . In: MathWorld (English).