Least squares method
The method of least squares (short MKQ or English method of least squares , or only squares least briefly: LS . To delimit derived from extensions such as the generalized least squares method , or the two-stage least squares method also called "ordinary" with the addition, that ordinary least squares ( english ordinary least squares , in short: OLS )), or KQ method (deprecated method of least deviation sum of squares ) is the mathematical standard procedures for Adjustment . In this case, to a set of data points a function , determines the runs as close as possible to the data points and thus the best possible summarizing the data. The most frequently used function is the straight line , which then fit line is called. To be able to use the method, the function must contain at least one parameter . These parameters are then determined by the method so that when the function is compared with the data points and the distance between the function value and the data point is squared, the sum of these squared distances is as small as possible. The distances are then called residuals .
Typically, this method is used to examine real data, such as physical or economic measured values . These data often contain unavoidable measurement errors and fluctuations . With the assumption that the measured values are close to the underlying " true values " and that there is a certain relationship between the measured values, the method can be used to find a function that describes this relationship of the data as well as possible. The method can also be used in reverse to test different functions and thereby describe an unknown relationship in the data.

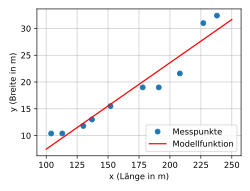
In the example graphic, data points and a compensation function are entered. A general function (the model function ) is selected that should fit the question and the data, here a logistical function . Their parameters are now determined in such a way that the sum of the squared deviations of the observations from the values of the function is minimized . In the graphic, the deviation at this point can be seen as a vertical distance between the observation and the curve.
In stochastics , the least squares method is mostly used as a regression analysis estimation method , where it is also referred to as least squares estimation or ordinary least squares estimation . Since the least squares estimation, the residual sum minimized, it is that estimation method which comprises of determination maximized. The method of least squares is used as system identification in connection with model tests e.g. B. for engineers a way out of the paradoxical situation of determining model parameters for unknown laws.
history

On New Year's Day 1801, the Italian astronomer Giuseppe Piazzi discovered the dwarf planet Ceres . He was able to follow the path for 40 days, then Ceres disappeared behind the sun. In the course of the year, many scientists tried unsuccessfully to calculate the orbit on the basis of Piazzi's observations - assuming a circular orbit, because at that time the orbit elements could only be mathematically determined from observed heavenly positions for such .
The 24-year-old Gauss managed to calculate the orbit with the help of a new indirect method of determining the orbit and his compensation calculations based on the method of the least squares (although not so designated) in such a way that Franz Xaver von Zach gave him on December 7, 1801 and - confirmed - was able to find it again on December 31, 1801. Heinrich Wilhelm Olbers confirmed this independently of Zach through observation on January 1 and 2, 1802.
The problem of finding the Ceres as such lay in the fact that neither the location, part of the path, nor the distance are known from the observations , only the directions of the observation. This leads to the search for an ellipse and not for a circle as suggested by Gauss's competitors. One of the focal points of the ellipse is known (the sun itself), and the arcs of the orbit of the Ceres between the directions of observation are traversed according to Kepler's second law , that is, the times behave like the surfaces swept by the guide beam. In addition, it is known for the computational solution that the observations themselves assume a conic section in space, the earth's orbit itself.
In principle, the problem leads to an equation of the eighth degree, the trivial solution of which is the earth's orbit itself. Through extensive constraints and (later) the method of least squares developed by Gauss, the 24-year-old managed to specify the location he had calculated for the orbit of the Ceres for November 25 to December 31, 1801. This enabled Zach to find Ceres on the last day of the forecast. The place was no less than 7 ° (i.e. 13.5 full moon widths ) east of where the other astronomers had suspected Ceres, which not only Zach but also Olbers duly appreciated.
His first calculations were still without the least squares method , only when a lot of new data became available after the rediscovery of Ceres, he used this for a more precise determination of the orbital elements, but without generally disclosing details of his method. Piazzi's reputation, which had suffered severely because of its path points that did not want to fit a circular path, was also restored.
A predecessor method of the method of least squares is the method of the smallest absolute deviation , which was developed in 1760 by Rugjer Josip Bošković . Gauss developed the principles of the least squares method as early as 1795 at the age of 18. It was based on an idea by Pierre-Simon Laplace to add up the deviations of the measured values from the expected value so that the sum of all these so-called errors resulted in zero. In contrast to this method, Gauss used the error squares instead of the errors and was thus able to dispense with the zero-sum requirement. Independently of Gauss, the Frenchman Adrien-Marie Legendre developed the same method, published it first in 1805, at the end of a little work on the calculation of comet orbits, and published a second treatise on it in 1810. Its presentation was extremely clear and simple. The name Méthode des moindres carrés (method of the smallest squares) also comes from Legendre .
In 1809, Gauss published in the second volume of his celestial mechanical work Theoria motus corporum coelestium in sectionibus conicis solem ambientium (theory of the movement of the celestial bodies, which revolve around the sun in conic sections), the method including the normal equations, as well as the Gaussian elimination method and the Gauss-Newton method which went far beyond Legendre. In it he referred to the least squares method as his discovery and claimed to have discovered and applied it as early as 1795 (i.e. before Legendre), which annoyed him for a long time. Legendre complained about it in a long letter to Gauss, which the latter left unanswered. Gauss only occasionally referred to an entry in his mathematical diary of June 17, 1798 (there is the cryptic sentence in Latin: Calculus probabilitatis contra La Place defensus (calculus of probability defended against Laplace) and nothing else). Laplace judged the matter in such a way that Legendre made the first publication, but Gauss undoubtedly knew the method beforehand, used it himself and also informed other astronomers by letter. The least squares method quickly became the standard method for handling astronomical or geodetic data sets after its publication.
Gauss used the method intensively in his survey of the Kingdom of Hanover by triangulation . The two-part work was published in 1821 and 1823, and in 1826 a supplement to Theoria combinationis observationum erroribus minimis obnoxiae (theory of the combination of observations subject to the smallest error) , in which Gauss justified the success of the least squares method by stating that it was compared to other methods the adjustment calculation is optimal in a broad sense. The mathematical formulation of this statement is known as Gauss-Markow's theorem, named after Andrei Andrejewitsch Markow , who rediscovered and made popular this part of Gauß's work, which was initially neglected, in the 20th century (see also Gauß-Markow's theorem ) . The Theoria Combinationis also contains methods for efficiently solving linear systems of equations , such as the Gauß-Seidel method and the LR decomposition , which represent a significant advance on the mathematical knowledge of the time.
The French surveying officer André-Louis Cholesky developed the Cholesky decomposition during the First World War , which again represented a considerable gain in efficiency compared to Gauss' solution method. In the 1960s, Gene Golub developed the idea of solving the occurring linear systems of equations using QR decomposition .
The procedure
requirements
One looks at a dependent variable that is influenced by one or more variables. The elongation of a spring depends only on the force applied, but the profitability of a company depends on several factors such as sales , the various costs or equity . To simplify the notation, the representation is limited to one variable in the following . The relationship between and the variables is established via a model function , for example a parabola or an exponential function
- ,
which depends on as well as on functional parameters. This function comes either from the knowledge of the user or from a more or less time-consuming search for a model; various model functions may have to be applied and the results compared. A simple case based on existing knowledge is, for example, the spring, because here Hooke's law and thus a linear function with the spring constant as the only parameter is a model requirement. However, in more difficult cases, such as that of the company, the choice of function type must be preceded by a complex modeling process .
In order to obtain information about the parameters and thus the specific type of relationship, corresponding observation values are collected for the given values of the independent variables . The parameters are used to adapt the selected function type to these observed values . The goal is now to choose the parameters so that the model function approximates the data as best as possible.
Gauss and Legendre had the idea of making distribution assumptions about the measurement errors of these observation values. They should be zero on average, have a constant variance and be stochastically independent of any other measurement error . This means that there is no longer any systematic information in the measurement errors, i.e. that they fluctuate around zero purely by chance. In addition, the measurement errors should be normally distributed , which on the one hand has probabilistic advantages and on the other hand guarantees that outliers are as good as excluded.
In order to determine the parameters under these assumptions , it is generally necessary that there are significantly more data points than parameters, so it must apply.
Minimizing the sum of the squares of errors
The criterion for determining the approximation should be chosen so that large deviations of the model function from the data are weighted more heavily than small ones. If no solution is possible without any deviations, then the compromise with the lowest overall deviation is the best generally applicable criterion.
For this purpose, the sum of the squares of the errors, which is also called the sum of the squares of the errors (more precisely: the sum of the squares of the residuals ), is defined as the sum of the squared differences between the values of the model curve and the data .
In formula notation with the parameters and results
Those parameters should then be selected for which the sum of the squared adjustment errors is minimal:
How exactly this minimization problem is solved depends on the type of model function.
If the error sum of squares is predicted for an external data set, one speaks of the PRESS statistics ( English predictive residual sum of squares ).
Linear model function
Linear model functions are linear combinations of any, generally non-linear basis functions. For such model functions, the minimization problem can also be solved analytically using an extreme value approach without iterative approximation steps. First some simple special cases and examples are shown.
Special case of a simple linear best-fit line
Derivation and procedure
The first order polynomial is a simple model function with two linear parameters
The coefficients and the best-fitting straight line are sought for the given measured values . The deviations between the straight line you are looking for and the respective measured values
are called fitting errors or residuals . We are now looking for the coefficients and with the smallest sum of the error squares
- .
The great advantage of the approach with this square of the errors becomes visible if this minimization is carried out mathematically: The sum function is understood as a function of the two variables and (the incoming measured values are numerical constants), then the derivative (more precisely: partial derivatives ) of the Function based on these variables (i.e. and ) and finally searched for the zero from this derivation . The result is the linear system of equations
with the solution
- and ,
where represents the sum of the deviation products between and , and represents the sum of the squared deviations of . It is the arithmetic mean of the values, accordingly. The solution for can also be found in non- centered form with the help of the displacement theorem
can be specified. These results can also be derived with functions of a real variable, i.e. without partial derivatives.
Example with a best-fit straight line
In this example, a best-fit straight line of the shape is calculated to show the relationship between two features of a data set. The data set consists of the length and width of ten warships (see warship data ). An attempt should be made to relate the latitude to the longitude. The data is presented in the first three columns of the following table. The other columns relate to intermediate results for calculating the best-fit straight line. The variable should designate the length of the warship and its width. What is sought is the straight line for which, if the known values are used, the function values are as close as possible to the known values .
| Warship | Length (m) | Width (m) | ||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 208 | 21.6 | 40.2 | 3.19 | 128.24 | 1616.04 | 24.88 | 3.28 |
| 2 | 152 | 15.5 | −15.8 | −2.91 | 45.98 | 249.64 | 15.86 | 0.36 |
| 3 | 113 | 10.4 | −54.8 | −8.01 | 438.95 | 3003.04 | 9.57 | −0.83 |
| 4th | 227 | 31.0 | 59.2 | 12.59 | 745.33 | 3504.64 | 27.95 | −3.05 |
| 5 | 137 | 13.0 | −30.8 | −5.41 | 166.63 | 948.64 | 13.44 | 0.44 |
| 6th | 238 | 32.4 | 70.2 | 13.99 | 982.10 | 4928.04 | 29.72 | −2.68 |
| 7th | 178 | 19.0 | 10.2 | 0.59 | 6.02 | 104.04 | 20.05 | 1.05 |
| 8th | 104 | 10.4 | −63.8 | −8.01 | 511.04 | 4070.44 | 8.12 | −2.28 |
| 9 | 191 | 19.0 | 23.2 | 0.59 | 13.69 | 538.24 | 22.14 | 3.14 |
| 10 | 130 | 11.8 | −37.8 | −6.61 | 249.86 | 1428.84 | 12.31 | 0.51 |
| Sum Σ | 1678 | 184.1 | 3287.82 | 20391.60 |
The best-fit line is determined by the coefficients and , which are calculated using as specified above
The constants and are respectively the average values of - and metrics, so
As a first intermediate step, the deviation from the mean value can now be calculated for each warship: and - these values are entered in the fourth and fifth columns of the table above. This simplifies the formula for
As a second intermediate step, the products and can be calculated for each warship. These values are entered in the sixth and seventh columns of the table and can now easily be added up. This can be calculated as
The value of can already be interpreted: Assuming that the data are linearly related and can be described by our calculated best-fit line, the width of a warship increases by approx. 0.16 meters for every whole meter that it is longer is.
The intercept is then
The equation of the best-fit line is thus
To illustrate this, the data can be plotted as a scatter diagram and the best-fit line inserted. The graph suggests that there is indeed a linear relationship between the length and width of a warship for our sample data. The adjustment of the points is quite good. The deviation of the values predicted by the straight line from the measured values can also be viewed as a measure . The corresponding values are entered in the eighth and ninth columns of the table. The average deviation is 2.1 m. The coefficient of determination , as a standardized coefficient, also gives a value of approx. 92.2% (100% would correspond to an average deviation of 0 m); for the calculation see the example for the coefficient of determination .
However, the negative intercept means that in our linear model a warship with a length of 0 meters has a negative width - or warships only begin to exist from a certain minimum length. Compared to reality, this is of course wrong, which can be taken into account when assessing a statistical analysis. It is probable that the model is only valid for the area for which the measured values are actually available (in this case for warship lengths between 100 m and 240 m) and that outside the area a linear function is no longer suitable to represent the data.
Simple polynomial best fit curves
Best-fit polynomials are more general than a linear best-fit line
- ,
which will now be illustrated using an example (such equalization polynomial approaches can - in addition to the iterative solution - be solved analytically using an extreme value approach).
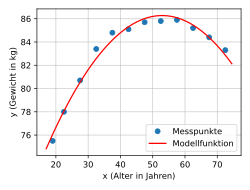
The results of the microcensus survey by the Federal Statistical Office are the average weights of men by age group (source: Federal Statistical Office, Wiesbaden 2009). For the analysis, the age groups were replaced by the middle classes. The dependence of the variable weight ( ) on the variable age ( ) is to be analyzed.
The scatter diagram suggests an approximately parabolic relationship between and , which can often be approximated well using a polynomial. It becomes a polynomial approach to the form
tries. The result is the 4th degree polynomial
- .
The measuring points deviate on average ( standard deviation ) 0.19 kg from the model function. If you reduce the degree of the polynomial to 3, you get the solution
with a mean deviation of 0.22 kg and for polynomial degree 2 the solution
with a mean deviation of 0.42 kg. As can be seen, if the higher terms are omitted, the coefficients of the lower terms change. The method tries to get the most out of every situation. Correspondingly, the missing higher terms are compensated as well as possible with the help of the lower terms until the mathematical optimum is reached. The second degree polynomial (parabola) describes the course of the measuring points very well (see figure).
Special case of a linear adjustment function with several variables
If the model function is a multi-dimensional polynomial of the first order, i.e. if it has several independent model variables instead of just one variable , a linear function of the form is obtained
- ,
those on the residuals
leads and about the minimization approach
can be solved.
The general linear case
In the following, the general case of any linear model functions with any dimension will be shown. For a given measured value function
with independent variables is an optimally adapted linear model function
sought whose quadratic deviation should be minimal. are the function coordinates, the linear incoming parameters to be determined and any linearly independent functions selected for adaptation to the problem.
At given measuring points
one obtains the adjustment errors
or in matrix notation
wherein the vector which summarizes which matrix the basis function values , the parameter vector , the parameters and the vector observations where .
The minimization problem using the Euclidean norm by
can be formulated in the regular case (i.e. has full column rank , so is regular and thus invertible) with the formula
can be solved clearly analytically, as will be explained in the next section. In the singular case, if is not of full rank, the system of normal equations cannot be solved uniquely, i.e. H. the parameter cannot be identified (see Gauss-Markow theorem # Singular case, estimable functions ).
Solution of the minimization problem
Derivation and procedure
The minimization problem results, as shown in the general linear case, as
This problem can always be solved. If the matrix has full rank , the solution is even unique. To determine the extremal point, zeroing the partial derivatives with respect to the ,
a linear system of normal equations (also Gaussian normal equations or normal equations )
which provides the solution of the minimization problem and generally has to be solved numerically. Has full rank and is , then the matrix is positive definite, so that the extremum found is indeed a minimum. In this way, solving the minimization problem of the linear model functions can be reduced to solving a system of equations. In the simple case of a best-fit straight line, its solution can, as shown, even be given directly as a simple formula.
Alternatively, the normal equations can be shown in the representation
write out, whereby the standard scalar product symbolizes and can also be understood as the integral of the overlap of the basic functions. The basic functions are to be read as vectors with the discrete support points at the location of the observations .
Furthermore, the minimization problem can be analyzed well with a singular value decomposition . This also motivated the expression of the pseudo inverse , a generalization of the normal inverse of a matrix . This then provides a perspective on non-square linear systems of equations that allow a not stochastically, but algebraically motivated solution concept.
Numerical treatment of the solution
There are two ways of solving the problem numerically. On the one hand, the normal equations
which are uniquely solvable if the matrix has full rank. Furthermore, the product sum matrix has the property of being positive definite , so its eigenvalues are all positive. Together with the symmetry of , this can be used for the solution when using numerical methods: for example with the Cholesky decomposition or the CG method . Since both methods are strongly influenced by the condition of the matrix, this is sometimes not a recommended approach: If the condition is already bad, then the quadratic is badly conditioned. As a result, rounding errors can be amplified to such an extent that they make the result unusable. However, regularization methods can improve the condition.
One method is the so-called ridge regression , which goes back to Hoerl and Kennard (1970). The English word ridge means something like ridge, reef, back. Instead of the poorly conditioned matrix, the better conditioned matrix is used here. Here is the -dimensional identity matrix. The art lies in the appropriate choice of . Too small increases the stamina only a little, too large leads to a distorted adaptation.
On the other hand, the original minimization problem provides a more stable alternative, since with a small value of the minimum it has a condition in the order of magnitude of the condition of , with large values of the square the condition of . A QR decomposition is used to compute the solution , which is generated with household transformations or Givens rotations . The basic idea is that orthogonal transformations do not change the Euclidean norm of a vector. So is
for every orthogonal matrix . To solve the problem, a QR decomposition of can be calculated, whereby the right-hand side is also transformed directly. This leads to a form
with where is a right upper triangular matrix . The solution to the problem is thus obtained by solving the system of equations
The norm of the minimum then results from the remaining components of the transformed right-hand side, since the associated equations can never be fulfilled due to the zero lines in .
In statistical regression analysis , given several variables, one speaks of multiple linear regression . The most common approach, a multiple linear model to estimate than the ordinary least squares estimation or ordinary least squares ( english ordinary least squares , shortly OLS ) known. Unlike the ordinary least squares method is generalized least squares method , short VMKQ ( English generalized least squares , shortly GLS ) in a generalized linear regression model used. In this model, the error terms deviate from the distribution assumption such as uncorrelatedness and / or homoscedasticity . In contrast, with multivariate regression there are many values for each observation , so that instead of a vector a matrix is present (see general linear model ). The linear regression models have been intensively researched in statistics in terms of probability theory. In econometrics in particular , for example, complex recursively defined linear structural equations are analyzed in order to model economic systems.
Constraint issues
Often additional information about the parameters is known, which is formulated by secondary conditions, which are then available in the form of equations or inequalities. For example, equations appear when certain data points are to be interpolated. Inequalities appear more frequently, usually in the form of intervals for individual parameters. The spring constant was mentioned in the introductory example; it is always greater than zero and can always be estimated upwards for the specific case under consideration.
In the case of an equation, these can be used for a reasonably posed problem in order to transform the original minimization problem into one of a lower dimension, the solution of which automatically fulfills the secondary conditions.
The inequality case is more difficult. The problem arises here with linear inequalities
- with ,
where the inequalities are meant component-wise. This problem can be solved unambiguously as a convex and quadratic optimization problem and can be approached, for example, with methods for solving such.
Quadratic inequalities arise, for example, when using a Tychonow regularization to solve integral equations . Solvability is not always given here. The numerical solution can, for example, be done with special QR decompositions .
Nonlinear model functions
Basic idea and procedure
With the advent of powerful computers, non-linear regression in particular is gaining in importance. The parameters are included in the function in a non-linear manner. Nonlinear modeling, in principle, allows data to be fitted to any equation of shape . Since these equations define curves , the terms nonlinear regression and "curve fitting" are mostly used synonymously.
Some nonlinear problems can be transformed into linear ones through suitable substitution and then solved as above. A multiplicative model of the form
can be converted into an additive system by taking the logarithm , for example . This approach is used, among other things, in growth theory .
In general, a problem of shape arises with nonlinear model functions
with a non-linear function . Partial differentiation then results in a system of normal equations that can no longer be solved analytically. A numerical solution can be done iteratively with the Gauss-Newton method . However, this has the disadvantage that the convergence of the method is not assured.
Current programs often work with one variant, the Levenberg-Marquardt algorithm . With this method, convergence is not guaranteed either, but regularization guarantees the monotony of the approximation sequence. In addition, the method is more tolerant than the original method if there is a greater deviation in the estimated values. Both methods are related to the Newton method and usually converge quadratically , so the number of correct decimal places doubles in each step.
If the differentiation is too time-consuming due to the complexity of the objective function, a number of other methods are available as alternative solutions that do not require any derivations, see methods of local non-linear optimization .
Example from enzyme kinetics of a non-linearizable model function
An example of regression models that are fully non-linear is enzyme kinetics . The requirement here is that "only" (reaction speed) and not (substrate concentration) is subject to an error and can thus be used as a variable. The Lineweaver-Burk relationship is an algebraically correct transformation of the Michaelis-Menten equation , but its application only provides correct results if the measured values are free of errors. This arises from the fact that reality only arises with an expanded Michaelis-Menten relationship
can be described with as an error parameter. This equation can no longer be linearized, so the solution must be determined iteratively here.
Misconduct if the requirements are not met
The least squares method allows the most probable of all model parameters to be calculated under certain conditions. To do this, a correct model must have been selected, a sufficient number of measured values must be available and the deviations of the measured values from the model system must form a normal distribution . In practice, however, the method can also be used for various purposes if these requirements are not met. However, it should be noted that the least squares method can give completely undesirable results under certain adverse conditions. For example, there should be no outliers in the measured values, as these distort the estimation result . In addition, multicollinearity between the parameters to be estimated is unfavorable because it causes numerical problems. Incidentally, regressors that are far from the others can also have a strong influence on the results of the adjustment calculation. One speaks here of values with great leverage ( English High Leverage Value ).
Multicollinearity
The phenomenon of multicollinearity arises when the measurements of two given variables and very high correlation are so are almost linearly dependent. In the linear case this means that the determinant of the normal equation matrix is very small and, conversely, the norm of the inverse is very large; the condition of is severely impaired. The normal equations are then difficult to solve numerically. The solution values can become implausibly large, and even small changes in the observations cause large changes in the estimates.
Runaway
Data values that "do not fit into a series of measurements" are defined as outliers . These values strongly influence the calculation of the parameters and falsify the result. To avoid this, the data must be examined for incorrect observations. The discovered outliers can be eliminated from the measurement series, for example, or alternative outlier-resistant calculation methods such as weighted regression or the three-group method can be used.
In the first case, after the first calculation of the estimated values, statistical tests are used to check whether there are outliers in individual measured values. These measured values are then rejected and the estimated values are calculated again. This method is suitable when there are only a few outliers.
In weighted regression, the dependent variables are weighted depending on their residuals . Outliers, d. H. Observations with large residuals are given a low weight, which can be graded depending on the size of the residual. In the algorithm according to Mosteller and Tukey (1977), which is referred to as “biweighting”, unproblematic values are weighted with 1 and outliers with 0, which means that the outlier is suppressed. With weighted regression, several iteration steps are usually required until the set of identified outliers no longer changes.
Generalized Least Squares Models
If the strong requirements in the procedure for the error terms are softened, so-called generalized least-squares approaches are obtained . Important special cases then have their own names, such as the weighted least squares ( english weighted least squares , shortly WLS ) in which the errors are indeed further assumed to be uncorrelated, but not more of the same variance. This leads to a problem of form
where D is a diagonal matrix . If the variances vary greatly, the corresponding normal equations have a very large condition , which is why the problem should be solved directly.
If one further assumes that the errors in the measurement data should also be taken into account in the model function, the “total least squares” result in the form
where the error is in the model and the error is in the data.
Finally, there is also the option of not using a normal distribution as a basis. This corresponds, for example, to the minimization not in the Euclidean norm, but in the sum norm . Such models are subjects of regression analysis .
literature
- Åke Björck: Numerical Methods for Least Squares Problems. SIAM, Philadelphia 1996, ISBN 0-89871-360-9 .
- Walter Großmann: Fundamentals of the equalization calculation. 3rd ext. Edition. Springer Verlag, Berlin / Heidelberg / New York 1969, ISBN 3-540-04495-7 .
- Richard J. Hanson, Charles L. Lawson: Solving least squares problems. SIAM, Philadelphia 1995, ISBN 0-89871-356-0 .
- Frederick Mosteller , John W. Tukey : Data Analysis and Regression - a second course in statistics. Addison-Wesley, Reading MA 1977, ISBN 0-201-04854-X .
- Gerhard Sacrifice: Numerical Mathematics for Beginners. An introduction for mathematicians, engineers and computer scientists. 4th edition. Vieweg, Braunschweig 2002, ISBN 3-528-37265-6 .
- Peter Schönfeld: Methods of Econometrics. 2 volumes. Vahlen, Berlin / Frankfurt 1969–1971.
- Eberhard Zeidler (Hrsg.): Pocket book of mathematics. Justified v. IN Bronstein, KA Semendjajew. Teubner, Stuttgart / Leipzig / Wiesbaden 2003, ISBN 3-8171-2005-2 .
- T. Strutz: Data Fitting and Uncertainty (A practical introduction to weighted least squares and beyond). 2nd edition. Springer Vieweg, 2016, ISBN 978-3-658-11455-8 .
Web links
Individual evidence
- ^ Moritz Cantor : Gauß: Karl Friedrich G. In: General German Biography (ADB). Volume 8, Duncker & Humblot, Leipzig 1878, pp. 430–445., Here p. 436.
- ↑ Paul Karlson: Magic of Numbers. Ullstein-Verlag, Berlin-West. Ninth, revised and expanded edition, 1967, p. 390 f.
- ^ A. Abdulle, Gerhard Wanner : 200 years of least square methods . In: Elements of Mathematics , Volume 57, 2002, pp. 45-60, doi: 10.1007 / PL00000559 .
- ↑ Cf. Moritz Cantor : Gauß: Karl Friedrich G. In: Allgemeine Deutsche Biographie (ADB). Volume 8, Duncker & Humblot, Leipzig 1878, pp. 430-445., P. 436.
- ^ Adrien-Marie Legendre: Nouvelles méthodes pour la détermination des orbites des comètes. Paris 1805, pp. 72–80 (Appendix): Sur la Méthode des moindres quarrés.
- ^ Carl Friedrich Gauß: Theoria Motus Corporum Coelestium in sectionibus conicis solem ambientium . Göttingen 1809; Carl Haase (transl.): Theory of the movement of the heavenly bodies, which revolve around the sun in conic sections. Hanover 1865.
- ^ Matrices and determinants .
- ↑ Printed in Gauß, Werke, Volume X / 1, p. 380.
- ^ Abdulle, Wanner: Elements of mathematics . Volume 57, 2002, p. 51. With facsimile copy of the diary entry.
- ^ Laplace, quoted from Herman Goldstine: A history of numerical analysis . Springer, 1977, p. 209.
- ^ Carl Friedrich Gauß: Theoria combinationis observationum erroribus minimis obnoxiae. 2 parts. Göttingen 1821–1823 (Commentationes Societatis Regiae Scientiarum Gottingensis recentiores, classis mathematicae, Volume 5.); Supplementum Theoria combinationis observationum erroribus minimis obnoxiae. Göttingen 1826/28 (Commentationes Societatis Regiae Scientiarum Gottingensis recentiores, classis mathematicae, Volume 6.). Anton Börsch Paul Simon (Ed.): Treatises on the least squares method by Carl Friedrich Gauss. In German language. Berlin 1887, Textarchiv - Internet Archive .
- ↑ Pete Stewart: Maybe We Should Call It “Lagrangian Elimination” . NA Digest Sunday, June 21, 1991, June 30, 1991 Volume 91, Issue 26.
- ↑ H. Wirths: Relational Mathematics in Regression and Correlation . In: Stochastik in der Schule , 1991, Issue 1, pp. 34–53
- ↑ Hans R. Schwarz, Norbert Köckler: Numerical Mathematics. 7. revised Edition. Teubner, 2009, doi: 10.1007 / 978-3-8348-9282-9 , ISBN 978-3-8348-9282-9 , p. 141, chapter 3.6 (Gaussian approximation), sentence 3.23.
- ↑ AE Hoerl and RW Kennard: Ridge regression: Biased estimation for nonorthogonal problems , Techno Metrics 12 (1970), 55-82.
- ^ Sabine Van Huffel, Joos Vandewalle: The Total Least Squares Problem: Computational Aspects and Analysis. SIAM Publications, Philadelphia PA 1991, ISBN 0-89871-275-0 .
- ↑ Martin Plesinger: The Total Least Squares Problem and Reduction of Data in AX ≈ B. Dissertation. ( Memento of July 24, 2012 in the Internet Archive ; PDF; 1.6 MB) TU Liberec and ICS Prague, 2008.


















































































































![v = V _ {\ mathrm {max}} \ cdot [S] / (K_ {m} + [S])](https://wikimedia.org/api/rest_v1/media/math/render/svg/27b2ab027f6b145dee50e5c62c28ad91d2f75e7c)
![\ nu _ {i} = {\ frac {V _ {\ max} \ left [S_ {i} \ right]} {K_ {m} + \ left [S_ {i} \ right]}} (1 + e_ { i}) \ {\ boldsymbol {\ nu}} _ {i}](https://wikimedia.org/api/rest_v1/media/math/render/svg/97c97305e52d0907f8094ccf03835e53137f9f9b)





