Sum norm

Sum norm in two dimensions

The sum norm , amount sum norm or 1-norm is a vector norm in mathematics . It is defined as the sum of the amounts of the vector components and is a special p -norm for the choice of . The unit sphere of the real sum norm is a cross polytope with minimal volume over all p norms. Hence the sum norm for a given vector gives the largest value of all p norms. The metric derived from the sum norm is the Manhattan metric . ${\displaystyle p=1}$

definition

If an n -dimensional vector with real or complex entries for , then the sum norm of the vector is defined as ${\displaystyle x=(x_{1},x_{2},\ldots ,x_{n})}$ ${\displaystyle x_{i}}$ ${\displaystyle i=1,\ldots ,n}$ ${\displaystyle \|\cdot \|_{1}}$

${\displaystyle \|x\|_{1}:=\sum _{i=1}^{n}|x_{i}|}$.

The sum norm thus corresponds to the sum of the amounts of the components of the vector and is therefore also called a somewhat more precise amount sum norm. It is a special p -norm for the choice of and is therefore also called 1-norm. ${\displaystyle p=1}$

Examples

Real vector

The sum norm of the real vector is given as ${\displaystyle x=(3,-2,6)\in \mathbb {R} ^{3}}$

${\displaystyle \|x\|_{1}=|3|+|{-2}|+|6|=11}$.

Complex vector

The sum norm of the complex vector is given as ${\displaystyle x=(3-4i,{-2i})\in \mathbb {C} ^{2}}$

${\displaystyle \|x\|_{1}=|3-4i|+|{-2i}|=5+2=7}$.

properties

Standard properties

Like all p- norms, the sum norm fulfills the three norm axioms , which are particularly easy to show here. The definiteness follows from the uniqueness of the zero of the absolute value function through

${\displaystyle \|x\|_{1}=0\;\Leftrightarrow \;\sum _{i=1}^{n}|x_{i}|=0\;\Rightarrow \;x=(0,\ldots ,0)=0}$,

the absolute homogeneity follows from the homogeneity of the amount standard on

${\displaystyle \|\alpha \cdot x\|_{1}=\sum _{i=1}^{n}|\alpha \cdot x_{i}|=\sum _{i=1}^{n}|\alpha |\cdot |x_{i}|=|\alpha |\cdot \sum _{i=1}^{n}|x_{i}|=|\alpha |\cdot \|x\|_{1}}$

and the subadditivity follows directly from the triangle inequality for real or complex numbers

${\displaystyle \|x+y\|_{1}=\sum _{i=1}^{n}|x_{i}+y_{i}|\leq \sum _{i=1}^{n}|x_{i}|+|y_{i}|=\sum _{i=1}^{n}|x_{i}|+\sum _{i=1}^{n}|y_{i}|=\|x\|_{1}+\|y\|_{1}}$.

Unity sphere

The unit sphere of the sum norm is an octahedron in three dimensions

The unit sphere of the real sum norm, i.e. the set

${\displaystyle \{x\in \mathbb {R} ^{n}:\|x\|_{1}=1\}}$

has the shape of a square in two dimensions, the shape of an octahedron in three dimensions and the shape of a cross polytop in general dimensions . The volume of the unit sphere of the sum norm is minimal across all p norms; it amounts to . ${\displaystyle {\tfrac {2^{n}}{n!}}}$

Comparison with the other p norms

The sum norm is the largest of all p -norms, that is, for a given vector, and holds ${\displaystyle x}$ ${\displaystyle 1<p\leq \infty }$

${\displaystyle \|x\|_{1}\geq \|x\|_{p}}$,

where equality applies if and only if the vector is the zero vector or a multiple of a unit vector . Conversely, due to the equivalence of norms in finite-dimensional vector spaces , the sum norm can pass upwards against every p norm

${\displaystyle \|x\|_{1}\leq n^{1-{\frac {1}{p}}}\cdot \|x\|_{p}}$

can be estimated, where equality holds for a constant vector. The equivalence constant with respect to the maximum norm is the same , which is the maximum between all p norms. ${\displaystyle (p=\infty )}$ ${\displaystyle n}$

Applications

Derived terms

The Manhattan metric is the distance between two points if you are only allowed to move on one grid. This distance is independent of which path you take (here 12).

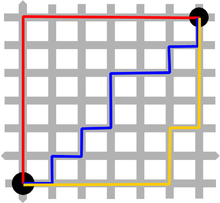
In contrast to the Euclidean norm (2-norm), the sum norm is not induced by a scalar product . The derived from the sum norm metric is the Manhattan metric or taxi metric

${\displaystyle d(x,y)=\sum _{i=1}^{n}|x_{i}-y_{i}|}$.

In real two-dimensional space, it measures the distance between two points like the route on a grid-shaped city map, on which one can only move in vertical and horizontal sections. The matrix norm induced by the sum norm is the column sum norm .

Amount of multi-indices

The sum norm is often used as the amount of a multi-index with non-negative entries. For example, a partial derivative of a function of several variables than ${\displaystyle \alpha =(\alpha _{1},\dotsc ,\alpha _{n})}$ ${\displaystyle f(x_{1},\dotsc ,x_{n})}$

${\displaystyle f^{(\alpha )}={\frac {\partial ^{|\alpha |}f}{\partial x_{1}^{\alpha _{1}}\dotso \partial x_{n}^{\alpha _{n}}}}={\frac {\partial ^{\alpha _{1}+\dotsb +\alpha _{n}}f}{\partial x_{1}^{\alpha _{1}}\dotso \partial x_{n}^{\alpha _{n}}}}}$

are written, in which case the order is the derivative. ${\displaystyle |\alpha |=\|\alpha \|_{1}}$

Generalizations

The sum norm can also be generalized to infinite-dimensional vector spaces over the real or complex numbers and then has its own name.

ℓ ¹ standard

The ℓ ¹ norm is the generalization of sum norm on the sequence space of the amount as summable consequences . Here only the finite sum is replaced by an infinite one and the ℓ ¹ norm is then given as ${\displaystyle \ell ^{1}}$ ${\displaystyle (a_{n})_{n}\in {\mathbb {K} }^{\mathbb {N} }}$

${\displaystyle \|(a_{n})\|_{\ell ^{1}}=\sum _{n=1}^{\infty }|a_{n}|}$.

L ¹ standard

Furthermore, the summation norm can be generalized to the function space of the functions that can be integrated on a quantity by amount , which happens in two steps. First, the -norm is an absolute Lebesgue integrable function as ${\displaystyle L^{1}(\Omega )}$ ${\displaystyle \Omega }$ ${\displaystyle {\mathcal {L}}^{1}}$ ${\displaystyle f\colon \Omega \rightarrow {\mathbb {K} }}$

${\displaystyle \|f\|_{{\mathcal {L}}^{1}(\Omega )}=\int _{\Omega }|f(x)|\,dx}$,

defined, whereby in comparison to the ℓ ¹ norm only the sum was replaced by an integral. This is initially only a semi-norm , since not only the null function but also all functions that differ from the null function only in terms of a set with Lebesgue measure zero are integrated to zero. Therefore, considering the amount of equivalence classes of functions that are almost the same everywhere, and gets on that L ¹ -space the L ¹ norm by ${\displaystyle [f]\in L^{1}(\Omega )}$

${\displaystyle \|\,[f]\,\|_{L^{1}(\Omega )}=\|f\|_{{\mathcal {L}}^{1}(\Omega )}}$.

literature

• Hans Wilhelm Alt: Linear Functional Analysis: An Application-Oriented Introduction . 5th edition. Springer-Verlag, 2008, ISBN 3-540-34186-2 .
• Rolf Walter: Introduction to Analysis 2 . de Gruyter, 2007, ISBN 978-3-11-019540-8 .

Web links

• Eric W. Weisstein : L ^ 1 norm . In: MathWorld (English).

Individual evidence

1. ^ Rolf Walter: Introduction to Analysis 2 . S. 37 .