Dot product norm
A Skalarproduktnorm , inner product standard or Hilbert norm is in the mathematics one of a scalar product induced (derived) standard . In a finite-dimensional real or complex vector space with the standard scalar product, the scalar product norm corresponds precisely to the Euclidean norm . In general, every Prähilbert space has an assigned scalar product norm and is a normalized space with this norm . A norm is induced by a scalar product if and only if it satisfies the parallelogram equation. Every dot product norm still satisfies the Cauchy-Schwarz inequality and is invariant under unitary transformations .
definition
If there is a vector space over the field of real or complex numbers and an inner product on , then is an inner product space . The induced by this inner product standard is for a vector then defined as
- ,
thus the root of the scalar product of the vector with itself. This definition is well defined, since the scalar product of a vector with itself is real and nonnegative.
This norm is also called scalar product norm, inner product norm or Hilbert norm and is sometimes referred to as (general) Euclidean norm in real scalar product spaces . With the scalar product norm, the vector space is a normalized space . Furthermore, the metric induced by the standard is a metric space and the standard topology is a topological space .
Examples
Important examples of scalar product norms are:
- the Euclidean norm on the Euclidean space of finite-dimensional vectors,
- the ℓ 2 norm on the space ℓ 2 of the quadratically summable sequences,
- the L 2 norm on the space L 2 of the square Lebesgue integrable functions,
- the Sobolev norm on the Sobolev space H s of the functions whose mixed weak derivatives are Lebesgue integrable up to the degree quadratically,
- the Frobenius norm on the space of the matrices ,
- the Hilbert-Schmidt norm in the space of the Hilbert-Schmidt operators .
properties
Norm axioms

Every scalar product norm fulfills the three norm axioms definiteness , absolute homogeneity and subadditivity . The definiteness follows from the uniqueness of the root of the root function above
- ,
absolute homogeneity follows for and from
and the subadditivity (or triangle inequality ) follows for from the Cauchy-Schwarz inequality (see the following section)
where indicates the real part of the complex number and in the last two cases the (positive) root has to be drawn on both sides.
Parallelogram equation
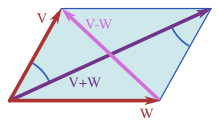
The parallelogram equation also applies to a scalar product norm
for all vectors . Conversely, according to Jordan-von Neumann's theorem, if a norm fulfills the parallelogram equation , it is induced by a scalar product. This result is obtained by a polarization formula , for real vector spaces for example by
- .
Unitary invariance
A dot product norm is still invariant under unitary transformations . If there is a unitary operator (in the finite-dimensional case a unitary or orthogonal matrix ) from into a further scalar product space with an associated norm, then applies
- ,
what immediately
follows, where the operator to be adjoint (in the finite-dimensional case the adjoint or transposed matrix ) is. A scalar product norm does not change its value under unitary transformations of the vector. In the real, finite-dimensional case, such transformations are, for example, rotations of the vector around the zero point .
Cauchy-Schwarz inequality
A scalar product norm satisfies the Cauchy-Schwarz inequality for all vectors
- ,
where equality applies if and only if and are linearly dependent . In the real case, the amount bars can also be omitted. The Cauchy-Schwarz inequality then immediately follows
- ,
therefore we can use the angle between two real vectors
define. The angle is thus in the interval , i.e. between and . There are a number of different definitions for angles between complex vectors.
Pythagorean theorem
In general, two vectors are said to be orthogonal if their is a scalar product . The Pythagorean theorem for scalar product spaces then applies to orthogonal vectors
- ,
which follows directly from the first part of the above derivation of the triangle inequality. The Pythagorean theorem can also be extended to a finite sum of pairwise orthogonal vectors and it then applies
- .
The corresponding extension to an infinite number of summands in a Hilbert space is Parseval's equation .
generalization
If one waives the positive definiteness of the scalar product, one obtains the following generalization. Every positive semidefinite Hermitian sesquilinear form (in the real case symmetrical bilinear form ) induces for by
a semi-norm . With this semi-standard there is then a semi- standardized space , which is generally not a metric space. By forming residual classes , however, an associated standard can be derived from a semi-standard and thus a standardized space and thus also a metric and a topological space are obtained.
example
The covariance is a bilinear form on the space of the random variables with finite second moments , and becomes a scalar product on the quotient space of the random variables, which only differ by one constant. The norm induced by this scalar product is then simply the standard deviation of a random variable.
literature
- Herbert Amann, Joachim Escher : Analysis I . Birkhäuser, Basel 2006, ISBN 3-7643-7755-0 .
- Albrecht Beutelspacher : Linear Algebra . 6th edition. Vieweg, 2003, ISBN 3-528-56508-X .
- Bronstein et al .: Paperback of Mathematics . 7th edition. Harri Deutsch, 2008, ISBN 978-3-8171-2007-9 .
- Harro Heuser : Functional Analysis: Theory and Application . Vieweg, 2006, ISBN 978-3-8351-0026-8 .
Individual evidence
- ↑ Kosmol: Optimization and Approximation . de Gruyter, 2010, p. 100 .
- ↑ Heuser: Functional Analysis: Theory and Application . 2006, p. 148 .
- ↑ Amann, Escher: Analysis I . 2006, p. 168 .
- ^ Bronstein et al .: Taschenbuch der Mathematik . 2008, p. 368 .
- ↑ Beutelspacher: Linear Algebra . 2003, p. 259 .
- ^ Klaus Scharnhorst: Angles in complex vector spaces . In: Acta Applicandae Math. Volume 69 , 2001, p. 95-103 .



































![[0, \ pi]](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e2a912eda6ef1afe46a81b518fe9da64a832751)








