angle
In geometry, an angle is a part of the plane that is delimited by two rays (half-straight lines) lying in the plane with a common starting point.
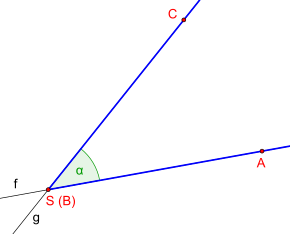
The common starting point of the two rays is called the vertex of the angle, angled vertex or vertex for short ; the rays are called the legs of the angle . An angle can be defined by three points , one of which forms the vertex of the angle and the other two lie on each leg of the angle.
The physical quantity that describes the relative position of the rays to each other is referred to as the angular width or angular distance (angular distance) , usually also in shortening as the angle , if a differentiation from the geometric object is not necessary, for example in physics . The size of the angle is specified with a square measure .
The angular width can also be defined as a measure of a plane rotation .
To distinguish it from the solid angle , the angle defined here is also referred to as a plane angle .
definition
In geometry, different approaches are possible for defining the angle as an object . Two types can be distinguished:
- The undirected angle , which is characterized by an unsigned angle width.
- The directed angle that has an orientation and is measured as a rotation angle or angular distance.
Representation as a pair of rays
The definition of two rays emanating from a point mentioned at the beginning is integrated into the applications such as the coordinate systems and their axes.
Representation as a half-line pair
The angle is a geometric structure consisting of two half-lines with the same origin.
- Are , two straight lines , which at one point cut, the point divides the line , in half-lines. A half-straight from and (the legs ) together with (the vertex ) form an angle.
Using the “original” straight line, this representation enables, for example, observations over the various pairs of angles.
Representation as part of the plane
- The angle (better: the angular field ) is a part of the plane of the drawing that is delimited by two half-rays or half-straight lines. These form the edge, and the rest of the angular field the inside.
This definition is used in school lessons and emphasizes the "physical" nature of the structure and serves - by defining an interior and exterior space - as an introduction to triangular geometry : The triangle can be defined as the intersection of two angles with a common leg.
Ad hoc, in these three approaches, the angle is an undirected angle; only an additional marking of one of the two half-rays or half-straight lines as the “first” enables a directed angle to be specified.
Representation as rotation
One can also say that an angle is created by a rotation of a ray or a half-line in a plane around its starting point.
Since there are two different ways of rotating the beam, the direction of rotation must also be specified:
- Left rotation : counter-clockwise, also called mathematically positive direction of rotation (angle is positive) - shown in green in the picture .
- Right rotation : clockwise, also called mathematically negative direction of rotation (angle is negative) - shown in purple in the picture .
In mathematics , it is common to rotate counterclockwise - i.e. in the mathematically positive direction of rotation . If the rotation is to be done the other way around, this should be stated explicitly.
In geodesy (surveying) the angle is counted clockwise, i.e. clockwise from 0 gon to 400 gon. Since there are by definition no negative angles in geodesy, the direction of rotation is positive. Analogous to the clock, here, too, counting is positive, clockwise, from 0 to 24 hours. All geodetic measuring instruments are turned to the right for direction or angle measurement.
Designation of angles
An angle is specified in accordance with DIN 1302 or ISO 80000-2 .
- Angles are usually written in small Greek letters , e.g. B. or , designated.
- An angle is an angle between two half-rays, straight lines, edges and the like. It is then counted from the starting direction .
- Alternatively, you can specify the three points that define the angle, with the vertex always in the middle, e.g. B. ABC angle, or out of date . This is the angle between and , wherein in the mathematically positive sense of rotation to be rotated.
- In the English- speaking world, only indicating the parting or is common.
The character »∠« ( HTML / , TeX , Unicode U + 2220) is available for the formula set , and »∡« (TeX , U + 2221 measured angle , no HTML entity) for the directional angle , both of which are in the Find Unicode Block Mathematical Operators . The lying angle symbol corresponds to the Anglo-American customs, in the European set of formulas a symbol is common that looks confusingly similar to the American "∢" U + 2222 for the solid angle . »∠« is also used for inclination and angularity ( positional tolerance , DIN EN ISO 1101). Especially for the right angle one uses »∟«, a dotted angle, in technology also a square, or .
∠∠ \angle\measuredangle
Angle measurements and units of measurement for angles
The main article angular dimensions provides detailed information , conversions can be found under the individual dimensions.
| Angle measure | Unit of measurement | 1 full angle = | Unit symbol |
|---|---|---|---|
| - | Full angle | 1 | |
| Radians | Radians | 2 π | wheel |
| Degree | Degree ( arc minute , arc second ) | 360 | ° (′ ″) |
| Geodetic angle measure | Gon (obsolete: grads) | 400 | gon (outdated: g ) |
| Measure of time | Hours minutes seconds | 24 | h m s |
| - | Nautical line | 32 | ¯ |
| - | Artillery line (Switzerland: Artilleriepromille) | 6400 | mil (A ‰) |
| - | Percent , per mille | non-linear | %, ‰ |
Further forms of specifying an angle:
- The tangent of the angular width of the pitch angle (also called pitch , corresponds to the dimension in percent)
- A pair with cosine and sine (corresponds to the Cartesian coordinates of the point on the unit circle )
Types of angles
- Zero angle
- acute angle
- smaller than full angle ( or );
- right angle
- equal to full angle: ;
- obtuse angle
- greater than full angle ( or ) and smaller than full angle ( or );
- straight angle
- equal to full angle: ;
- obtuse (raised) angle
- greater than full angle ( or ) and smaller than full angle ( or );
- full angle, full angle (full circle)
- .
There are four angles between two straight lines that intersect . Any two adjacent to each other add up . The peculiarity of the right angle is that these two angles are exactly the same. Two opposite angles are always the same. The peculiarity of the full angle is that two of the angles are zero .
Two straight lines or lines that intersect at right angles are called orthogonal to each other . In a drawing, the right angle is represented by a quarter circle with a point or a square .
The full angle is a legal unit in metrology in Germany, Austria and Switzerland , it does not have a unit symbol.
Special pairs of angles
Geometry has special terms for pairs of angles that have a special relationship to one another. The laws that apply to such angles help in the study of more complex geometric objects.
Complement angle or complementary angle
Two angles are called complement angles or complementary angles when they complement each other to form a right angle ( ).
Supplementary angle or supplementary angle
Two angles are called supplementary angle (also: supplementary angle ), supplement , supplementary angle or E-angle for short if they complement each other.
Secondary angle
If two straight lines intersect, a pair of neighboring angles is called a minor angle .
- Side angles complement each other .
So they are supplement angles.
Vertex angle or opposite angle
Intersect two straight lines, one refers to the pair of opposite angle than the apex angle or opposite angle .
- The vertex angles are always the same.
The term vertex angle comes from the fact that the two angles are mapped onto one another by point reflection at the vertex.
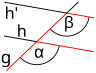
Step angle or F angle
If a straight line intersects two straight lines and , the angles that lie on the same side of and on corresponding sides of or are called step or F angles . In the event that the straight lines and are parallel, the following applies:
- Step angles at parallels are the same.
From the angular equality can be reversed closed on the parallelism of straight lines: If a pair of lines , by a further straight cut so that the cut angle on the same side of and on each respective sides of and are equal, so the lines are found and parallel.
Alternating angle or Z angle
If a straight line intersects two straight lines and , the angles that lie on different sides of and opposite sides of or are called alternating or Z angles . In the event that the straight lines and are parallel, the following applies:
- Alternating angles at parallels are the same.
From the angular equality can be reversed closed on the parallelism of straight lines: If a pair of lines , by a further straight cut so that the cut angles on different sides of and different sides of or are equal, so the lines are found and parallel.
Neighboring angle or E angle
If a straight line intersects two other parallel straight lines and , the angles that lie on the same side of but on different sides of and are called neighboring or E angles .
- Neighboring angles complement each other .
From integration of the angle to be reversed closed on the parallelism of straight lines: If a pair of lines , by a further straight cut so located that the angle of intersection, on the same side of , but in each case on different sides of and are, to 180 ° complement, the straight lines and are parallel.
The property that neighboring angles complement one another follows directly from the axiom of parallels in Euclidean geometry . The above-mentioned properties of step and alternating angles can be derived from the consideration of secondary and vertex angles of neighboring angles.
Angle with pairs of right-angled legs
Two angles, the legs of which are perpendicular to each other in pairs, are of the same size or complement each other . Compare the figures on the right.
Angular construction
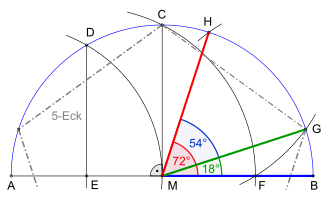
Some angles can be constructed with a compass and ruler alone . These include the 90-degree, 60-degree, 72-degree and 54-degree angle, as well as all angles that result from doubling, halving, adding or subtracting (see below) these angles.
The angles can be constructed in decimal degrees as an approximate construction using the third theorem of rays in combination with straight lines.
Construction of the 90 degree angle (right angle)
More precisely, one constructs the perpendicular to an already given route .
Construction for a given intersection on the straight line
- Draw a circle around with any radius. This circle cuts in two points.
- Draw a circle around each of these two points. The radii of the two circles must be chosen so that the circles intersect at two points.
- Connect the two intersections of these circles with a straight line. The straight line drawn in this way intersects at a right angle and precisely at the point .
Construction for a given point outside the straight line (falling the perpendicular)
- Draw a circle with a radius larger than the distance of the point from the straight line. This circle cuts in two points.
- The further procedure corresponds to the construction for a given intersection.
Construction (without specified intersection)
For any point of intersection, there is no need to define symmetrical points on the straight line
- Choose two points and on the straight line, and for these two points two circle radii large enough that the corresponding circles around and at two points - hereinafter referred to as and - intersect.
- Draw these two circles (they just have to be drawn so that the two intersection points can be seen).
- Draw the straight line going through the two intersections and . This straight line is perpendicular to .
Hints
You don't have to draw the circles completely. It is sufficient if the intersection points are recognizable. In principle, the greater the distance between the two intersection points, the more precise the construction. This is because the greater the distance, the smaller the effects of such errors, which arise because the newly drawn straight line or the intersection points already drawn do not exactly match the ideal intersection points. On the other hand, the more flatter the circles intersect, the less the exact detectability of the intersection points, which is the more the case, the further the circle radii are away from an ideal radius at which the circles intersect perpendicularly.
Halving the route, vertical center line
A given line is halved by choosing the endpoints and the line as the center points of two equal arcs and connecting their two common points of intersection and with each other. The intersection point thus created provides the center of the route that is sought .
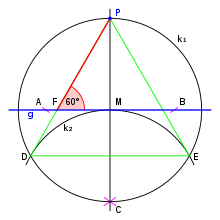
Construction of a 60 degree angle
Request a 60 degree angle to a straight line at a given vertex
- Draw a circle on the straight line around the given point (see below). The two points of intersection and .
- Draw a circle with the same radius z. B. around the point of intersection (alternatively around ) and mark the intersection of the two circles above the straight line as the point of intersection .
- Draw a straight line through the point and the intersection. Thus, the straight line at the vertex intersects the straight line at an angle of
Applying a 60 degree angle to a straight line through a point outside the straight line
- Drop the perpendicular from the given point onto the straight line (see above). You get the auxiliary points and and the counterpoint. The intersection is the base point
- Draw a circle ( ) around the base point through the given point.
- Draw an arc ( ) around the opposite point with the same radius. You will get the points and the straight line connecting them is the perpendicular of the line .
- Draw the equilateral triangle. The adjacent sides intersect the straight line in the desired way.
The figure on the right shows an alternative procedure which, in addition to the given point and the given straight line, only requires four circles with the same radius and the straight line for the solution. In the course of the construction, two points are always used to draw a circle. The distance between the two points is equal to the radius of the circle, so a so-called Euclidean or collapsing circle could also be used.
- Draw a circle with any radius , it will result in the intersection on the straight line
- Prefer having the same radius circle around the second point and the third circle around the just created point to intersect the circle in the distances from the points and to the line are equal.
- Finally, pull the fourth circle of the circle in cuts, and draw the line through the points and you cut the line at the apex and thus returns the angle with the desired angular width
Construct a 72, 54, or 18 degree angle
The somewhat more exotic construction of a 72 or 54 degree angle can be found in the regular pentagon .
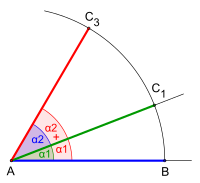
Addition and subtraction of angles
Every angle can be constructively, i.e. geometrically, added to and subtracted from another angle. In other words, you want to z. B. (see three pictures) to increase or decrease an angle by the size of another, first draw a circular arc of equal size for both angles around the vertices of the angles, which intersects or touches both legs of the respective angle.
- Add angles
First, the circular arc of the first angle over extended out so that it also, the second angle is sufficient space. Now take the angular width at the distance in the compass and use it to transfer it from the point of intersection to the extended arc. The result is the intersection. Finally, the new angle leg is drawn in.
The total angle thus generated by geometric addition has the angle width
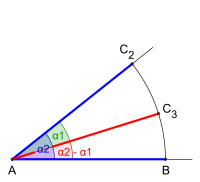
- Subtract the angle
In order to subtract the smaller angle from the larger angle (picture: angle width and ), take the angle width at the distance in the compass and use it to transfer it from the point of intersection to the arc. The point of intersection is then the new angle leg is drawn in.
The difference angle thus generated by geometric subtraction has the angle width
Angular divisions
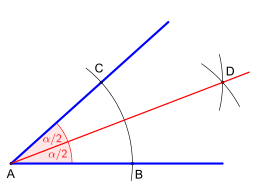
Bisecting the angle
An angle always consists of two legs that meet at the vertex. If you now draw two circles of the same size on each leg through the apex, the line between the points of intersection of the circle forms the bisector . Every point on the bisector is equidistant from the legs.
- construction
The first drawn circular arc about the vertex with an arbitrary radius, intersecting the side of the angle in and will now be either of the same (see Figure) or with a different circular aperture to the intersection points and respectively beaten an equal arc. Finally, from the apex , a half-line is drawn through the last intersection point and thus the bisector is obtained.
Tripartite
The general three-way division of the angle is not possible with Euclidean tools. However, there are (hand) drawing devices (e.g. tomahawk ) for this task. What is also possible, however, are approximation constructions with low angle errors.
Any division
The arbitrary division requires an aid with which an angle can be mapped proportionally on a line and vice versa, for example a template with an edge shaped as an Archimedean spiral or a quadratic rix of Hippias . This enables an angle division to be converted into a route division. There are applications of this in the construction of certain regular polygons that cannot be constructed with compasses and rulers alone, such as B. the elf .
Conclusion (general angle constructions)
If you construct the above angles (90 °, 60 °, 72 ° or 54 ° or their sums or differences ), further angles (45 °, 30 °, 36 ° and 27 ° or the associated sums) can be made from these by bisecting the angle or differences), which and their descendants can be halved again. The angle 3 ° is obtained z. B. by the following procedure: 72 ° / 2 → 36 ° / 2 → 18 ° - 15 ° = 3 °. In general, all angles can be constructed whose sine (and thus also their cosine ) can be represented by a mathematical expression that only consists of whole numbers, basic arithmetic operations and square roots. This applies e.g. B. for integer angles (degrees) that are a multiple of 3 °:
The halving of the angle can be achieved by substituting the half-angle formulas
- and
be expressed. The application of one angle to another can be done by substituting the addition theorems
- and
be expressed.
In addition, the cosine of the central angle of the 17-sided has the value:
- ,
from which its constructibility results.
Angle measurement
When measuring angles, technical equipment is used to determine the angle at which two straight lines or two other directions are to one another.
Web links
- Approximate construction of an angle in decimal degrees using the third theorem of rays
- Angles explained to students. mathematik-wissen.de











![[BA]](https://wikimedia.org/api/rest_v1/media/math/render/svg/28e56d00eabfbd70f8db2b8c78f8f536bce7d87b)
![[BC]](https://wikimedia.org/api/rest_v1/media/math/render/svg/fd2ee765006b05ac0001c01a206871306f108cbc)