percent
| Auxiliary unit of measure | |
|---|---|
| Unit name | percent |
| Unit symbol | |
| Formula symbol | |
| Type | quotient |
| definition | |
| Named after | Italian per cento , "for a hundred, from a hundred" |
| See also: per mille , ppm , ppb | |
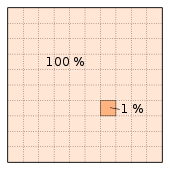
Figures in percent ( lat .- ital . Of hundreds, hundredths ) should proportions illustrate and make them comparable by the sizes are set to a uniform basic value (hundred) into consideration. The percent is therefore also used as an auxiliary unit of measurement for proportions . Older legal texts in particular use the expression “ by the hundred ” (abbreviated: vH or v. H. ); The DIN recommends, however, to avoid this expression.
Percentages are indicated by the percentage sign % (for example 63.7%). According to DIN 5008 , a space is placed between the number and the percentage sign . The percentage calculation can then be carried out as a fraction calculation (19% = 19/100) or in the decimal system (19% = 0.19).
definition
The percent sign can be mathematically as digit Postfix - operator define the standing in front of the Prozentfuß (also percentage given) divides by 100, and thus it the associated percentage assigns. It is defined by a linear function that maps the real numbers into the real numbers :
Examples:
- One percent is one hundredth:
- One hundred percent are a whole:
- 75 percent are three quarters:
- 50 percent are half:
Terms
Percentages describe proportions and relate to a basic value . The base value is the output variable to which the percentage refers. The percentage foot indicates how many hundredths of the basic value the percentage is and thus denotes a size ratio relative to the basic value. The absolute determination of this quantity is called a percentage . The percentage value has the same unit as the basic value. It applies
Example:
The term percentage is used differently in the literature. Some authors use it for expression , others use it for expression . Some authors use the terms percentage feet for the term and percentage for the term for the sake of better distinction .
understanding
Percentages express quantitative proportions and fulfill the same function as the formulations “a half” or “a quarter”. "Half a thing" means the same as "50 percent" and "a quarter" means the same as "25 percent". Percentages can also express finer proportions than the formulations commonly used in everyday language , for example “23 percent”, which corresponds to 23 hundredths of a basic value.
Just like “a half” or “a quarter”, a percentage expresses a relationship to a basic value : a half of which basic value? = 50 percent of which basic value?
The meaning of the terms "around" and "on" must be distinguished:
- “My salary has increased by 5 percent” means the same as “My salary has increased to 105 percent”.
- “The rent has fallen by 3 percent” means the same thing as “The rent has dropped to 97 percent”.
- For comparison : "Consumption has fallen by a quarter" means the same as "Consumption has fallen to three quarters of previous consumption".
If you compare percentage values, you can express this in percentage points or as a percentage of the starting percentage . Example: The election result of a party increases from 4% to 5%. The party improves by 1 percentage point, or 25% (to 125% of the starting percentage). Percentage points are the simple difference between two percentages. However, if the difference is expressed in percent (of the starting percentage), then the starting percentage must be set to 100%. In the example above, 5% equals 125% of 4%.
Conversion between number and percentage
Convert percentage to number
The percent symbol % can be replaced by its equivalent “ ”. Example:
- 50% is the same as so or reduced fraction
Convert number to percentage
Multiply the fraction by 100% (which is the same as 1). Example:
Variants of the percentage calculation
The percentage calculation is carried out and taught in different ways depending on the requirements and requirements. In this way, the usual formulas can be obtained with proportions, which saves them from having to remember. In so-called mental arithmetic, the mediating question is usually what 100% or 1% is (corresponds to).
Example:
42 kg is 7%. How much is (corresponds to) 100%?
Are given W (percentage) and p % (percentage).
We are looking for G (basic value).
|
With a general formula |
With its own ratio equation ( proportion ) |
With "What is 1%?" ( Rule of three )
|
|---|---|---|
|
multiple switching results in: |
simple repositioning results in: |
without changing the last counter gives: |
| Advantage: • One formula for all tasks |
Advantages: • Without a formula • Easy to change if the required variable - here G - is in the counter at the top left. |
Advantages: • Without a formula • Simple rule of three - here as a chain of equations • Use in mental arithmetic |
Examples
Proportion calculation
We use the abbreviations introduced above:
- Base value G : The output variable (which corresponds to 100%)
- Percentage value W : The proportional value, derived from the base value as a percentage.
- Percentage p% : The proportion of W in G , expressed as a percentage
- Percentage foot p : The number before the percent sign.
The basic formula for the percentage as the ratio of percentage value and basic value is thus:
- .
For the percentage foot instead of the percentage, the formula takes the following form:
- .
Depending on the intended use, the basic formula can also be resolved according to the basic value G or the percentage value W :
and
- .
example
If 42 kg is exactly 7%, what weight is the full 100%?
The following sizes are known here:
- Percentage W : 42 kg
- Percentage p% : 7%.
The basic value G is sought .
The solution results from the basic percentage formula resolved according to G as
- .
value added tax
A common example is the calculation of sales tax . This is defined by the value of a product ( net amount ) multiplied by a sales tax rate , which is given as a percentage. The basic value of this percentage is therefore the net amount. The gross amount is the sum of the net amount and sales tax:
- Sales tax = net amount · sales tax rate
- Gross amount = net amount + sales tax
If the net amount is 100 euros and the sales tax rate is 19%, the sales tax is calculated as follows:
- 100 euros 19% = 100 euros 0.19 = 19 euros
As a result, the gross amount is calculated as follows:
- 100 euros + 19 euros = 119 euros
Substituting it into the formula one gets:
- Gross amount = net amount + sales tax
- Gross amount = net amount + (net amount · sales tax rate)
- Gross amount = net amount (1 + sales tax rate)
In the example given with a sales tax rate of 19%, you get
- Gross amount = net amount (1 + 19%) = net amount (1 + 0.19) = net amount 1.19
By changing this formula, the net amount can easily be calculated from the gross amount
The sales tax included in the gross amount is
Use of language
In common parlance, when specifying percentages, the mathematical definition is often ignored, which is the cause of inaccuracies and errors. Examples are:
- "The invoice amount includes 19% sales tax"
- means that the sales tax rate is 19% and the invoice amount is the gross amount, i.e. the net amount plus sales tax. It should therefore read correctly: “The invoice amount includes sales tax at a sales tax rate of 19%”.
- "The sales tax is 19%"
- Wrong, it should actually mean “the sales tax rate is 19%”.
- "19% of the invoice amount is sales tax"
- Wrong, because the invoice amount is the net value plus sales tax. For example, 19% of an amount of 119 euros corresponds to 22.61 euros. In fact, the sales tax included is 19 euros and makes up around 15.97% of the invoice amount.
- Since 19% and 15.97% are not far apart, the wrong formulation can lead to unnoticed errors. Therefore the following examples:
- "My pocket money has increased by 50%."
- If the pocket money after the increase is a total of 15 euros, 50% here corresponds to 5 euros. “50%” refers to the basic value of 10 euros. This is the amount of pocket money before the increase.
- "50% of my pocket money is a grant from my grandma."
- If the pocket money amounts to a total of 15 euros, 50% corresponds to 7.50 euros. "50%" refers to the basic value of 15 euros. Although the percentage “50%” is the same in both statements, the percentages “5 euros” and “7.50 euros” are different because the statements refer to different basic values.
Incline in percent
In technology (e.g. pipelines), the gradient (or the gradient) is also given in percent. This percentage expresses the relationship between the height difference and the horizontal distance. A slope of 100% therefore means a slope angle of 45 °. A gradient of 10% means that a height difference of 10 m is covered on a horizontal distance of 100 m.
In road traffic , the value given on a traffic sign does not indicate the average gradient of the entire route, but rather the maximum gradient that acts on the wheelbase of a motor vehicle covering the route.
Mathematically, a slope in percent can be converted into an angle using the arctangent function (in degrees , rad or gon, depending on the DRG setting of the calculator ):
The following table shows some typical values for railway lines (range around 1%), mountain roads (range between 10% and 30%), ski slopes (range up to 100%) and some extreme values for illustration.
| pitch | Angle (approx.) |
|---|---|
| 0 ‰ (= 0.0%) | 0.0 ° |
| 1 ‰ (= 0.1%) | 0.057 ° |
| 3 ‰ (= 0.3%) | 0.17 ° |
| 1 % | 0.57 ° |
| 3% | 1.72 ° |
| 8th % | 4.57 ° |
| 10% | 5.71 ° |
| 12% | 6.84 ° |
| 15% | 8.53 ° |
| 20% | 11.3 ° |
| 25% | 14.0 ° |
| 30% | 16.7 ° |
| 40% | 21.8 ° |
| 50% | 26.6 ° |
| 70% | 35.0 ° |
| 100% | 45.0 ° |
| 200% | 63.4 ° |
| 500% | 78.7 ° |
| 1000% | 84.3 ° |
| 10000% | 89.4 ° |
| ∞ (infinite)% | 90.0 ° |
Mixtures of substances
It should also be noted that percentages for the content of a substance can be given as a ratio of grams per 100 grams, whereby it must be specified and differentiated whether (as with solubility data) grams of substance are meant per 100 g of the solvent or grams of substance per 100 grams of a finished solution (in the sense of an indication of the concentration ) (for more information, see content information ).
In the case of percentages of substance mixtures, it must be stated whether this relates to the mass fraction or the volume fraction . If the substances have different densities , these two statements are different. For example, the alcohol content of beverages is given in percent by volume ( % vol. ).
Since alcohol has a lower density (approx. 0.8 g / cm³) than water (approx. 1 g / cm³), the proportion of alcohol in percent by weight is lower than that in percent by volume. For example, for a drink with 50% alcohol by volume, the proportion by mass of the alcohol is only 44.4% (mass).
Input on the calculator
Pocket calculators of different designs and manufacturers treat the keyboard input of a percentage calculation differently. This can lead to confusion or to the fact that users of pocket calculators do without the percent key for percentage calculations and rather use the rule of three or the above formula.
etymology
The term percent comes from the merchant language and first appeared in German in the 15th century in commercial documents from southern Germany. However, the current word is not used there, but rather the per cento ( German per hundred) taken from Italian . The Italian cento, in turn, is derived from the Latin centum (German one hundred ). In the 16th century, a change to per cento prevailed in the High German-speaking area , which has then become today's percent and the now outdated relatinized form per centum . In Austria, however, the original Italian form was retained and became the current (but now outdated) percent .
Notation
- The typographically correct spelling is with a space between the number and the percentage sign. A non-breaking space is to be used here in the computer sentence to prevent a break between number and percent sign.
- This rule applies in addition to German in many other languages such as French, Norwegian, Russian and Swedish. In the English language, however, there is no space between the number and the percentage sign.
- When used with a suffix, it is written together. Example: "15% gradient". It is more elegant, however, to spell out half or fully: “15 percent gradient” or “fifteen percent gradient”.
- Singular / Plural: 1% is written in the singular, preferably with “a” instead of a number: “That is only one percent of all votes”. Other values in the plural: "That is 7.5% of the vote." Or "That is only three percent of the vote."
More terms
- Percentage ranks or percentiles denote the intervals that break a statistical distribution down into 100 proportionally equal parts.
- Per mille have 1000 as a reference value, not 100.
- Hundreds of a percent are referred to as basis points for interest rates.
- The term braking percentage is used in railways to indicate the braking capacity of rail vehicles.
Web links
- Formula collection math: Percentage calculation - Clear presentation of the most important formulas for percentage calculation
- Percentage calculation with formulas . In: Serlo .
Individual evidence
- ↑ Meyer's large pocket dictionary in 24 volumes . BI-Taschenbuchverlag 1992, Volume 17, p. 308.
- ^ Society for German Language: Occurrence of X of the Hundred Retrieved on November 21, 2012.
- ↑ Point 3.1.5, Table 2 in DIN 1333 - September 1992 edition.
- ↑ a b Jürgen Tietze: Introduction to financial mathematics . 10th edition, Vieweg + Teubner Verlag 2010, ISBN 978-3-8348-9643-8 , pp. 1–2 ( excerpt (Google) ).
- ↑ Meyers kleine Enzyklopädie Mathematik, Mannheim: Meyers Lexikonverl., 1995, 14., revised. and exp. Ed. / Ed. by Siegfried Gottwald… ISBN 3-411-07771-9 ; P. 149.
- ^ Fritz Reinhardt: dtv-Atlas Schulmathematik . Deutscher Taschenbuch Verlag 2002, ISBN 3-423-03099-2 , pp. 90–91.
- ↑ a b c Etymology. Dictionary of origin of the German language . Duden Volume 7, Bibliographisches Institut Mannheim 1963, ISBN 3-411-00907-1 , p. 535.
- ↑ http://www.duden.de/definition/pro%20centum
- ↑ Boris Paraschkewow: Words and names of the same origin and structure: Lexicon of etymological duplicates in German . Walter de Gruyter 2004, ISBN 978-3-11-017470-0 , p. 54 ( excerpt in the Google book search).
- ↑ http://www.duden.de/definition/perzent (accessed December 5, 2009)