One-digit link

A one- digit link (also unary or monadic link) is a link with only one operand in mathematics . A simple example of a one-digit combination is the unary minus to form the opposite of a number. One-digit links are usually viewed as functions on a given set . They are used in algebra , logic and computer science , among others .

definition

A one-digit link on a set is a self-mapping ${\displaystyle \alpha }$ ${\displaystyle A}$

${\displaystyle \alpha \colon A\to A,\quad a\mapsto \alpha (a)}$.

The pair is then also called single-digit algebra or chain . The one-digit link is the associated structure mapping. ${\displaystyle (A,\alpha )}$ ${\displaystyle \alpha \colon A\rightarrow A}$

notation

One-digit links are noted in different ways.

• The quotation as a function. This is the name commonly used in mathematics. The function sign precedes the argument to which the function is applied. For example: . If it is clear what the function sign and what the argument is, you can do without brackets. This is the case, for example, with the root function. ${\displaystyle {\sqrt {x}},\sin(x),\log(x),\exp(x)}$
• The prefix notation . This is actually nothing different from the function notation described above. The function sign precedes the argument. In some programming languages ​​this is done consistently. For example in Lisp .
• The postfix notation . The function sign is behind the argument.
• The use of diacritics .

Examples

Examples of single-digit links are:

• ${\displaystyle -x}$(Negation, formation of the opposite number of a number ). This is an example of prefix notation. ${\displaystyle x}$
• ${\displaystyle n!}$( Factorial of a natural number ). This is an example of Postfix notation. ${\displaystyle n}$
• ${\displaystyle x^{2}}$( Squaring a real number ) ${\displaystyle x}$
• ${\displaystyle {\overline {z}}}$: If the set of complex numbers, the function is a one-digit combination of . The function value of is called. ( Conjugation of a complex number ). This is an example of the use of diacritical marks. ${\displaystyle \mathbb {C} }$ ${\displaystyle \mathbb {C} \ni a+b\cdot i\mapsto a-b\cdot i\in \mathbb {C} }$ ${\displaystyle \mathbb {C} }$ ${\displaystyle z}$ ${\displaystyle {\overline {z}}}$ ${\displaystyle z}$

history

Richard Dedekind , in his paper from 1887 "What are and what should the numbers" examine quantities together with a self-mapping . So, using the language of this article, he is examining sets with a one-digit association. He calls a lot a system. A subset for which he calls a chain . is therefore complete compared to the operation . The crowd is itself a chain. ${\displaystyle A}$ ${\displaystyle \alpha \colon A\rightarrow A}$ ${\displaystyle K\subset A}$ ${\displaystyle \alpha (K)\subset K}$ ${\displaystyle K}$ ${\displaystyle \alpha }$ ${\displaystyle A}$

Perhaps Dedekind had the following idea when he chose the name chain. If you start at and apply the self-mapping over and over again , you get a track or chain. ${\displaystyle a\in A}$ ${\displaystyle \alpha }$

${\displaystyle a\rightarrow \alpha (a)\rightarrow \alpha (\alpha (a))\rightarrow \dots }$

In order to examine these chains he developed a considerable part of today's multilingual language. This is how he explains what intersection and union of sets is. Each subset is contained in a smallest sub-chain of . This is the substring of created by . The principle of complete induction now says: Together with the one-digit link, let it be a chain generated by the subset . To show that every element has a property , it must be shown: ${\displaystyle U\subset A}$ ${\displaystyle A}$ ${\displaystyle U}$ ${\displaystyle A}$ ${\displaystyle A}$ ${\displaystyle \alpha }$ ${\displaystyle U}$ ${\displaystyle {\mathfrak {E}}}$ ${\displaystyle A}$

1. Every element from has this property. ${\displaystyle U}$
2. The set of all elements with the property is closed with respect to one another. ${\displaystyle {\mathfrak {E}}}$ ${\displaystyle \alpha }$

Up to this point there is no special property of the natural numbers.

He elegantly defines what an infinite amount is. A set is called infinite if there is an injective but not a surjective function . From the existence of an infinite set he then deduces the existence of the set of natural numbers with the operations . Peano took up this a short time later. ${\displaystyle A}$ ${\displaystyle \alpha \colon A\rightarrow A}$ ${\displaystyle +,\cdot }$

use

In algebra , one-digit links are often used when defining algebraic structures . A group is defined as a tuple consisting of a carrier set , a two-digit link , a one- element (this is a zero-digit link ) and a single-digit link that assigns the associated inverse element to a group element . ${\displaystyle (G,\cdot ,1,{}^{-1})}$ ${\displaystyle G}$ ${\displaystyle \cdot }$ ${\displaystyle 1}$ ${\displaystyle {}^{-1}}$

In logic , the negation of a statement is an important one-digit association. ${\displaystyle \neg a}$ ${\displaystyle a}$

In programming languages , a number of single-digit links are often provided as ready-made functions. Examples in the C programming language are:

• Sign : +a,-a
• Increment : a++,++a
• Decrement : a--,--a
• Bitwise complement :~a
• Logical negation :!a
• Referencing :&a
• Dereferencing :*a

Lower chains

• A subset of the chain is called a sub-chain of if it is closed opposite . That is . ${\displaystyle U\subset A}$ ${\displaystyle (A,\alpha )}$ ${\displaystyle A}$ ${\displaystyle \alpha }$ ${\displaystyle \alpha (U)\subset U}$
• The intersection and union of sub-chains is a sub-chain.
• Each subset is contained in a smallest subchain of , which contains. It is called the sub-chain created by and is referred to in this article with . For the substring created by this element is also written briefly instead of . ${\displaystyle U\subset A}$ ${\displaystyle A}$ ${\displaystyle U}$ ${\displaystyle U}$ ${\displaystyle [U]}$ ${\displaystyle a\in A}$ ${\displaystyle [a]}$ ${\displaystyle [\{a\}]}$
• Is there in the chain such that , it is said: is generated by an element. ${\displaystyle a\in A}$ ${\displaystyle A=[a]}$ ${\displaystyle A}$

Morphisms

If there are chains with the structural mappings, then a map is called a morphism if it applies. ${\displaystyle (A,\alpha ),(B,\beta )}$ ${\displaystyle \alpha ,\beta }$ ${\displaystyle f\colon A\rightarrow B}$ ${\displaystyle f\circ \alpha =\beta \circ f}$

• Identity is always a morphism. ${\displaystyle A\ni a\mapsto a\in A}$
• If there are chains and morphisms, then there is a morphism. ${\displaystyle (A,\alpha ),(B,\beta ),(C,\gamma )}$ ${\displaystyle f\colon A\rightarrow B,g\colon B\rightarrow C}$ ${\displaystyle g\circ f\colon A\rightarrow C}$

One says the class of the chains together with the morphisms form a category. In the book by F. William Lawvere and Stephen H. Schanuel "Conceptual Mathematics" this is called the category of endomaps. In this article it will be referred to as the category of chains.

In the picture we have the chain and the structure map . In addition, the chain with the structure illustration . If you go one step further in the top line and then click over , you get the same thing as if you first translate with and then continue with . The pattern repeats itself from the pair onwards . You can see there is exactly one second morphism . And the morphism with . ${\displaystyle A=\{a_{0},a_{1},a_{2},a_{3},a_{4},a_{5}\}}$ ${\displaystyle \alpha \colon a_{0}\mapsto a_{1}\mapsto a_{2}\mapsto a_{3}\mapsto a_{4}\mapsto a_{5}\mapsto a_{0}}$ ${\displaystyle B=\{b_{0},b_{1}\}}$ ${\displaystyle \beta \colon b_{0}\mapsto b_{1}\mapsto b_{0}}$ ${\displaystyle \alpha }$ ${\displaystyle f}$ ${\displaystyle B}$ ${\displaystyle f}$ ${\displaystyle \beta }$ ${\displaystyle (a_{5},b_{1})}$ ${\displaystyle A\rightarrow B}$ ${\displaystyle g(a_{0})=b_{1}}$

• Two chains are called isomorphic if there is a morphism that is bijective as a mapping. The inverse mapping is then also a morphism. ${\displaystyle A,B}$ ${\displaystyle A\rightarrow B}$

Dedekind's recursion theorem

Simply infinite amount

A chain with an injective is simply called infinite , if there is one with and it is . It is by generated. With these terms applies: ${\displaystyle (A,\alpha )}$ ${\displaystyle \alpha }$ ${\displaystyle a\in A}$ ${\displaystyle a\notin \alpha (A)}$ ${\displaystyle [a]=A}$ ${\displaystyle A}$ ${\displaystyle a}$

Theorem : The following statements are equivalent:

1. There is a simplest infinite set.
2. There is a chain and such that the Peano axioms are fulfilled. These are: ${\displaystyle (A,\alpha )}$ ${\displaystyle a\in A}$
   1. ${\displaystyle a\notin \alpha (A)}$.
   2. ${\displaystyle \alpha }$ is injective.
   3. Every subset completed opposite , with is already the same . ${\displaystyle \alpha }$ ${\displaystyle X\subset A}$ ${\displaystyle a\in X}$ ${\displaystyle A}$

Note: This formulation is mainly from Richard Dedekind. If you look under the term Peano axioms , they are a little different.

• But 1. and 2. of the formulation there is called is a chain. ${\displaystyle (A,\alpha )}$
• 3. stated in the wording there . ${\displaystyle a\notin \alpha (A)}$
• 4. states that is injective. ${\displaystyle \alpha }$
• 5. the formulation there is our statement 3.

If you choose the above formulation, it is initially still completely unclear whether there are not essentially different simply infinite sets. For example, choose a rotation around a certain angle as the plane and as the structure mapping. ${\displaystyle A}$

Recursion sentence

Sentence: (Dedekind recursion sentence 1887)

If the set is simply infinite, then: ${\displaystyle (A,\alpha )=([a],\alpha )}$

For every chain and every there is exactly one morphism with . ${\displaystyle (B,\beta )}$ ${\displaystyle b\in B}$ ${\displaystyle f\colon A\rightarrow B}$ ${\displaystyle f(a)=b}$

Conclusion: Any two simply infinite chains are isomorphic. That is, there is isomorphism between the chains. They are especially equally powerful as sets.

Algebraic structure of natural numbers

The addition

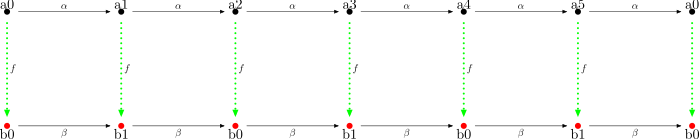
One chooses a simply infinite set and calls it N. The structure map should be denoted by 1+. The generating element hot 0. Then can be defined with the Recursion Theorem: For every there is exactly one morphism with . Look at the drawing. ${\displaystyle a\in N}$ ${\displaystyle \sigma (a,-):N\times N\ni (a,x)\mapsto \sigma (a,x)\in N}$ ${\displaystyle \sigma (a,0)=a}$

Basically, it's the addition of two numbers with the help of meter sticks. You put two meter sticks on top of each other and move the upper one by a. If you want to find out what is, read under b - where the green arrow points - on the lower meter stick. ${\displaystyle \sigma (a,b)}$

The following theorem applies:

Sentence: The figure defined above has the following properties.

1. For everyone is . So the image is the identity. ${\displaystyle a\in N}$ ${\displaystyle \sigma (0,a)=a}$ ${\displaystyle \sigma (0,-)}$
2. For everyone is . ${\displaystyle a,b,c\in N}$ ${\displaystyle \sigma (\sigma (a,b),c)=\sigma (a,\sigma (b,c))}$
3. For everyone is . ${\displaystyle a,b\in N}$ ${\displaystyle \sigma (a,b)=\sigma (b,a)}$
4. The following applies to everyone : is , so is . ${\displaystyle a,b,c\in N}$ ${\displaystyle \sigma (a,b)=\sigma (a,c)}$ ${\displaystyle a=b}$

The symbol should remind of sum. And so the sentence becomes more familiar if we use the usual character and put it between the arguments. ${\displaystyle \sigma }$

Sentence: The figure has the following properties. ${\displaystyle +\colon \mathbb {N} \times \mathbb {N} \rightarrow \mathbb {N} }$

1. For everyone is . ${\displaystyle a\in \mathbb {N} }$ ${\displaystyle 0+a=a}$
2. For all is . ${\displaystyle a,b,c\in \mathbb {N} }$ ${\displaystyle (a+b)+c=a+(b+c)}$
3. For all is . ${\displaystyle a,b\in \mathbb {N} }$ ${\displaystyle a+b=b+a}$
4. The following applies to everyone : is , so is . ${\displaystyle a,b,c\in \mathbb {N} }$ ${\displaystyle a+b=a+c}$ ${\displaystyle b=c}$

The second formulation has the advantage of familiarity. It has the disadvantage that it hides the freedoms that one still has. The first formulation applies to any simply infinite amount. Also on one with a completely different structure mapping.

In summary one says: is a commutative regular monoid ${\displaystyle (\mathbb {N} ,+)}$

The multiplication

We now write the usual character between the arguments. So instead of . The image ${\displaystyle +}$ ${\displaystyle a+b}$ ${\displaystyle \sigma (a,b)}$

${\displaystyle a+\colon \mathbb {N} \ni b\mapsto a+b\in \mathbb {N} }$makes a chain . ${\displaystyle \mathbb {N} }$ ${\displaystyle (\mathbb {N} ,a+)}$

The multiplication by 2 is shown in an arrow diagram

Therefore there is exactly one morphism with . It is then . And it is . We see exactly what is naively meant by multiplying by a number . is added to itself. If we write for , then the following theorem applies: ${\displaystyle m(a,-)\colon (\mathbb {N} ,1+)\rightarrow (\mathbb {N} ,a+)}$ ${\displaystyle m(a,0)=0}$ ${\displaystyle m(a,1)=m(a,1+0)=a+m(a,0)=a}$ ${\displaystyle m(a,2)=m(a,1+1)=a+m(a,1)=a+a}$ ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle m(a,b)=a\cdot b}$

Sentence:

1. ${\displaystyle 0\cdot b=0}$for everyone . ${\displaystyle b\in \mathbb {N} }$
2. ${\displaystyle 1\cdot b=b}$for everyone . ${\displaystyle b\in \mathbb {N} }$
3. ${\displaystyle a\cdot (b+c)=a\cdot b+a\cdot c}$for everyone . ${\displaystyle a,b,c\in \mathbb {N} }$
4. ${\displaystyle (a+b)\cdot c=a\cdot c+b\cdot c}$for everyone . ${\displaystyle a,b,c\in \mathbb {N} }$
5. ${\displaystyle a\cdot b=b\cdot a}$for everyone . ${\displaystyle a,b\in \mathbb {N} }$
6. ${\displaystyle (a\cdot b)\cdot c=a\cdot (b\cdot c)}$for everyone . ${\displaystyle a,b,c\in \mathbb {N} }$
7. Is , so is or . ${\displaystyle a\cdot b=0}$ ${\displaystyle a=0}$ ${\displaystyle b=0}$

Properties 1) to 6) are summarized when one says is a commutative half-ring with a neutral element . This is the most important half-ring of all. These procedures can be continued and this is how exposure occurs . Note that the natural numbers were never used as cardinal numbers in the whole construction. It's the pure counting numbers. But not counting in the sense of counting the number of a set, but simply in the sense of reciting the numerals in an orderly manner. ${\displaystyle (\mathbb {N} ,+,\cdot )}$ ${\displaystyle 1}$ ${\displaystyle \dots }$

See also

• Arity
• Unary system

literature

• Richard Dedekind: What are and what are the numbers . Vieweg, 1965.
• Hartmut Ernst: Basic course in computer science . Springer, 2013, ISBN 978-3-322-91968-7 , pp. 266 .
• Ulrich Knauer, Kolja Knauer: Discrete and Algebraic Structures - In Brief . Springer, 2015, ISBN 978-3-662-45177-9 , pp. 141 .
• F. William Lawvere, Stephan H. Schanuel: Conceptual Mathematics A first introduction to categories . 2009, ISBN 978-0-521-71916-2 .

Individual evidence

1. ↑ Richard Dedekind "What are and what are the numbers"
2. ↑ See the book by F, William Lawvere, and Stephen H. Schanuel

Web links

• http://www.opera-platonis.de/dedekind/Dedekind_Zahlen.html
• Algebraic operation . In: Michiel Hazewinkel (Ed.): Encyclopaedia of Mathematics . Springer-Verlag , Berlin 2002, ISBN 978-1-55608-010-4 (English, [ Algebraic operation ( Memento of November 3, 2012 in the Internet Archive ) online]).
• Matt Insall: Unary Operation . In: MathWorld (English).