Self-mapping

An image that depicts a lot in itself is called self-image in mathematics . These mappings play an important role in all branches of mathematics: On the one hand, information about this structure can be obtained through the changes that the structure of the set undergoes during self-mapping, on the other hand, an element and its picture element can be compared directly with one another, since the mapping does not lead out of its domain and can be applied repeatedly.

The first concept of describing structures through their structurally true or structurally compatible self-mapping was first introduced into geometry by Felix Klein's Erlangen program and is one of the most fruitful ideas in modern mathematics. The second concept, which is based on the comparability of archetypes and images as well as the iterability of self-mapping, is indispensable for numerics and is one of the fundamental concepts of fractal geometry .

definition

Be any set. Then a function is called a self-mapping. is a one-digit shortcut on . ${\displaystyle A}$ ${\displaystyle \alpha \colon A\to A}$ ${\displaystyle \alpha }$ ${\displaystyle A}$

Examples

1. The identity on a crowd is a self-image. . ${\displaystyle A}$ ${\displaystyle id_{A}\colon A\to A;\ a\mapsto a}$
2. The most important example of a self-mapped crowd is counting. Every natural number is assigned its successor . . ${\displaystyle 1+\colon \mathbb {N} \to \mathbb {N} ;\ n\mapsto 1+n}$
3. If a number is shown in the decimal system, you can assign its cross sum to it. So is about . General . It is divisible by 3 if and only if is divisible by 3. ${\displaystyle n}$ ${\displaystyle q(n)}$ ${\displaystyle q(12345)=15,q(15)=6}$ ${\displaystyle \textstyle q\colon \mathbb {N} \to \mathbb {N} ;\ \sum _{i=0}^{k}a_{i}\cdot 10^{i}\mapsto \sum _{i=0}^{k}a_{i}}$ ${\displaystyle n}$ ${\displaystyle q(n)}$
4. Let it be the set of positive rational numbers and a self-mapping. If one applies repeatedly and assumes, for example , the result is obtained . As a result of these fractions, the numerator and denominator are consecutive Fibonacci numbers . In this sequence has the limit value . This is the golden section number . ${\displaystyle \mathbb {Q} ^{+}}$ ${\displaystyle \alpha \colon \mathbb {Q} ^{+}\to \mathbb {Q} ^{+};\ x\mapsto {\tfrac {1+x}{x}}}$ ${\displaystyle \alpha }$ ${\displaystyle x=1}$ ${\displaystyle 1\mapsto 2\mapsto {\tfrac {3}{2}}\mapsto {\tfrac {5}{3}}\mapsto {\tfrac {8}{5}}\mapsto \dotso }$ ${\displaystyle \mathbb {R} }$ ${\displaystyle \Phi ={\tfrac {1+{\sqrt {5}}}{2}}}$

Structure-preserving self-mapping

Endomorphisms and automorphisms

A structure-compatible self-mapping is structure-preserving and is called endomorphism . If this mapping is also reversible and its inverse mapping is also structure-preserving, then it is called an automorphism . The structure that is retained in these illustrations can be very different in different mathematical sub-areas. In algebra, it is usually sufficient to require that the mapping itself is structure-preserving and reversible, which means that the inverse mapping is also structure-preserving .

Structure description through automorphisms and invariants

A very general structure is assumed, for example a vector space V. This gives a basic set of automorphisms which, as reversible mappings, form a group - in the example the automorphism group - which respect the vector space structure. Additional structures such as spacing or angles are now introduced. The requirement that one or more of these structures may be invariant under automorphisms characterizes a subgroup in the original group . The Erlangen program now provides for each “geometry” (understood as a system of invariants) to be described by subgroups and, conversely, subgroups of the full automorphism group by their invariants.

In theoretical physics , the basic idea is used to infer conservation laws (invariants) from the symmetries of a problem (group).

iteration

The concept of continuously applying one and the same self-mapping to an element or a set is used on the one hand to obtain approximations for fixed points of the mapping through iteration , on the other hand to define certain classes of sets such as grids and fractals - for example in geometry .

Iterative approximation methods

A special case from real analysis is described in contraction (mathematics) . A generalization is the Banach Fixed Point Theorem .

Definition of "iterative sets"

Formally, as with the Erlangen program, this is again about invariants, but these definitions usually occur outside of classical geometric relationships.

Periodic figures

A figure in the plane is called periodic if it is mapped onto itself by a shift . Periodic figures are, for example, the graphs of the trigonometric functions sine, cosine, ... Lattices are also periodic figures. The corresponding definition can be transferred without difficulty to vector spaces of any dimension. ${\displaystyle F}$

Fractal sets

Fractal sets are self-similar sets, i.e. subsets of a real or complex vector space , which are mapped onto themselves through a similarity mapping. Here the self-mapping is therefore (in the finite-dimensional case) a rotation extension.

An example of use

Logistic illustration bifurcation diagram. The accumulation points x are plotted as a function of the value of the parameter r .

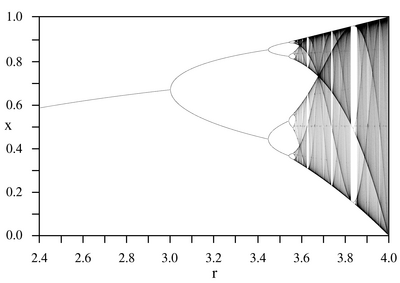
Self-mapping play an important role in the study of dynamic systems . The logistic mapping can serve as an example for many applications: ${\displaystyle \varphi }$

${\displaystyle \varphi (x)=rx(1-x)}$

With

${\displaystyle 0\leq x\leq 1}$

and

${\displaystyle 0\leq r\leq 4}$

The graphic shows the accumulation points of the

${\displaystyle x_{n+1}=\varphi (x_{n})}$

recursively defined sequence with ${\displaystyle 0<x_{1}<1.}$

It can be seen that the iteration sequence, depending on the value of the parameter, can be convergent or ultimately has an infinite number of accumulation points. In the area in front of the first branching, the self-mapping is contracting, its limit value is a fixed point and attractor . The diagram as a whole shows a fractal structure. ${\displaystyle r}$ ${\displaystyle \varphi }$

Individual evidence

1. ↑ Harro Heuser : Textbook of Analysis . Part 1. 17th edition. Vieweg + Teubner Verlag, 2012, ISBN 978-3-8348-0777-9 , pp. 106 .
2. ↑ Eric W. Weisstein : Self-Map . In: MathWorld (English).