Automorphism
In mathematics , an automorphism (from the Greek αὐτός autos , "self", and μορφή morphē , "shape", "form") is an isomorphism of a mathematical object on itself.
From symmetries to automorphisms
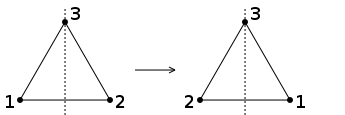
An equilateral triangle has three axes of symmetry :
It also has threefold rotational symmetry . In order to grasp the symmetry property mathematically, consider the associated symmetry mappings . The mirroring on the axis belongs to each symmetry axis:
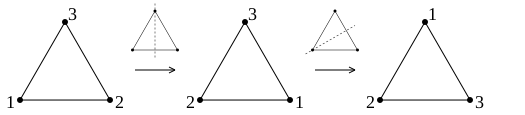
The digits are only used to describe the figure, it's the same triangle twice. Symmetry maps can be performed one after the other. In the following example, the execution of two reflections one behind the other is a rotation of 120 °:
If you carry out the same mirroring twice in succession, you get the overall image that does not change anything, the identical image . If the execution of two symmetry maps one behind the other is to be a symmetry map again, the identical mapping must be allowed. A figure is asymmetrical if it only allows this one, trivial symmetry mapping. The totality of the symmetry maps forms a group , the symmetry group .
In mathematics is often considered objects of a basic amount and an additional structure exist, and usually there is a canonical structure that from the additional structure on and a bijection a structure to generate. This is particularly possible for bijections .
Transferred to the example of symmetry corresponds to the plane and the triangle. For a congruence is the image triangle . Symmetry images are characterized by . In the abstract context, bijections that satisfy are called automorphisms of . This definition covers most cases, be it graphs , topological spaces or algebraic structures such as vector spaces .
If the additional structures become more complicated, the seemingly harmless condition can cause problems: If you define differentiable manifolds as basic sets with topology and an atlas , you may get a compatible but not identical atlas under a homeomorphism . But if one were to demand a maximum atlas in the definition, it would be for one .
The category theory solves this and other problems in that it requires an existing definition for structure compatible mappings ( morphisms ; it does not have to be actual figures act). Building on this, it replaces the requirement of bijectivity (which is no longer available in the abstract context) with the existence of an inverse morphism.
definition
Algebraic structures
Let be an algebraic structure , i.e. a set together with a (usually finite) number of (internal) links . Such an algebraic structure could be, for example, a group , a ring or a vector space (in which the links are two-digit, that is ). Then, in algebra, an automorphism is understood to be a bijective mapping of the set to itself, which is a homomorphism , that is, it applies
for each and everyone . The inverse function is then also a homomorphism.
Category theory
Be an object . A morphism is called automorphism if there is a morphism with
- and
gives, i.e. has a double-sided inverse.
An automorphism is therefore the same as
- an isomorphism whose source and destination are the same, and
- an invertible endomorphism .
For categories of algebraic structures (and their associated homomorphisms) the definition is equivalent to that in the previous section.
Automorphism group
- When the automorphisms of an object form a set, they form a group with the concatenation as a link , which is referred to as.
- If there is a group, a homomorphism is called a group operation of on .
- If a covariant functor and an object of , then induces a group homomorphism . (For contravariant functors one must still with the inversion concatenate.) Is of a group operation on given, we obtain in this way an operation of on .
Special structures
Graph
General
An automorphism of a graph with a set of nodes and a set of edges is a bijective mapping , so that applies to all .
An automorphism of a graph induces an automorphism of the complement graph .
The theorem of Frucht says that for every group there is a graph such that it is isomorphic to .
example
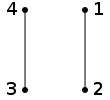
Be and :
Automorphisms of are permutations of , so applying the permutation to the diagram again yields an illustration of the same graph. Example: The permutation is an automorphism, because the edges still run between 1 and 2 and between 3 and 4:
The permutation is not an automorphism because the edges in the new image and are:
The automorphism group of the graph is isomorphic to the dihedral group of the order , its complement is a 4-cycle .
Vector spaces
An automorphism of a vector space is a bijective linear mapping .
For finite-dimensional vector spaces automorphisms are precisely those linear mappings whose mapping matrix is regular with respect to an arbitrary basis . The automorphism group is often noted as GL (V) .
groups
General
An automorphism of a group is a bijective group homomorphism of this group on itself, i.e. a bijective mapping with for all .
Under automorphisms all structural properties of the group elements as well as related constructions are preserved. Each automorphism thus preserves the order of the elements (i.e. for all ), induces an automorphism of the center and maps generating systems onto generating systems.
Inner automorphisms
Is a group and determine, then , an automorphism of , called conjugation with . Automorphisms that arise in this way are called internal automorphisms . Automorphisms that are not inner automorphisms are called outer automorphisms . Because is a homomorphism and is the trivial automorphism if and only if lies in the center of , the set of all internal automorphisms is an isomorphic subgroup of according to the homomorphism theorem . It is even a normal divisor in , and the factor group is denoted by. It is called the group of external automorphisms . The restriction to the center produces a homomorphism .
For Abelian groups all internal homomorphisms are trivial, and .
By restricting the internal automorphisms, one obtains an injective homomorphism for a subgroup . See normalizer and centralizer .
Examples
- The bijection , is accurate then a homomorphism and thus an automorphism if Abelian is.
- The group has exactly one nontrivial automorphism, namely . This follows from the fact that an automorphism maps a generating system onto a generating system.
- The automorphism group of the Klein group of four is isomorphic to the symmetric group .
- The automorphism group of the group is (by multiplication).
- The automorphism of is not an inner automorphism because its restriction to the center, the subgroup of the scalar matrices, is not trivial.
Related topics
- Subgroups that are invariant among all automorphisms are called characteristic subgroups .
body
An automorphism of a body is a bijective mapping that satisfies and for all . If there is a body extension, then those automorphisms of which satisfy for all are called the -automorphisms of . They form a group, noted or . An automorphism of is an -automorphism if and only if it is a -linear mapping.
- The conjugation for is an automorphism of the field of complex numbers .
- The mapping is for the only nontrivial automorphism of .
- The field of rational numbers and the field of real numbers have no nontrivial automorphisms. They are therefore also called rigid . As the example shows, rigidity does not transfer to the lower, upper or intermediate body. The fact that is rigid can be seen from the fact that every rational number can be represented as an algebraic expression in , whereby it must be retained as a neutral element of multiplication under automorphisms. Every automorphism on has to map every rational number to itself accordingly. Since it also maintains the order , all real numbers have to be fixed points.
- If the characteristic is a finite or general perfect field , then it is an automorphism of , the Frobenius automorphism .
- If there is a body and a subset, then there is a sub- body of , called the fixed body of . If it is a finite subgroup, then a Galois expansion is of degree . The Galois theory makes more connections between field extensions and automorphism.
Algebras
For algebras , as with groups, inner automorphisms can be defined as conjugation with a unit. Inner automorphisms are trivial on the center , and Skolem-Noether's theorem says that for a semi-simple algebra the converse is also true.
Function theory
In function theory , the morphisms are the holomorphic functions and the automorphisms are the conformal self-mapping . The automorphism group e.g. of the open unit disk is given by:
literature
- Serge Lang , algebra. Springer-Verlag 2002
Individual evidence
- ^ Albrecht Beutelspacher : Lineare Algebra . 7th edition. Vieweg + Teubner Verlag , Wiesbaden 2010, ISBN 978-3-528-66508-1 , p. 39-42 .
- ↑ Reinhard Winkler: The real numbers are different . In: Didactics booklets of the Austrian Mathematical Society . tape 41 , 2008 ( online [PDF; accessed October 13, 2014]).







































































































![\ mathbb {Q} [{\ sqrt 2}]](https://wikimedia.org/api/rest_v1/media/math/render/svg/eee5632589347f1355af6412f95e450543d1a350)






![[L: K] = | G |](https://wikimedia.org/api/rest_v1/media/math/render/svg/d4220c3f281a6e1833a33b4ab133bbbdd3ab52b2)

