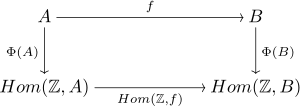|
Abelian group
|
|
|
|
This article assumes the following mathematical terms:
|
|
|
|
|
|
is a special case of
|
|
|
An Abelian group is a group for which the commutative law also applies.
The mathematical term Abelian group , also called the commutative group , generalizes arithmetic with numbers. The addition of rational numbers and the multiplication of rational numbers satisfy a number of common laws. These rules are often found in geometry and algebra. For example, with shifts, rotations of the plane around a point, addition of functions. Ornaments in art and nature trace the traces of Abelian groups. Therefore, the special meaning of the addition sign and the multiplication sign is abstracted and the concept of the commutative or Abelian group is created. The name was chosen in honor of the Norwegian mathematician Niels Henrik Abel .



definition
Be a lot . Exactly one element is assigned to each pair . The pair is called an Abelian group if the connection satisfies the following laws:





-
Associative law : For all the following applies: .


-
Commutative : For all the following applies: .


-
Neutral element : There is an element , such that for all the following applies: .



-
Inverse element : for each there is a with .



A group is called non-Abelian if at least one pair exists in it with .



Explanations
- If the commutative law is omitted from the axioms, a group results . An Abelian group is therefore nothing else than a group for which the commutative law also applies.
- The neutral element and the inverse element of each group element are clearly defined, as can be shown from the axioms.
- Usually an Abelian group is written additively with the link symbol and then called a module . In this case the sum of and , the neutral element is called zero element or simply zero and is written. The inverse of is then denoted as its opposite with .







- A commutative group can also be written multiplicatively with the link symbol. Then or is simply the product of and . In this case the neutral element is called one element or simply one and is written. The inverse of is now called .








- In a module, the difference between two elements is explained as . The rules then apply: . If the Abelian group is written multiplicatively, then the quotient is defined accordingly .



Examples
-
 is the most important Abelian group. Where is the set of whole numbers and the usual addition.
is the most important Abelian group. Where is the set of whole numbers and the usual addition.

-
 is an Abelian group. It is the set of rational numbers without and is the ordinary multiplication.
is an Abelian group. It is the set of rational numbers without and is the ordinary multiplication.


- The set of finite decimal numbers are not an Abelian group in terms of multiplication. For example, the number has no inverse with respect to multiplication. cannot be written as a finite decimal fraction. With regard to normal addition, the finite decimal fractions form an Abelian group.


- The set of displacements in the Euclidean plane form an Abelian group. The link is the sequential execution of the shifts.

A triangle around the displacement vector postponed

- The set of rotations in a plane around a point form an Abelian group. The link is the sequential execution of the rotations.
- The set of twisting stretches in a plane form an Abelian group.
- The linking table can be written down by sufficiently small groups. If it is the table of an Abelian group, the table is symmetrical to the main diagonal . This table arises, for example, if one considers the rotations of an equilateral triangle around the center of gravity, which transform the triangle into itself. is the turn around , is the turn around, and is the turn around .







- Are Abelian groups, it becomes an Abelian group through .



- Is a set and an abelian group, this is a group when it is defined . It is called the th component of . Often the form is written as a vector . It is . Is , then is the set of sequences, where the terms of the sequence are elements of . Is so is .















- The real numbers form an Abelian group with the addition; without the zero they form an Abelian group with the multiplication.
- More generally, every body yields two Abelian groups and in the same way .



- In contrast, the group of invertible matrices over a body for an example of a non- Abelian group. By the way, the smallest non- Abelian group is the symmetrical group S 3 with six elements.




Subgroups
A non-empty subset of the Abelian group is called a subgroup if it is itself a group with regard to the group operation. This is exactly the case when all the following applies: . In this article, the following notation is selected: .





-
 is a subgroup of .
is a subgroup of .
- The average of subgroups is a subgroup.
- Each subset is contained in a smallest subgroup, which contains. This subgroup is called the subgroup of created by . It is designated with .





- If there are subgroups of , then the set is a subgroup of . More generally: if a family is of subgroups, then is a subgroup of . It is called the sum of the subgroups .







- Is , then is the subgroup created by . Is that is the name of a generating system of .






- An Abelian group is said to be finitely generated if there is a finite subset such that . If it is generated by an element , it is called cyclic . It is written.







- Each subgroup of is cyclic.

- This means, for example: The sum of two cyclic subgroups of is again cyclic. It applies . Where is the
greatest common factor of . z. B. .




- Are subsets of , then is . Where is the smallest common multiple of . For example .






-
 is not finite generated. More precisely: If a generating system is and is , then there is also a generating system.
is not finite generated. More precisely: If a generating system is and is , then there is also a generating system.



- Some groups in art and nature
Fra Giovanni da Verona painted this picture as an inlay in the Sacrestia of Santa Maria in Organo. It illustrates a cyclic group of order 8 including a subgroup of order 4.
Bramante 's design for St. Peter's Basilica. Among other things, it is a fourth-order rotating group. In fact, mathematically even more is hidden in it. It's a fractal.
The flower shows the symmetry of the rotating group of the 5th order. The pentagram can also be clearly seen.
Factor groups
If it is a subgroup, it defines an equivalence relation. Are and are so is . The equivalence relation is called compatible with addition. Let be the set of equivalence classes. On is explained an addition.







-
 .
.
If we really want to calculate in, it is sufficient to limit ourselves to a system of representatives of . Because each equivalence class is uniquely determined by an element from the equivalence class. It is .



- If is a subgroup of , then is cyclic. That is, there is one with . If there is a positive representative in the equivalence class of . It is therefore not a limitation if we assume. We get a representative of by dividing with the rest. It is positive for two if and only if they leave the same remainder while dividing . It is then a system of representatives from . Denotes the radical when sharing by results, so the calculation corresponds in : the following 'addition' for . The index at the sign is omitted. So in, for example .























-
 is a subgroup of . A system of representatives of is the unit interval open to the right . In this Repräsentantesystem is expected as follows: . Where is greatest integer . It is therefore for :
is a subgroup of . A system of representatives of is the unit interval open to the right . In this Repräsentantesystem is expected as follows: . Where is greatest integer . It is therefore for :


![{\ displaystyle (a + b) {\ bmod {1}} = (a + b) - [a + b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a6bfda6fe0f4841b37d7dc970fa12da26492f6c7)
![{\ displaystyle [x]: =}](https://wikimedia.org/api/rest_v1/media/math/render/svg/206831957ac1c70e1ff5ad33a9ddd67db59ca361)



- The special properties of the subgroup of are discussed a little further below.


Homomorphisms
definition
Are Abelian groups, is an illustration homomorphism if for all applies: .




Examples of homomorphisms
- The identity and the null map are always homomorphisms. There is exactly one morphism for every Abelian group . There is exactly one homomorphism in the same way .




- If a subgroup of , the inclusion map is a homomorphism.


- The mapping is a homomorphism. General: If so, the multiplication with , i.e. the mapping , is a homomorphism. This is equivalent to distributive , which states: For all the following applies: . The multiplications are also the only homomorphisms that means: If there is a homomorphism, there is one with for all .











- If the mapping is a homomorphism, from the additive group to the multiplicative group .




- The natural exponential function : is a homomorphism of Abelian groups. It maps the additive group bijectively into the multiplicative group . The inverse mapping is the natural natural logarithm .



- The concatenation of homomorphisms is a homomorphism. The class of the Abelian groups, together with the homomorphisms, form a category (mathematics) . This is the prototype of an Abelian category .

Universal property of whole numbers
-
Each group and every there is exactly one homomorphism with . It is then , and . General is






-
 .
.
It is a free Abelian group with a base .


- It is close to and to define: . The following then applies:



-
 . (Warning! It can be confusing that the same sign is used on both sides of the equation . On the left side of the equation is the neutral element in . On the right side of the equation is the neutral element in . Both times are the different neutral elements with written.)
. (Warning! It can be confusing that the same sign is used on both sides of the equation . On the left side of the equation is the neutral element in . On the right side of the equation is the neutral element in . Both times are the different neutral elements with written.)



- For everyone is .


- For all and all is .



- For all and all is .



- For all and all is .



- In this way every module becomes a module . Is a homomorphism, then for all : .




- It is worthwhile to translate the penultimate statement for a group that is written multiplicatively. In this case the neutral element is in the . For every arbitrary there is exactly one homomorphism with . It is . General is . The above laws then say:








- For everyone is .


- For everyone is .


- For everyone is .


- For everyone is . If rational or real numbers are substituted for the set , then the laws known from school for calculating with exponents result.




Properties of homomorphisms
Is a homomorphism, and are respectively subgroups, then and are subgroups. In particular, and are subgroups. It follows from this:







- Is a group and a natural number, then and are subgroups of . This is true because multiplication by is a homomorphism.



![{\ displaystyle A [n]: = \ {a | a \ cdot n = 0 \}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ef0c387c0333813d410533184a75b54b873aeb62)


-
![{\ displaystyle T (A): = \ sum \ limits _ {n \ in \ mathbb {N}} A [n] = \ {a | a \ in A {\ text {there are}} n \ in \ mathbb {N} {\ text {with}} a \ cdot n = 0 \}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d4ad1ce0af1ee1d1aef7e5e5e47a8edb05082d45) is a subgroup of . This is the torsion subgroup of . Is , it is called torsion-free . For each group is torsion free. The torsion subgroup of is .
is a subgroup of . This is the torsion subgroup of . Is , it is called torsion-free . For each group is torsion free. The torsion subgroup of is .






- If a homomorphism is produced by elements and is produced by elements, then is produced by elements.







- Each subgroup of is generated from a maximum of elements.


Injective homomorphisms
- If there is a bijective homomorphism, the reverse mapping is also a homomorphism. In this case it is called isomorphism . Is there an isomorphism between and so called isomorphic .






- If there is a homomorphism, the following statements are equivalent. In this case it is called monomorphism .


-
 is injective as an image.
is injective as an image.
-
 .
.
- For all Abelian groups and all homomorphisms with is . It can be shortened on the left.





- The concatenation of monomorphisms is a monomorphism. That means more precisely: if monomorphisms are, then is a monomorphism.


Surjective homomorphisms
If there is a homomorphism, then the following statements are equivalent. Then it is called epimorphism .


-
 is surjective as a mapping.
is surjective as a mapping.
-
 .
.
- The following applies to all groups and everyone : is , so is . It can be shortened on the right side.





- If there is a subgroup, the mapping is an epimorphism.


- The concatenation of epimorphsms is an epimorphism. More precisely: if and are epimorphisms, then there is an epimorphism. It's called canonical epimorphism .



- If and are homomorphisms and if there is an epimorphism, then there is an epimorphism.




Isomorphism, isomorphism sentences
A bijective homomorphism is called an isomorphism . This is the case if and only if it is monomorphic and epimorphic. The following sentences apply.

-
Homomorphism theorem : be a homomorphism. the canonical epimorphism. Then there is a monomorphism with . In particular is . The following diagram is commutative .





The theorem of homomorphism applies generally to groups.
-
First isomorphism theorem : be subsets of . Then: .



-
Second isomorphism : be subgroups. Then: .


The functor Hom (A, -)
- If there are groups, the set is a group. The addition is explained by: .



- It is for every finitely generated group .


- Is the greatest common divisor of two numbers equal is so .



- For all Abelian groups is . This isomorphism is a functional isomorphism. This is explained in more detail below.


- If it is a homomorphism, the assignment is a homomorphism. For the following applies: . If the identity is up , then the identity is up . If there is an isomorphism, then there is an isomorphism. Becomes










- Each Abelian group has the Abelian group and


- assigned the homomorphism to each homomorphism , one obtains the functor from the category of the Abelian groups into the category .





- The last statement sheds light on the universal property of . Since it to each one uniquely determined homomorphism with are, the assignment is a function. More precisely , the following applies: The map family: has the following property: For all and all homomorphisms is . In addition, the mapping is an isomorphism for all of them . The inverse map is . That is, the following diagram is commutative for all and all with isomorphisms .














 That means, among other things , monomorphism or epimorphism is exactly when it is.
That means, among other things , monomorphism or epimorphism is exactly when it is.

-
Hom (G, -) and exact sequences: If an exact sequence is an exact sequence of Abelian groups, then the induced sequence for each group is exact. It is . The functor is called exact on the left . If there is an epimorphism, there is usually no epimorphism.







- The following laws apply to.

- For everyone is and .



- For everyone is and .



- For everyone is . is a unitary ring .



Generalizations, going on
The theory of Abelian groups is rich. Some basic terms should be pointed out here. Sometimes there is an entry in Wikipedia for a partial aspect. Usually not.
- Each module is a module above the ring (see above ). If we replace it with any ring , we get a module. Sentences about Abelian groups can often be transferred to modules about main ideal areas. An example is the classification of finitely generated Abelian groups (see below).




-
Torsion groups : A torsion element is called if there is a natural number such that . The set of all torsion elements in a group form a subgroup. For example, the torsion subgroup is from .





-
Direct sums of Abelian groups : The term is explained here for the case of two subgroups . Is and is called the direct sum of .





- Direct product.
-
free abelian group : some abelian groups have something like a base in a vector space. In the theory of modules, the free modules play a major role.

- Divisible Abelian group
-
finally generated Abelian group . Their structure is pretty much clear. They are the direct sum of indecomposable cyclic groups.
- For any Abelian group, analogous to the concept of the dimension of a vector space, each Abelian group can be assigned its rank . It is defined as the greatest thickness of a -linearly independent subset. The integers and the rational numbers have rank 1, as do every subgroup of . The Abelian groups of rank 1 are well understood, but there are still many questions unanswered for higher ranks. Abelian groups of infinite rank can be extremely complex and their open questions are often closely related to questions of set theory .



literature
-
Siegfried Bosch : Algebra. 7th, revised edition. Springer, Berlin a. a. 2009, ISBN 978-3-540-92811-9 .
-
László Fuchs : Abelian Groups. (= Springer Monographs in Mathematics ). Springer International, 2016, ISBN 978-3-319-19421-9 .
-
Friedrich Kasch : modules and rings. Teubner, Stuttgart 1977, ISBN 3-519-02211-7
-
Serge Lang : Algebra (= Graduate Texts in Mathematics. Volume 211). 3rd, revised. Edition. Springer, New York NY a. a. 2002, ISBN 0-387-95385-X .
-
Stephan Rosebrock : Illustrative group theory - a computer-oriented geometrical introduction. 3rd revised edition, Springer Spectrum, Berlin 2020, ISBN 978-3-662-60786-2 .
Individual evidence
-
↑ Làzlò Fuchs: Abelian Groups Springer, ISBN 978-3-319-19421-9 , p. 1.
-
↑ Lazlo Fuchs: Abelian Groups Springer, ISBN 978-3-319-19421-9 , page 2.
-
↑ Làzlò Fuchs: Abelian Groups Springer, ISBN 978-3-319-19421-9 , p. 3.
-
^ Andreas Bartholomé, Josef Rung, Hans Kern: "Number theory for beginners" Vieweg + Teubner, 7th edition, 2010, ISBN 978-3-8348-1213-1 , page 44ff
-
↑ Làzlò Fuchs: Abelian Groups Springer, ISBN 978-3-319-19421-9 , page 6.
-
^ Friedrich Kasch: Modules and Rings. Teubner, Stuttgart 1977, page 55, ISBN 3-519-02211-7
-
^ Friedrich Kasch: Modules and Rings. Teubner, Stuttgart 1977, page 57, ISBN 3-519-02211-7
-
^ Friedrich Kasch: Modules and Rings. Teubner, Stuttgart 1977, page 58, ISBN 3-519-02211-7
-
↑ Làzlò Fuchs: Abelian Groups Springer, ISBN 978-3-319-19421-9 , p. 217.
Web links


























































































































![{\ displaystyle (a + b) {\ bmod {1}} = (a + b) - [a + b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a6bfda6fe0f4841b37d7dc970fa12da26492f6c7)
![{\ displaystyle [x]: =}](https://wikimedia.org/api/rest_v1/media/math/render/svg/206831957ac1c70e1ff5ad33a9ddd67db59ca361)





























































![{\ displaystyle A [n]: = \ {a | a \ cdot n = 0 \}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ef0c387c0333813d410533184a75b54b873aeb62)
![{\ displaystyle T (A): = \ sum \ limits _ {n \ in \ mathbb {N}} A [n] = \ {a | a \ in A {\ text {there are}} n \ in \ mathbb {N} {\ text {with}} a \ cdot n = 0 \}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d4ad1ce0af1ee1d1aef7e5e5e47a8edb05082d45)