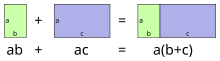
Distributive law
The distributive laws (lat. Distribuere "distribute") are mathematical rules that indicate how two two- digit links relate to each other when brackets are broken, namely that one link is compatible in a certain way with the other link .
In school mathematics in particular, the use of the distributive law to convert a sum into a product is referred to as factoring out or singling out. Solving parentheses by applying the distributive law is known as multiplying .
The distributive law, together with the associative law and the commutative law, form fundamental rules of algebra .
Formal definition
Let two two- digit links and be defined on a set . The link is called
- linksdistributiv about if for all true
- rechtsdistributiv about if for all true
- distributive over if it is left and right distributive over .
If the connection is commutative, then these three conditions are equivalent .
meaning
The two-digit links for the addition and multiplication of numbers can serve as an example .
A distinction between linksdistributiven and rechtsdistributiven links:
- (left-hand distribution)
- (legal distributive)
In words:
- A sum (or difference) is multiplied by a factor by multiplying each summand (or minuend and subtrahend) with this factor and adding (or subtracting) the product values.
If the “superordinate” link, in this case the multiplication, is commutative , one can infer from the left distributivity also the right distributivity and vice versa.
An example of "only" legal distributivity is division , which is not commutative:
The following generally applies here:
In school mathematics, mostly only the bilateral (commutative) distributive laws are designated as such and the law of division is circumvented. It is then only calculated:
- be and
The distributive laws are among the axioms for rings and bodies . Examples of structures in which two functions are distributively related to one another are Boolean algebras , such as the algebra of sets or the switching algebra . But there are also combinations of links that are not distributively related to one another; for example, addition is not distributive to multiplication.
The multiplication of sums can also be put into words as follows: A sum is multiplied by a sum by multiplying each addend of one sum by each addend of the other sum - taking into account the signs - and adding the resulting products.
Examples
Real numbers
The following examples illustrate the use of the distributive law on the set of real numbers . In school mathematics, these examples are usually referred to as multiplying. From the point of view of algebra , the real numbers form a field , which ensures the validity of the distributive law.
- First example (mental arithmetic and writing multiplication)
In mental arithmetic, the distributive law is often used unconsciously:
You want to compute 6 · 16 in your head. To do this, multiply 6 · 10 and 6 · 6 and add the intermediate results. Even the written multiplication based on the distributive law.
- Second example (with variables)
-
- Third example (with two sums)
-
- Here the distributive law was applied twice and the result was summarized. It does not matter which bracket is multiplied out first or whether in one step each addend of the first bracket is multiplied with each addend of the second bracket. The result is the third binomial formula .
- Fourth example
- Here the distributive law is applied the other way around than in the previous examples. Consider
- Since the factor occurs in all summands , it can be excluded. That means, based on the distributive law, applies
Matrices
The distributive law is also valid for the matrix multiplication . More precisely, it applies
for all matrices and matrices as well
for all matrices and matrices . Since the commutative law does not apply to matrix multiplication , the second law does not follow from the first law. In this case there are two different laws.
See also
- Distributive Association
- Boolean algebra (classical propositional logic )
literature
- DM Smirnov: Distributivity . In: Michiel Hazewinkel (Ed.): Encyclopaedia of Mathematics . Springer-Verlag , Berlin 2002, ISBN 978-1-55608-010-4 (English, online ).