Product (math)
A product is the result of a multiplication as well as a term that represents a multiplication. The linked elements are called factors.
In this sense, a product is a representation of form
where the product of and is usually noted as.
Derived from the Latin word producere in the meaning of bringing forward , “product” is originally the name of the result of a multiplication of two numbers (from Latin: multiplicare = to multiply). The use of the painting point goes back to Gottfried Wilhelm Leibniz , the alternative symbol to William Oughtred .
Products of two numbers
Here is always , i. That is, the product of two numbers is again a number. Products are also assumed to be associative here , i.e. H.
Product of two natural numbers
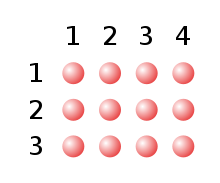
For example, if you arrange game pieces in a rectangular scheme in r rows of s pieces , you need for this
Game pieces. The multiplication is a short form for the multiple addition of r summands (corresponding to the r rows), all of which have the value s (there are s stones in each row). The total number can also be calculated by adding the number s (corresponding to the number of stones placed one behind the other in a column) r times (corresponding to the number r of such columns of stones arranged next to one another) (you need r-1 plus sign for this ). This already shows the commutativity of the multiplication of two natural numbers .
If one counts the number 0 to the natural numbers, then these form a half ring . The inverse elements regarding addition are missing for a ring : There is no natural number x with the property 3 + x = 0.
A product in which the number 0 appears as a factor always has the value zero: An arrangement of zero rows of pieces does not include a single piece, regardless of the number of pieces per row.
Product of two whole numbers
Adding the negative whole numbers gives the ring of whole numbers . Two whole numbers are multiplied by multiplying their respective amounts and adding the following sign :
In words this table says:
- Minus times minus results in plus
- Minus times plus results in minus
- Plus times minus results in minus
- Plus times plus results in plus
For a strictly formal definition of equivalence classes of pairs of natural numbers, see the article on whole numbers .
Product of two fractions
You can add, subtract and multiply without restriction in whole numbers. The division by a nonzero number is only possible if the dividend is a multiple of the divisor. This restriction can be lifted with the transition to the field of rational numbers , i.e. to the set of all fractions . In contrast to their sum, the product of two fractions does not require the formation of a main denominator :
If necessary, the result can be shortened .
Product of two real numbers
As Euclid was able to show, there is no such thing as a rational number whose square is two. Likewise, the ratio of the circumference to the diameter, i.e. the number of circles π, cannot be represented as the quotient of two whole numbers. Both “gaps” are closed by a so-called completion in the transition to the field of real numbers . Since an exact definition of the product in the brevity offered here does not seem possible, the idea is only briefly outlined:
Every real number can be understood as an infinite decimal fraction. For example, and The rational approximations - such as 1.41 and 3.14 - can easily be multiplied together. By gradually increasing the number of decimal places, a sequence of approximate values for the product is obtained - in a process that cannot be carried out in a finite time
Product of two complex numbers
Even on the set of real numbers, there are unsolvable equations such as . For both negative and positive values of , the square on the left is always a positive number. Through the transition to the body of complex numbers , which is often referred to as adjunction , i.e. adding , the so-called Gaussian number plane emerges from the real number line . Two points on this level, i.e. two complex numbers, are formally multiplied taking into account :
Geometric interpretation
A complex number can also be written in plane polar coordinates :
Is further
so it applies due to the addition theorems for sine and cosine
Geometrically, this means: multiplication of the lengths with simultaneous addition of the angles.
Product of two quaternions
Even the complex numbers can be expanded algebraically. A real four-dimensional space is created, the so-called Hamiltonian quaternions . The associated multiplication rules are presented in detail in the Quaternion article. In contrast to the above number ranges, the multiplication of quaternions is not commutative; H. and are generally different.
More examples of commutative rings
Residual classes of integers
That the product of two numbers is odd if and only if both factors are odd is a well-known fact. Similar rules also apply to divisibility by an integer N greater than two. The even numbers here correspond to the multiples of N; an even number is divisible by two with no remainder. In the case of odd numbers, one should distinguish which remainder is left after dividing this number by N as an integer. Modulo 3 - as the saying goes - there are three remainder classes of integers: Those that are multiples of three, those with a remainder of 1, and those with a remainder of 2. The product of two such numbers always has a remainder of one modulo three.
The set of these remainder classes , written, has exactly N elements. A typical element has the form and stands for the set of all integers which, when divided by N, result in the same remainder as the number a. On the set of all such remainder classes is given by
an addition and through
a multiplication explained. The resulting ring is called the remainder class ring modulo N. If and only if N is a prime number , it is actually a field. Example: modulo 5 is the residual class of 2 inversely to that of 3, since 6 modulo 5 is one. The systematic finding of multiplicative inverses modulo N is done using the Euclidean algorithm .
Function rings
If the ring R is commutative, the set (the set of all functions of a non-empty set M with values in R ) also forms a commutative ring if addition and multiplication are defined component-wise. That is, if you can
explained to everyone .
If one chooses the real numbers with the usual addition and multiplication as ring R , and as M an open subset of or more generally of , then the terms continuity and differentiability of functions make sense. The set of continuous or differentiable functions then forms a subring of the function ring , which trivially has to be commutative again if or R is commutative.
Folding product
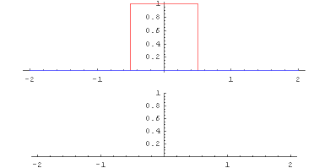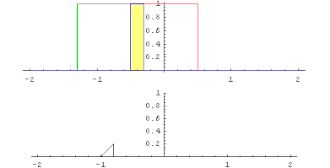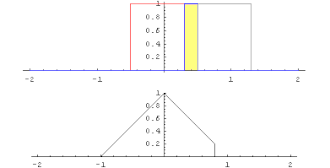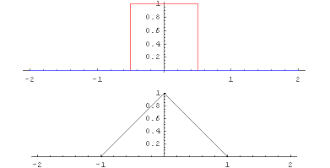
Let be two integrable real functions, whose absolute values have a finite improper integral :
Then the improper integral
for every real number t also finite. The function f * g defined by this is called the convolution product or the convolution of f and g. Here f * g is again integrable with a finite improper absolute value integral. Furthermore, f * g = g * f, i.e. H. the convolution is commutative.
After Fourier transformation , the convolution product is the point-by-point defined product except for a constant normalization factor (so-called convolution theorem ). The convolution product plays an important role in mathematical signal processing .
The Gaussian bell curve can be characterized by the fact that its folding with itself results in a bell curve that is somewhat wider (see here ). The central limit theorem is based on precisely this property .
Polynomial rings
The set of all polynomials in the variable X with real coefficients also forms a so-called polynomial ring . The product is calculated as follows:
With
These rings play an important role in many areas of algebra. For example, the body of the complex numbers can be elegantly defined as a factor ring .
In the transition from finite sums to absolutely convergent series or formal power series, the product discussed here becomes the so-called Cauchy product .
Products in linear algebra
The linear algebra deals with vector spaces and linear mappings between such. Various products appear in this context. In the following, the field of real numbers is mostly used as the basic field for simplification.
Scalar product
Already in the definition of a vector space V, the concept of submerged scalar multiplication on. This allows vectors to be “stretched” in general by a real factor, whereby in the case of multiplication by a negative scalar, the direction of the vector is also reversed.
The scalar product is a picture
Scalar product
The concept of a scalar product must be strictly distinguished from this . This is a bilinear mapping
with the additional requirement that is for everyone .
Therefore the expression is always calculable and provides the concept of the norm (length) of a vector.
The scalar product also allows the definition of an angle between two non-zero vectors v and w:
The polarization formula shows that such a length concept inversely always leads to a scalar product and thus also to an angle concept.
In every n- dimensional Euclidean space , an orthonormal system can be found through orthonormalization . If all vectors are represented as a linear combination with respect to an orthonormal basis , the scalar product of two such coordinate tuples can be calculated as a standard scalar product :
Cross product in three-dimensional space
In , as the standard model of a 3-dimensional Euclidean space, another product, the so-called cross product , can be defined. It does an excellent job with various problems of analytical geometry in space.
The cross product is an illustration
Like every Lie product , it is anti-commutative: in particular, is
Late product
The so-called late product - also only explained in the - is not a product of two, but three vectors. In modern parlance, it corresponds to the determinant of three column vectors written next to each other and is probably the easiest to calculate according to Sarrus' rule . Formally there is an illustration
which is still referred to as a product today, probably only for historical reasons. The Spat product clearly measures the volume of a Spat in space.
Composition of linear images
If f: U → V and g: V → W are two linear mappings , then they are executed one after the other
linear. If one denotes the set of all linear mappings from U to V , then the composition of maps yields a product
In the special case U = V = W, the so-called endomorphism ring of V.
Product of two matrices
Given are two matrices and . Since the number of columns in A is the same as the number of rows in B, the matrix product can be
form. In the special case r = s = t of square matrices, this creates the matrix ring .
Composition of linear images as a matrix product
There is a close connection between the composition of linear images and the product of two matrices. Let r = dim (U), s = dim (V) and t = dim (W) be the (finite) dimensions of the vector spaces U, V and W. Let also be a basis of U, a basis of V and a basis von W. With respect to these bases, let the representing matrix be from f: U → V and the representing matrix from g: V → W. Then is
the representative matrix of .
In other words: the matrix product provides the coordinate-dependent description of the composition of two linear maps.
Tensor product of vector spaces
The tensor product of two real vector spaces V and W is a kind of product of two vector spaces. It is therefore similar to the set theoretic product discussed below . In contrast to this, however, it is not a question of the categorical product in the category of real vector spaces. Nevertheless, it can be categorized using a universal property with regard to bilinear mapping. After that is the canonical embedding
The “mother of all products that can be defined on V and W”, so to speak. Any other real bilinear product
with values in any vector space Y comes namely by connecting a uniquely determined linear mapping
conditions.
Mapping matrices as second-order tensors
The vector space Hom (V, W) of all linear mappings between two vector spaces V and W can be interpreted in a natural (bifunctional) way as the tensor product of the dual space V * of V with W:
Here, a decomposable tensor , i.e. a functional f: V → R and a vector w in W, becomes the linear mapping g: V → W with
assigned. Can every linear mapping from V to W be obtained in this way? No, but not every tensor is decomposable either. Just as every tensor can be written as the sum of decomposable tensors, every linear mapping from V to W can also be obtained as the sum of mappings such as g defined above.
The fact that Hom (V, W) is naturally isomorphic to the tensor product of the dual space of V with W also means that the representing matrix of a linear mapping g: V → W is a simply contravariant and simply covariant tensor. This is also expressed in the transformation behavior of representational matrices when the base is changed .
Set theoretical product
The Cartesian product M x N of two sets M and N fits at first glance, not casually in the presented product term one. However, there is a connection not only in the word “product”: The product of two natural numbers m and n was explained above as the cardinality of the Cartesian product of an m-element and an n-element set. Certain forms of the distributive law also apply .
The Cartesian product is also the categorical product in the category of quantities .
Finite and infinite products
Finite products with many factors
The factorial of a natural number n (written as n! ) Describes the number of possible arrangements of n distinguishable objects in a row:
The product symbol is based on the first letter of the word product from the Greek capital letter Pi ; it is also used as a sum symbol based on the sigma .
Since the product of natural numbers is commutative, one can also use an index set (and thus leave the order of the factors undetermined)
Here is an animation of the product spelling:
The empty product
The empty product has the value one (the neutral element of the multiplication) - just as the empty sum always results in zero (the neutral element of the addition).
Infinite products
John Wallis discovered the baffling fact that
applies (compare Wallis product ). But what exactly is meant by the infinite product on the right? To do this, one considers the sequence of the finite partial products
If this sequence converges to a real number P , then one defines
A sequence of numbers is more precise . The infinite product
is called convergent if and only if the following conditions are met:
- Almost all of them are non-zero, i.e. H. there is so for all true
- the limit exists and
- this limit is different from zero.
(The validity of the last two conditions is independent of which one has chosen in the first). In this case you bet
- .
This limit value exists, because either there is at least one factor and from then on all partial products are zero or one can in the second condition o. B. d. A. choose.
Core series criterion ( convergence criterion for infinite products): The following statements are equivalent:
- An infinite product with positive nuclei converges absolutely.
- The kernel series converges absolutely.
properties
- A convergent infinite product is zero if and only if one of the factors is zero. Without the third condition, this statement would be false.
- The factors of a convergent product converge to 1 (necessary criterion).
Examples of lack of convergence
Although the sequence of partial products converges (towards zero), infinite products such as the following are not said to be convergent:
- : An infinite number of factors are zero, the first condition is violated.
- : You have to choose. But if the first factor is omitted, the partial product sequence does not converge (definitely diverges from ). The second condition is violated.
- : The sequence of the partial products converges, however towards zero, so that the third condition is violated.
These three examples also do not meet the above. necessary criterion. The product fulfills the necessary criterion, but the consequence of the partial products does not converge: The product of the first factors is .
literature
- Structure of the number system. In: dtv-Atlas zur Mathematik, Vol. 1, 2nd edition 1976, p. 52ff.
- Heinz-Dieter Ebbinghaus et al .: Numbers. Springer, Berlin 1992, ISBN 3-540-55654-0 . ( Google Books )
Extensive literature references on linear algebra can be found there .
Web links
Individual evidence
- ↑ Appearance in Albertus Magnus ' Metaphysicorum in the form productum , according to Jeff Miller: Earliest Known Uses of Some of the Words of Mathematics (P) with reference to The Oxford English Dictionary, Second Edition (accessed August 10, 2009).
- ↑ Steven Schwartzman: The words of mathematics: an etymological dictionary of mathematical terms used in English. Verlag MAA, 1994. ISBN 0-88385-511-9 . Google Books .
- ↑ product mark . In: Guido Walz (Ed.): Lexicon of Mathematics . 1st edition. Spectrum Academic Publishing House, Mannheim / Heidelberg 2000, ISBN 3-8274-0439-8 .
- ↑ Alexander Hölzle: Infinite Products. (PDF; 80 kB) May 2, 2005, accessed December 26, 2012 .











































![\ R [X]](https://wikimedia.org/api/rest_v1/media/math/render/svg/16d740527b0b7f949b4bf9c9ce004134bb490b68)


![\ R [X] / (X ^ 2 + 1)](https://wikimedia.org/api/rest_v1/media/math/render/svg/4a9561fb97d235fa5d9d975ea50b9ac958058410)

































































