Rectangular function

Rectangular function

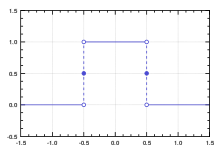
The rectangular function , also called rect function, is a discontinuous mathematical function with the following definition:

${\displaystyle \operatorname {rect} (t)=\sqcap (t)={\begin{cases}0&{\text{wenn }}|t|>{\frac {1}{2}}\\[3pt]{\frac {1}{2}}&{\mbox{wenn }}|t|={\frac {1}{2}}\\[3pt]1&{\text{wenn }}|t|<{\frac {1}{2}}.\end{cases}}}$

Alternative definitions, which are particularly common in the field of signal processing , define the rectangular function in simplified form as:

${\displaystyle \operatorname {rect_{d}} (t)={\begin{cases}1&{\text{wenn }}|t|\leq {\frac {1}{2}}\\[3pt]0&{\text{wenn }}|t|>{\frac {1}{2}}.\end{cases}}}$

General

The rectangle function can also be expressed using the Heaviside function as: ${\displaystyle \Theta (x)}$

${\displaystyle \operatorname {rect} (t)=\Theta \left(t+{\frac {1}{2}}\right)\cdot \Theta \left({\frac {1}{2}}-t\right)=\Theta \left(t+{\frac {1}{2}}\right)-\Theta \left(t-{\frac {1}{2}}\right)}$.

It is set. ${\displaystyle \Theta (0)={\tfrac {1}{2}}}$

The Fourier transformation of the rectangular function results in the sinc function : ${\displaystyle \operatorname {sinc} (x)=\sin(\pi x)/(\pi x)}$

${\displaystyle {\mathcal {F}}\{\operatorname {rect} (t)\}=\operatorname {sinc} (f)}$

This also applies to . The opposite is true ${\displaystyle \operatorname {rect_{d}} (t)}$

${\displaystyle {\mathcal {F}}\{\operatorname {sinc} (t)\}=\operatorname {rect} (f)}$.

Here it is important to use the first definition of the rectangular function, for the last equation is wrong. ${\displaystyle \operatorname {rect_{d}} }$

Shifting and scaling

A rectangular function centered at and having a duration of is expressed by ${\displaystyle t_{0}}$ ${\displaystyle T}$

${\displaystyle \operatorname {rect} \left({\frac {t-t_{0}}{T}}\right)\,.}$

Derivation

As a discontinuous function, the rectangular function is neither differentiable in the classical sense nor is it weakly differentiable . However, it is possible to derive a distribution through the Dirac delta distribution : ${\displaystyle \delta }$

${\displaystyle \operatorname {rect} '(t)=\delta \left(t+{\frac {1}{2}}\right)-\delta \left(t-{\frac {1}{2}}\right)}$

Other connections

The convolution of two equal rectangular functions results in the triangle function , the integration a ramp function . The Rademacher functions are a form with a periodic continuation of the rectangular function .

The multiple folding with folds ${\displaystyle m}$

${\displaystyle \operatorname {rect} (t)*\operatorname {rect} (t)*\operatorname {rect} (t)*\ldots }$

with a suitable scaling results in the Gaussian bell curve . ${\displaystyle m\to \infty }$

See also

• Square wave

Individual evidence

1. ^ Hans Dieter Lüke: Signal transmission. Basics of digital and analog communication systems . 6th, revised and expanded edition. Springer, Berlin et al. 1995, ISBN 3-540-58753-5 , pp. 2 .