Delta distribution

The delta distribution (also called δ-function ; Dirac function , pulse , pulse , shock (after Paul Dirac ), shock function , needle pulse , pulse function or unit pulse function ) as a mathematical term is a special irregular distribution with a compact carrier . It is of fundamental importance in mathematics and physics . Your usual formula symbol is δ (small delta).

definition

The delta distribution is a continuous linear mapping of a function space of the test functions into the underlying field : ${\displaystyle {\mathcal {E}}}$ ${\displaystyle \mathbb {K} }$

${\displaystyle \delta \colon \,{\mathcal {E}}\to \mathbb {K} \,,\,f\mapsto f(0)}$.

The test function space for delta distribution is the space of functions that can be differentiated as often as desired with or open and . Thus corresponds to either the real or the complex numbers . ${\displaystyle C^{\infty }(\Omega )}$ ${\displaystyle \Omega \subset \mathbb {R} ^{n}}$ ${\displaystyle \Omega \subset \mathbb {C} ^{n}}$ ${\displaystyle 0\in \Omega }$ ${\displaystyle \mathbb {K} }$ ${\displaystyle \mathbb {R} }$ ${\displaystyle \mathbb {C} }$

The delta distribution assigns a real or complex number to every function that can be differentiated as often as desired , namely the evaluation of the function at the position 0. The value that the delta distribution delivers after application to a test function is written (using the notation of dual pairing ) also called ${\displaystyle f}$ ${\displaystyle \delta (f)=f(0)}$ ${\displaystyle f\in {\mathcal {E}}}$

${\displaystyle \delta (f)=\langle \delta ,f\rangle =f(0)}$

or also as

${\displaystyle \delta (f)=\int _{\Omega }\delta (x)\,f(x)\,\mathrm {d} x=f(0)\,.}$

This notation is actually not correct and is only to be understood symbolically, because the delta distribution is an irregular distribution, that is, it cannot be represented by a locally integrable function in the above way. So there is no function that satisfies the above definition (for proof see “Irregularity” below). Particularly in the case of technically oriented applications of the concept, mathematically imprecise terms such as “delta function”, “Dirac function” or “impulse function” are used. When using the integral notation, it should be noted that it is not a Riemann integral or Lebesgue integral with regard to the Lebesgue measure , but rather the evaluation of the functional at the point , that is,. ${\displaystyle \delta }$ ${\displaystyle \delta }$ ${\displaystyle f}$ ${\displaystyle \delta (f)=f(0)}$

Definition via Dirac measure

The functional (for ) generated by a positive radon measure is a distribution. The delta distribution is generated by the following radon measure - we speak here specifically of the Dirac measure : ${\displaystyle \mu }$ ${\displaystyle \textstyle \langle \mu ,f\rangle =\int f(x)\,\mathrm {d} \mu }$ ${\displaystyle f\in {\mathcal {D}}}$

${\displaystyle \delta (A)={\begin{cases}1\ &{\text{falls }}0\in A\\0\ &{\text{sonst}}\end{cases}}\ ,\quad A\subset \mathbb {R} }$

A measure can be interpreted physically, e.g. B. as mass distribution or charge distribution of space. Then the delta distribution corresponds to a mass point of mass 1 or a point charge of charge 1 at the origin.

${\displaystyle \langle \delta ,f\rangle =\int f(x)\,\mathrm {d} \delta =f(0)}$

If there are point charges at the points , whereby the sum of all charges remains finite, then a measure on the algebra of all subsets of is defined, which corresponds to the charge distribution ( run through all with ): ${\displaystyle x_{i}\in \mathbb {R} }$ ${\displaystyle q_{i}}$ ${\displaystyle A\subset \mathbb {R} }$ ${\displaystyle \sigma }$ ${\displaystyle \mathbb {R} }$ ${\displaystyle i_{A}}$ ${\displaystyle i}$ ${\displaystyle x_{i}\in A}$

${\displaystyle \rho (A):=\sum _{i_{A}}q_{i}}$

The corresponding distribution for this measure is:

${\displaystyle \langle \rho ,f\rangle =\int f(x)\,\mathrm {d} \rho =\sum _{i_{A}}f(x_{i})q_{i}}$

Approximation of the delta distribution

Density of a centered normal distribution . For , the function becomes higher and narrower, but the area remains unchanged 1. ${\displaystyle \delta _{a}(x)={\tfrac {1}{{\sqrt {\pi }}a}}\cdot e^{-{\frac {x^{2}}{a^{2}}}}}$
${\displaystyle a\to 0}$

Like all other distributions, the delta distribution can also be represented as the limit value of a sequence of functions . The set of Dirac sequences is the most important class of function sequences with which the delta distribution can be represented. However, there are other consequences that converge against the delta distribution.

Dirac episode

A sequence of integrable functions is called a Dirac sequence, if ${\displaystyle (\delta _{k})_{k\in \mathbb {N} }}$ ${\displaystyle \delta _{k}\in L^{1}(\mathbb {R} ^{n})}$

1. for all and all the condition ${\displaystyle x\in \mathbb {R} ^{n}}$ ${\displaystyle k\in \mathbb {N} }$ ${\displaystyle \delta _{k}(x)\geq 0\,,}$
2. for all the identity and ${\displaystyle k\in \mathbb {N} }$ ${\displaystyle \int _{\mathbb {R} ^{n}}\delta _{k}(x)\,\mathrm {d} x=1}$
3. equality for all ${\displaystyle \epsilon >0}$ ${\displaystyle \lim _{k\to \infty }\int _{\mathbb {R} ^{n}\setminus B_{\epsilon }(0)}\delta _{k}(x)\mathrm {d} x=0}$

applies. Sometimes a Dirac sequence is only understood to be a special case of the Dirac sequence defined here. If one chooses a function with for all and and sets for , then this family of functions fulfills properties 1 and 2. If one considers the limit value instead , then property 3 is also fulfilled. This is why the family of functions is also called the Dirac sequence. ${\displaystyle \phi \in L^{1}(\mathbb {R} ^{n})}$ ${\displaystyle \phi (x)\geq 0}$ ${\displaystyle x\in \mathbb {R} ^{n}}$ ${\displaystyle \textstyle \int _{\mathbb {R} ^{n}}\phi (x)\mathrm {d} x=1}$ ${\displaystyle \delta _{\epsilon }(x):=\epsilon ^{-n}\phi ({\tfrac {x}{\epsilon }})}$ ${\displaystyle \epsilon >0}$ ${\displaystyle \epsilon \to 0}$ ${\displaystyle k\to \infty }$ ${\displaystyle \delta _{\epsilon }}$

Remarks

The function can now be used with a regular distribution ${\displaystyle \delta _{k}}$

${\displaystyle \delta _{k}(f):=\langle \delta _{k},f\rangle :=\int _{\mathbb {R} ^{n}}\delta _{k}(x)\,f(x)\,\mathrm {d} x}$

identify. Only in Limes do you get the unusual behavior of the delta distribution ${\displaystyle k\to \infty }$

${\displaystyle \lim _{k\to \infty }\delta _{k}(f)=\lim _{k\to \infty }\langle \delta _{k},f\rangle =f(0)=\langle \delta ,f\rangle }$

It should be noted that the Limes formation does not take place below the integral, but before it . If you were to pull the limit below the integral, almost everywhere would be zero, just not at . However, a single point has Lebesgue measure zero and the whole integral would vanish. ${\displaystyle \delta _{\epsilon }}$ ${\displaystyle x=0}$

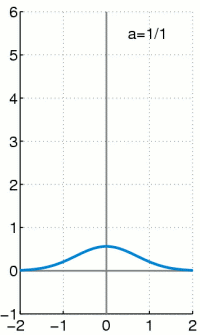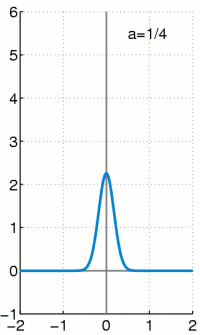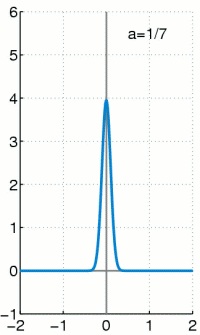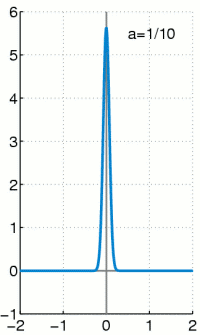
The delta distribution is clearly imagined as an arbitrarily high and arbitrarily narrow function that includes an area with a size of 1 area unit above the x-axis. You now let the function become ever narrower and therefore ever higher - the area below must remain constant at 1. There are also multi-dimensional Dirac distributions, these clearly become multi-dimensional "clubs" with a volume of 1.

Examples of Dirac sequences

Various approximations (Dirac sequences) are given below, initially continuously differentiable: ${\displaystyle \delta _{\epsilon }(x)}$

• Bell functions (normal distributions)

${\displaystyle \delta _{\epsilon }(x)={\frac {1}{\sqrt {2\pi \epsilon }}}\,\exp \left(-{\frac {x^{2}}{2\epsilon }}\right)}$

The specified functions have a very narrow and very high maximum at x = 0 , the width is approximately and the height approximately . For all of them the area is under function 1. ${\displaystyle {\sqrt {\epsilon }}\to 0}$ ${\displaystyle 1/{\sqrt {\epsilon }}\to \infty }$ ${\displaystyle \epsilon }$

• Lorentz curves

${\displaystyle \delta _{\epsilon }(x)={\frac {1}{\pi }}{\frac {\epsilon }{x^{2}+\epsilon ^{2}}}}$

• Fresnel representation

${\displaystyle \delta _{\epsilon }(x)={\frac {1}{\sqrt {i\pi \epsilon }}}\,\exp \left({\frac {ix^{2}}{\epsilon }}\right)}$

which can be imagined as a line that is wound on a cylinder, the windings of which become increasingly narrower as a result; the base area (in - -orientation) of the cylinder is formed from the imaginary and real part of the function, the function then develops in -direction. ${\displaystyle x^{2}}$ ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle z}$

However, approximations are also possible that are only piecewise continuously differentiable:

• Rectangular function

${\displaystyle \delta _{\epsilon }(x)={\frac {{\textrm {rect}}(x/\epsilon )}{\epsilon }}={\begin{cases}{\frac {1}{\epsilon }}&\ |x|\leq {\frac {\epsilon }{2}}\\0&\ {\text{sonst}}\end{cases}}}$

• Triangle function

${\displaystyle \delta _{\epsilon }(x)={\begin{cases}{\frac {\epsilon +x}{\epsilon ^{2}}}&\ -\epsilon \leq x\leq 0\\{\frac {\epsilon -x}{\epsilon ^{2}}}&\ 0<x\leq \epsilon \\0&\ {\text{sonst}}\end{cases}}}$

• Exponential function falling around the origin

${\displaystyle \delta _{\epsilon }(x)={\frac {1}{2\epsilon }}\exp \left(-{\frac {|x|}{\epsilon }}\right)}$

Further examples

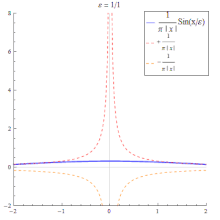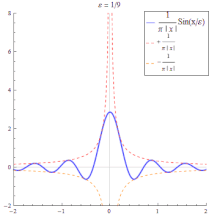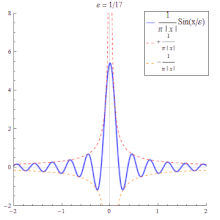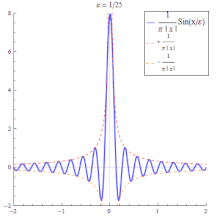
Approximation by the sinc function

• The sequence of functions of the sinc functions

${\displaystyle \delta _{\epsilon }(x)={\frac {1}{\pi x}}\sin \left({\frac {x}{\epsilon }}\right)}$
is not a Dirac sequence because its terms also take negative values. However, if you look at the expression

${\displaystyle \lim _{\epsilon \to 0}\int _{-\infty }^{\infty }{\frac {1}{\pi x}}\sin \left({\frac {x}{\epsilon }}\right)\phi (x)\mathrm {d} x}$

so for all this sequence converges in the distributional sense against the delta distribution. ${\displaystyle \phi \in {\mathcal {D}}}$

Definition in non-standard analysis

In nonstandard analysis , a “delta function” can be explicitly defined as a function with the desired properties. This is also infinitely differentiable . Your first derivative is

${\displaystyle {\frac {\textrm {d}}{{\textrm {d}}x}}\delta (x)=-{\frac {\delta (x)}{x}}}$

and their -th derivative ${\displaystyle n}$

${\displaystyle {\frac {{\textrm {d}}^{n}}{{\textrm {d}}^{n}x}}\delta (x)=(-1)^{n}{\frac {n!}{x^{n}}}\delta (x).}$

properties

• : Defining characteristic of the delta function convolution property , including selective property , Siebeigenschaft called

${\displaystyle \langle \delta ,f\rangle =\int _{-\infty }^{\infty }\delta (x)\,f(x)\,\mathrm {d} x=f(0)}$

or with the properties translation and scaling (see below) follows:

${\displaystyle \int _{-\infty }^{\infty }f(x)\,\delta (x-a)\,\mathrm {d} x=\int _{-\infty }^{\infty }f(x)\,\delta (a-x)\,\mathrm {d} x=f(a),}$

especially for the case of the constant function 1:

${\displaystyle \int _{-\infty }^{\infty }\delta (x-a)\,\mathrm {d} x=1}$

• Linearity:

${\displaystyle \langle \delta ,f+g\rangle =\langle \delta ,f\rangle +\langle \delta ,g\rangle =f(0)+g(0)}$

• Translation:

${\displaystyle \langle \delta (\cdot -a),f\rangle =\langle \delta ,f(\cdot +a)\rangle =f(a)}$

the term is also used for . ${\displaystyle \delta (\cdot -a)}$ ${\displaystyle \delta _{a}}$

• Scaling:

${\displaystyle \langle \delta (a\cdot ),f\rangle ={\frac {1}{|a|}}\langle \delta ,f({\tfrac {\cdot }{a}})\rangle ={\frac {1}{|a|}}f(0)}$

and

${\displaystyle \delta (\alpha x)={\frac {1}{|\alpha |}}\delta (x)}$

that is, the delta distribution is positively homogeneous of degree −1.

• dimension

A direct consequence of the scaling property is the dimension or unit of measurement of the delta distribution. It corresponds exactly to the reciprocal dimension of their argument. Has , for example, the dimension of a length , so has the dimension (1 / length). ${\displaystyle x}$ ${\displaystyle \delta (x)}$

• One behind the other:

${\displaystyle \int _{-\infty }^{\infty }\phi (x)\,\delta (g(x))\,\mathrm {d} x=\sum _{i=1}^{n}\int _{-\infty }^{\infty }\phi (x){\frac {\delta (x-x_{i})}{|g'(x_{i})|}}\,\mathrm {d} x=\sum _{i=1}^{n}{\frac {\phi (x_{i})}{|g'(x_{i})|}},}$

${\displaystyle \delta (g(x))=\sum _{i=1}^{n}{\frac {\delta (x-x_{i})}{|g^{\prime }(x_{i})|}}}$

where are the simple zeros of (if only has finitely many and only simple zeros). The calculation rule thus follows as a special case ${\displaystyle x_{i}}$ ${\displaystyle g(x)}$ ${\displaystyle g(x)}$

${\displaystyle \delta (x^{2}-\alpha ^{2})={\frac {1}{2|\alpha |}}[\delta (x-\alpha )+\delta (x+\alpha )],}$

irregularity

The irregularity (= singularity) of the delta distribution can be shown with a contradiction proof:

Suppose would be regular, then there would be a locally integrable function , ie a function that compact over each interval with respect. The Lebesgue measure can be integrated ${\displaystyle \delta }$ ${\displaystyle \delta (x)\in L_{lok}^{1}}$ ${\displaystyle [a,b]}$

${\displaystyle \int _{a}^{b}|\delta (x)|\mathrm {d} x<\infty }$

so that applies to all test functions : ${\displaystyle f(x)}$

${\displaystyle \langle \delta ,f\rangle =\int _{-\infty }^{\infty }\delta (x)\,f(x)\,\mathrm {d} x=f(0)}$

In particular, this must apply to the following test function with a compact carrier : ${\displaystyle \phi _{b}(x)}$ ${\displaystyle [-b,b]}$

${\displaystyle \phi _{b}(x)={\begin{cases}\exp({\frac {b^{2}}{x^{2}-b^{2}}})&|x|<b\\0&|x|\geq b\end{cases}}}$

The effect of the delta distribution on this is:

${\displaystyle \langle \delta ,\phi _{b}\rangle =\phi _{b}(0)=\exp(-1)=\mathrm {const} _{\,b}}$

With the assumed regular distribution

${\displaystyle \langle \delta ,\phi _{b}\rangle =\int _{-\infty }^{\infty }\delta (x)\,\phi _{b}(x)\,\mathrm {d} x=\int _{-b}^{b}\delta (x)\,\phi _{b}(x)\,\mathrm {d} x}$

the following estimate can be made:

${\displaystyle \phi _{b}(0)=|\langle \delta ,\phi _{b}\rangle |=\left|\int _{-b}^{b}\delta (x)\,\phi _{b}(x)\,\mathrm {d} x\right|\leq \underbrace {\|\phi _{b}(x)\|_{\infty }} _{\phi _{b}(0)}\,\int _{-b}^{b}|\delta (x)|\,\mathrm {d} x{\underset {(b<b_{c})}{<}}\phi _{b}(0)}$

Because the integral for (where is a critical value dependent on the function ) becomes smaller than 1 (and converges to 0 for to 0). One receives , therefore, a contradiction; thus the delta distribution cannot be represented by a locally integrable function. The contradiction arises because the set {0} is negligible for the Lebesgue measure, but not for the Dirac measure. ${\displaystyle \delta (x)\in L_{lok}^{1}}$ ${\displaystyle \textstyle \int _{-b}^{b}|\delta (x)|\,\mathrm {d} x}$ ${\displaystyle b<b_{c}}$ ${\displaystyle b_{c}}$ ${\displaystyle \delta (x)}$ ${\displaystyle b}$ ${\displaystyle \phi _{b}(0)<\phi _{b}(0)}$

Derivatives

Derivation of the delta distribution

Like any distribution, the delta distribution can be differentiated distributively as often as required:

${\displaystyle \langle \delta ',f\rangle =-\langle \delta ,f'\rangle =-f'(0)}$

And the -th distributive derivative: ${\displaystyle n}$

${\displaystyle \langle \delta ^{(n)},f\rangle =(-1)^{n}\langle \delta ,f^{(n)}\rangle =(-1)^{n}f^{(n)}(0)}$

Derivation of the Dirac sequence

The derivatives of the regular distributions can be calculated using partial integration (here as an example for the first derivative, analogously for higher) ${\displaystyle \delta _{\epsilon }}$

${\displaystyle {\begin{aligned}\langle \delta _{\epsilon }^{\prime },f\rangle &=\int _{-\infty }^{\infty }\delta _{\epsilon }^{\prime }(x)\,f(x)\,\mathrm {d} x\\&=\underbrace {\left[\delta _{\epsilon }(x)\,f(x)\right]_{-\infty }^{\infty }} _{=0}-\int _{-\infty }^{\infty }\delta _{\epsilon }(x)\,f^{\prime }(x)\,\mathrm {d} x\\&=-\int _{-\infty }^{\infty }\delta _{\epsilon }(x)\,f^{\prime }(x)\,\mathrm {d} x\\&=-\langle \delta _{\epsilon },f^{\prime }\rangle \end{aligned}}}$

and result in the behavior of the distributive derivative in the Limes : ${\displaystyle \epsilon \to 0}$

${\displaystyle \lim _{\epsilon \to 0}\langle \delta _{\epsilon }^{\prime },f\rangle =-f^{\prime }(0)=\langle \delta ^{\prime },f\rangle }$

Derivation of the Heaviside distribution

The Heaviside function is not continuously differentiable, but the distributive derivative does exist, namely the delta distribution: ${\displaystyle \Theta (x)}$

${\displaystyle \langle \Theta ',f\rangle =-\langle \Theta ,f'\rangle =-\int _{-\infty }^{\infty }\Theta (x)\,f'(x)\,\mathrm {d} x=-\int _{0}^{\infty }f'(x)\,\mathrm {d} x=-\underbrace {f(\infty )} _{=0}+f(0)=\langle \delta ,f\rangle }$

Since the Heaviside distribution does not have a compact carrier, the test functions here have to be differentiable functions with a compact carrier as often as desired , that is, they must vanish into infinity. ${\displaystyle f\in C_{0}^{\infty }\cong {\mathcal {D}}}$ ${\displaystyle f}$

Fourier-Laplace transform

Since the delta distribution has a compact carrier, it is possible to form the Fourier-Laplace transform of this. For this applies

${\displaystyle {\hat {\delta }}=1\,.}$

Fourier transform

The Fourier-Laplace transformation is a special case of the Fourier transformation and therefore also applies

${\displaystyle {\mathcal {F}}(\delta )(\phi )=\delta ({\mathcal {F}}(\phi ))=\delta \left(\int _{-\infty }^{\infty }e^{-ix\xi }\phi (x)\mathrm {d} x\right)=\langle 1,\phi \rangle \,.}$

There is also a convention of multiplying the factor by the Fourier transform. In this case, the result of the Fourier transformation is also the delta distribution. The result of the transformation clearly means that the delta distribution contains all frequencies with the same strength. The representation (or with the other convention for the prefactor) is an important representation of the delta distribution in physics. ${\displaystyle {\tfrac {1}{\sqrt {2\pi }}}}$ ${\displaystyle {\tfrac {1}{\sqrt {2\pi }}}}$ ${\displaystyle \delta (x)={\mathcal {F}}^{-1}(1)}$ ${\displaystyle \delta (x)={\mathcal {F}}^{-1}({\tfrac {1}{\sqrt {2\pi }}})}$

Laplace transform

The Laplace transform of the delta distribution is obtained as a special case of the Fourier-Laplace transform. It also applies here ${\displaystyle {\mathcal {L}}}$

${\displaystyle {\mathcal {L}}(\delta )=1\,.}$

In contrast to the Fourier transform, there are no other conventions here.

Note regarding the representation

Often the Fourier or Laplace transform is represented by the usual integral notation. However, these representations are

${\displaystyle {\mathcal {F}}(\delta )(\xi )=\int _{-\infty }^{\infty }e^{-i\xi x}\,\delta (x)\,\mathrm {d} x}$

for the Fourier transform respectively

${\displaystyle {\mathcal {L}}(\delta )(\xi )=\int _{0}^{\infty }e^{-\xi x}\,\delta (x)\,\mathrm {d} x}$

for the Laplace transformation to be understood only symbolically and not mathematically defined.

Transformation of the shifted delta distribution

It is also possible to calculate the Fourier transformation or the Laplace transformation for the shifted delta distribution . It applies ${\displaystyle a>0}$ ${\displaystyle \delta _{a}}$

${\displaystyle {\begin{aligned}{\mathcal {F}}(\delta _{a})&=e^{-i\xi a}\\{\mathcal {L}}(\delta _{a})&=e^{-\xi a}.\end{aligned}}}$

Practical use

The Dirac collision is of practical importance in determining the impulse response in acoustics (in other branches of physics one speaks of a quantity if one thinks that the quantity in question satisfies the narrowest possible distribution). Every room has its own sound behavior. With a Dirac impulse (approximated by clapping your hands) this behavior can be determined (by measuring the “echo”, i.e. the system response ). ${\displaystyle \delta }$

Typical, technically feasible Dirac values:

• High voltage technology approx. 1–100 ns half width
• High-frequency technology approx. 10-100 ps half-width
• Pulse laser technology approx. 10–100 fs half-width

An important application of the delta distribution is the solution of inhomogeneous linear differential equations with the method of Green's function .

Multi-dimensional delta distribution

definition

In the multidimensional, the space of the test functions is the same , the space of the functions that are totally differentiable as often as desired . ${\displaystyle {\mathcal {E}}}$ ${\displaystyle C^{\infty }(\mathbb {R} ^{n})}$ ${\displaystyle f\colon \,\mathbb {R} ^{n}\to \mathbb {R} }$

The delta distribution has the following effect on the test function : ${\displaystyle f\colon \,\mathbb {R} ^{n}\to \mathbb {R} }$

${\displaystyle \delta \colon \,{\mathcal {E}}\to \mathbb {R} \,,\ f\mapsto f({\vec {0}})}$

In the informal integral notation using translation and scaling:

${\displaystyle \int f({\vec {x}})\,\delta ({\vec {x}}-{\vec {a}})\,\mathrm {d} ^{n}x=\int f({\vec {x}})\,\delta ({\vec {a}}-{\vec {x}})\,\mathrm {d} ^{n}x=f({\vec {a}})}$.

properties

The "multi-dimensional" delta distribution can be written as a product of "one-dimensional" delta distributions:

${\displaystyle \delta ({\vec {x}}-{\vec {a}})=\delta (x_{1}-a_{1})\,\delta (x_{2}-a_{2})\,...\,\delta (x_{n}-a_{n})}$.

Especially in three-dimensional there is a representation of the delta distribution, which is often used in electrodynamics to represent point charges :

${\displaystyle \delta ({\vec {x}}-{\vec {a}})=-{\frac {1}{4\pi }}\Delta {\frac {1}{\|{\vec {x}}-{\vec {a}}\|_{2}}}}$.

Delta distribution in curvilinear coordinate systems

In curvilinear coordinate systems the functional determinant

${\displaystyle \mathrm {d} ^{3}r=\mathrm {d} x~\mathrm {d} y~\mathrm {d} z=\det {\frac {\partial (x,y,z)}{\partial (a,b,c)}}~\mathrm {d} a~\mathrm {d} b~\mathrm {d} c}$

be taken into account.

The approach

${\displaystyle \delta ({{\vec {r}}-{\vec {r}}_{0}})=\gamma (a,b,c)~\delta (a-a_{0})~\delta (b-b_{0})~\delta (c-c_{0})}$

with and leads to the equation ${\displaystyle {\vec {r}}=(a,b,c)}$ ${\displaystyle {\vec {r}}_{0}=(a_{0},b_{0},c_{0})}$

${\displaystyle \int _{V}\delta ({\vec {r}}-{\vec {r}}_{0})~\mathrm {d} ^{3}r=\iiint _{V}\det {\frac {\partial (x,y,z)}{\partial (a,b,c)}}~\gamma (a,b,c)~\delta (a-a_{0})~\delta (b-b_{0})~\delta (c-c_{0})~\mathrm {d} a~\mathrm {d} b~\mathrm {d} c~{\stackrel {!}{=}}~1}$if . ${\displaystyle {\vec {r}}_{0}\in V}$

This shows that it must apply

${\displaystyle \gamma =\left(\left.\det {\frac {\partial (x,y,z)}{\partial (a,b,c)}}\right|_{{\vec {r}}_{0}}\right)^{-1}}$.

In a curvilinear coordinate system, the delta distribution must be given a prefactor that corresponds to the reciprocal of the functional determinant.

Examples

In spherical coordinates with and the following applies: ${\displaystyle {\vec {r}}=(r,\theta ,\phi )}$ ${\displaystyle {\vec {r}}_{0}=(r_{0},\theta _{0},\phi _{0})}$

${\displaystyle \delta ({\vec {r}}-{\vec {r}}_{0})={\frac {1}{r^{2}\sin \theta }}~\delta (r-r_{0})~\delta (\theta -\theta _{0})~\delta (\phi -\phi _{0})}$

In cylindrical coordinates with and the following applies: ${\displaystyle {\vec {r}}=(\rho ,\phi ,z)}$ ${\displaystyle {\vec {r}}_{0}=(\rho _{0},\phi _{0},z_{0})}$

${\displaystyle \delta ({\vec {r}}-{\vec {r}}_{0})={\frac {1}{\rho }}~\delta (\rho -\rho _{0})~\delta (\phi -\phi _{0})~\delta (z-z_{0})}$

See also

• Dirac identity
• Kronecker Delta

literature

• Dieter Landers, Lothar Rogge: Nonstandard Analysis. Springer-Verlag, Berlin a. a. 1994, ISBN 3-540-57115-9 ( Springer textbook ).
• Wolfgang Walter : Introduction to the theory of distributions. 3rd completely revised and expanded edition. BI-Wissenschafts-Verlag, Mannheim u. a. 1994, ISBN 3-411-17023-9 .
• FG Friedlander: Introduction to the Theory of Distributions. With additional material by M. Joshi. 2nd edition. Cambridge University Press, Cambridge u. a. 1998, ISBN 0-521-64015-6 .

Web links

Commons : Delta Distribution  - collection of images, videos and audio files

Individual evidence

1. ↑ Hans Wilhelm Alt: Linear Functional Analysis: An Application-Oriented Introduction . 5. revised Edition. Springer-Verlag, Berlin a. a., 2006, ISBN 3-540-34186-2 , page 109.
2. ↑ Rüdiger Hoffmann: Fundamentals of frequency analysis. An introduction for engineers and computer scientists. With 11 tables Expert Verlag , 2005, ISBN 978-3-8169-2447-0 , p. 26.
3. ↑ Wolfgang Nolting: Basic Course Theoretical Physics 3. Electrodynamics. Berlin, Heidelberg, New York: Springer, 2007, ISBN 978-3-540-71251-0 .