Half width

The half- width of a function with a maximum is the difference between the two argument values for which the function values have dropped to half of the maximum, thus the “width at half the height”.

Accordingly, the term FWHM ( Full Width at Half Maximum ) is used in English and in technology for the half- width . If the function is time dependent, the abbreviation FDHM ( Full Duration at Half Maximum ) is used.

definition

A function has a maximum. At points and the value of the function has dropped to half of the maximum: ${\ displaystyle f (x)}$ ${\ displaystyle x _ {\ mathrm {max}}}$ ${\ displaystyle x_ {1}}$ ${\ displaystyle x_ {2}}$

{\ displaystyle f (x_ {1}) = f (x_ {2}) = {\ frac {1} {2}} f (x _ {\ mathrm {max}}) \,}

.

Then the half width is the difference . ${\ displaystyle | x_ {1} -x_ {2} |}$

conversion

For a fixed function form, the half-width can be converted into differently defined widths of the function. So you can z. B. for the normal distribution, convert the FWHM and the standard deviation into each other: ${\ displaystyle \ sigma}$

{\ displaystyle \ mathrm {FWHM} = 2 {\ sqrt {2 \ ln 2}} \, \ sigma \ approx 2 {,} 3548 \ cdot \ sigma}

Peak broadening

The increase in the half-width of a peak is called peak broadening. The intensity of the peak (i.e. its integral over the size of the expansion) usually remains the same, but the peak height decreases.

Possible causes for peak broadening are e.g. B. in physics line broadening (emission lines show energetic broadening) or dispersion (wave packets dissolve over time).

Application examples

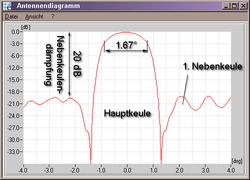
Antennas

Antenna diagram of a parabolic antenna (excerpt)

In antenna technology , the directivity factor of an antenna is specified as a half-width (or "opening angle"). What is meant here is the distance between the −3 dB limits. The half-width of the antenna in the example opposite is 1.67 °.

lighting

The radiation characteristics of a luminaire (with optics) are usually given in a simplified manner using an angle. This "radiation angle" is also the half-value angle , i. H. the full angle between the two points of a light plane at which the light intensity only reaches half of the maximum. This simplified specification is based on a light distribution curve that is rotationally symmetrical to the light axis .

Web links

Examples of half-widths of common functions (Engl.)