Symmetry (geometry)
The geometric term symmetry ( ancient Greek συμμετρία symmetria evenness, uniformity , from σύν syn "together" and μέτρον metron , measure) denotes the property that a geometric object can be mapped onto itself through movements , i.e. appears unchanged. A transformation that maps an object to itself is called a symmetry mapping or symmetry operation .
Sometimes two (or more) different geometrical objects are said to be symmetrical to one another if, viewed together, they form a symmetrical figure.
Depending on the number of dimensions considered, there are the following different symmetries:
Symmetries in the one-dimensional
In the one-dimensional, i.e. on a straight line, there is the symmetry with respect to a single point as well as the symmetry of the translation (displacement).
Symmetries in two dimensions
In two-dimensional a distinction must be made between point and axis symmetry . In addition, translation symmetries also occur here.
Rotational symmetry / rotational symmetry
A two-dimensional geometric figure then has the property of being rotationally symmetrical when the figure has a central point and the figure is mapped onto itself when it is rotated about this point. A circle or a circular ring are rotationally symmetrical in the narrower sense. A rotation through any desired angle maps it onto itself.
A figure is also called rotationally symmetrical if it can be depicted on itself by rotating it around the central point by a fixed angle with 0 ° <<360 °. The angle of rotation can only be determined by dividing the full angle by a value produced> 1, ie . This number is a measure of rotational symmetry and is also called "count". Accordingly, this symmetry is also called -numerous or -fold rotational symmetry (analogous to the English " -fold rotational symmetry") or also " -numerous rotational symmetry".
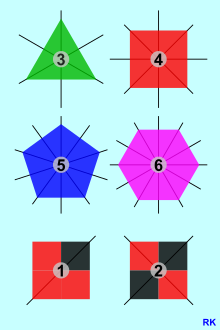
Regular polygons are typical rotationally symmetrical figures. The graphic on the right shows the first four, with the largest possible key figure of the rotational symmetry also being drawn in. In addition, two further figures are shown, namely one without and one with double rotational symmetry. In the trivial case, there is no rotational symmetry / rotational symmetry and the code number 1 is not used in the mathematical context, unless you want to identify the trivial cyclic group , which only consists of the identical mapping .
The Schoenflies symbology defines the symbol for the symmetry elements and symmetry groups of the rotational symmetry . Further examples of double rotational symmetry are the point-symmetrical figures shown below . The fact that point-symmetrical objects are always rotationally symmetrical, however, only applies in the two-dimensional.
Mirror symmetry / axis symmetry
The mirror symmetry is a form of symmetry, which occurs when objects perpendicular to an axis of symmetry mirrored (see drawing). In two-dimensional terms, it is synonymous with axial symmetry or axis symmetry . The following applies to every axis mirroring:
- Figure and picture figure are congruent with one another.
- Line and image line are of the same length.
- The angle and angle of view are the same.
- Figure and picture figure have different directions of rotation, provided that a sense of rotation is defined in the figure.
Examples
- Triangles can have one or three mirror symmetry axes: An isosceles triangle is axisymmetric to the perpendicular of the base. Homogeneous equilateral triangles have three mirror symmetry axes, as the graphic opposite shows. The fact that in these polygons shown in color the number of axes of symmetry corresponds to the number mentioned above for rotational symmetry does not apply in general, because there are many rotationally symmetrical objects that do not have mirror symmetry, for example the point-symmetrical shapes shown below .
-
Quadrilaterals can have one, two or even four mirror symmetry axes:
- At least one mirror symmetry axis has isosceles trapezoids (through the center points of the parallel sides) and dragon squares (along a diagonal).
- There are at least two mirror symmetry axes for the rectangle (the perpendiculars from opposite sides) and for the diamond (both diagonals).
- Finally, the homogeneous square is rectangle and diamond at the same time and has four mirror axes of symmetry. If it is "filled", the number can be reduced, as the adjacent graphic also shows.
- Circles and circular rings even have an infinite number of axes of symmetry, since they are symmetrical about each axis through the center point.
- Another figure with an infinite number of axes of symmetry is the straight line . Since it is infinitely long, it is symmetrical about every axis perpendicular to it and the axis lying on itself.
Axial symmetry of function graphs
A particularly popular task in school mathematics is to prove the axis symmetry for the graph of a function . This verification is particularly simple in the case of the symmetry of the y- axis of the (Cartesian) coordinate system . A function is axially symmetric to the y- axis if:
If it is valid for all x, then there is axial symmetry, that is, f is an even function .
This condition boils down to the fact that the function values for the oppositely equal arguments and must match.
More generally, the following applies: The graph of a function f is axially symmetric to the straight line with the equation if and only if the following condition is true for any values of x :
By substituting with one obtains the equivalent condition:
Point symmetry
The point symmetry , and central symmetry , is a property of geometric objects. A geometric object (e.g. a square) is called point-symmetric (in itself) if there is a point reflection that depicts this object on itself . The point at which this reflection occurs is called the center of symmetry .
Examples
- With a square there is point symmetry (in itself) if and only if it is a parallelogram . The center of symmetry in this case is the intersection of its diagonals. As special cases of the parallelogram, the rectangle , rhombus and square are also point-symmetrical.
- Each circle is (in itself) point-symmetrical to its center.
- Two circles with the same radius are point-symmetrical to one another. The center of symmetry is the midpoint of the connecting line between the two circle centers. With point symmetry, lines that are symmetrical to one another are always of the same length.
Point symmetry of function graphs
One of the most common tasks in school mathematics is to prove that the graph of a given function is point-symmetric. This proof can be provided with the following formula:
- .
If this equation is fulfilled for all x , there is point symmetry to point ( a, b ). In the special case of point symmetry around the origin (0,0) this equation is simplified to:
- .
If it is valid for all x , then there is point symmetry in relation to the coordinate origin.
Translational symmetry
Figures that are transformed into themselves by a shift or translation (which is not the identity) have a translation symmetry . They are also known as periodic .
- Figures that are translationally symmetrical must necessarily be unlimited. In applications of mathematics this is practically never the case, which is why limited subsets of periodic sets ( crystal lattices, etc.) are called periodic.
- The graphs of periodic real functions such as the sine function show a translation symmetry in one direction.
Scale symmetry
In some mathematical and physical contexts, the immutability of an object under enlargement or reduction is referred to as scale symmetry or scale invariance . This phenomenon becomes very clear in the so-called fractals .
Symmetries in three dimensions
In the nature

The physique of the vast majority of animal species and the structure of many plant organs is externally almost mirror-symmetrical - referred to in biology as bilaterally symmetrical - with a left and a right half. The only plane of symmetry (monosymmetry) is the anatomical median plane , ie the median (centrally located) sagittal plane; that is every level through the body that extends front to back and top to bottom. 95 percent of all animal species, including humans, are bilateria ("two-sided animals") with the eponymous body symmetry (the other, very original animals (e.g. jellyfish ) often have rotational symmetry with respect to a longitudinal axis, their body is therefore an approximate one Solid of revolution ). Due to the monosymmetry of the bilateria, clear planes and directions of the body can be defined, which simplifies an anatomical description. But the symmetry of the body is not perfect, so many simply occurring (unpaired) internal organs (e.g. heart) are excluded from the mirror symmetry. All symmetrically designed body parts, for example in humans eyes , ears , arms , legs , breasts , etc., each have slight deviations from one another in terms of position, shape and size.
In zoology, the five-pointed radial symmetry of echinoderms , which is unique within Bilateria, is called pentamerism (i.e. in the case of the starfish , five planes of symmetry run through the central axis of rotation). In mathematics, the symmetry properties of the starfish can be described by a rotating group . (The starfish larvae are bilaterally symmetrical, like most of the other animals in the group. The pentamerism only develops during metamorphosis .)
Without a symmetry, ie asymmetrical , the tissue-less ( sponges and placozoa ).
Correspondences to two-dimensional symmetry elements
The axis symmetry in the two-dimensional corresponds to the mirror symmetry with respect to a plane in the three-dimensional. The point symmetry in the two-dimensional corresponds to the axial symmetry (rotational symmetry around 180 °). In addition, there is point / central symmetry in space and, as in the plane, translational symmetries .
Rotational symmetry / Rotational symmetry
Three-dimensional objects are rotationally symmetrical in the narrower sense, if a rotation around any angle around an axis (the axis of symmetry) maps the object onto itself. This type of rotational symmetry about an axis is also known as cylindrical symmetry . Three-dimensional geometric objects with this property are also called bodies of revolution.
Analogous to the two-dimensional, the concept of rotational or rotational symmetry is also used when the body can be mapped onto itself by rotating through certain angles around an axis. As examples of rotationally symmetrical 3D objects, prisms are shown in perspective in the graphic opposite , which arise when the 2D polygons of the graphic above Four regular polygons and two other geometric figures with the key figures of their rotational symmetry are displaced along a straight line perpendicular to the figure become. This procedure is also called an extrusion of the polygon. Straight prisms are created, special polyhedra , which in this case, if the given polygons are regular polygons, are called regular prisms.
The center of symmetry of a 2D object becomes the axis of rotation with an arrowhead through the extrusion, which can be used to determine whether the angle of rotation is to be counted as positive or negative (see corkscrew rule ). The symmetries shown belong to the cyclic groups to and are subgroups of the respective full symmetry groups of the prisms. It should be noted that these 3D objects have additional rotational and mirror symmetries. Representing the six regular prisms shown, all rotational symmetries of a homogeneous cube are considered in the following section .
Rotational symmetries of a cube
A homogeneous cube has a total of 13 axes of rotation (axes of rotational symmetry), as shown in the graphic below:
- 3 the surfaces through the centers of opposite sides,
- 4 through opposite corners and
- 6 which run through the centers of opposite edges.
If one counts the symmetry elements of the rotational symmetry of the cube, they are: The neutral element , 3 each for 4-fold, 2 each for 3-fold and one each for 2-fold rotation axes. Overall, these are elements of symmetry.
These 24 elements together form the cube turning group . Cube and regular octahedron are dual Platonic solids and have the same symmetries. Therefore, the cube-turning group and the octahedron-turning group are dealt with together in the article Octahedron group . If you combine the rotating cube group with the point reflection at the center of the cube, elements of the full symmetry group of the cube result ( see below ).
Mirror symmetry

Mirror symmetry is used in two meanings:
- A body has mirror symmetry if there is a plane and the reflection at this plane is a symmetry operation of the body under consideration. After the reflection, the observed object is congruent with itself. The mirror plane of symmetry is also simply referred to as the mirror plane . In this sense, mirror symmetry is an automorphism . In mathematics, automorphism is a mapping of a mathematical object onto itself, in which the object and the mapped object are indistinguishable.
- Two bodies are said to be mirror-symmetrical to one another if they only differ by reflection on one plane. Colloquially one speaks of a mirror-inverted copy (or a mirror-inverted image). The position of the two bodies in space is irrelevant. It may therefore be necessary to first move and rotate before a common mirror plane can be found. The two churches of Santa Maria di Monte Santo and Santa Maria dei Miracoli on the Piazza del Popolo in Rome are (approximately) mirror-symmetrical and face each other, so that a reflection would possibly be possible without displacement. The churches would then also be mirror-symmetrical in the first meaning of the term described above. Another classic example of two mirror-symmetrical buildings are the buildings known as King Charles Court and Queen Anne Court of the Royal Naval College in Greenwich, built by Christopher Wren .
Highly symmetrical objects (like some of the prisms in the adjacent graphic) can have a large number of mirror planes that all intersect at one point. A sphere has an infinite number of mirror planes. The graphic below on the right shows four of nine mirror planes and one of the 13 axes of rotation of a homogeneous cube. The mirror planes intersect in the 4-fold axis of rotation. The symmetry shown is of the dihedral group type and is a subgroup of the cube group . The 48 symmetry elements of the cube group as a whole divide the cube into 48 (equivalent) fundamental areas .
Rotating mirror symmetry
Rotating mirror symmetry is the symmetry of a body, which is composed of two sub-operations. The first sub-operation is a rotation around an axis, the rotating mirror axis, the second a mirroring on a plane at right angles to the rotating axis, the rotating mirror plane. This plane goes through the center of symmetry, through the center of the body. If the rotating mirror plane is not a mirror symmetry plane of the body, then both sub-operations are not symmetry operations per se, but only their combination. The order of the partial operations is not important. We can also do the reflection first and then the rotation.
Rotating mirror symmetries of a cube
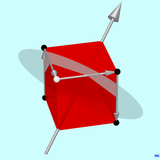
The rotational mirroring of bodies on themselves is one of the less known, but perhaps the most interesting symmetry operations that can be easily understood using suitable graphics. The three graphics show a cube and one of the rotating mirror axes and their associated rotating mirror planes. In order to distinguish the rotating mirror planes from mirror symmetry planes, they are shown as gray circular disks that appear projectively as ellipses. The semi-transparent drawing mode was selected for the graphics cubes . Since the rotating mirror axes are axes of rotation, they will be in the order of the graph above all 13 axes of rotational symmetry ... arranged.
The first of the three graphics shows one of the three 4-fold rotating mirror axes and the associated rotating mirror plane. The effect of the rotation mirroring can be understood by following the path of the corner marked with a white point. The rotating mirror plane is oriented through the rotating mirror axis. We can therefore say that the white point is above the plane of the rotating mirror. After rotating by 90 ° (right hand rule: thumb in the direction of the axis, rotation in the direction of the other fingers), the point is first mapped to the upper right corner and, by reflection, to the lower right corner, which is marked by a black point . Point and image point are connected by an arrow. The renewed rotation by 90 ° leads to the upper right black point, etc. After fourfold rotation, the starting point is reached again.
The path of a point on the cube in general position is a spatial, closed zigzag path around the plane of the rotating mirror. If the point we are tracking lies on the plane of the rotating mirror, its path is a square. If it lies on the rotating mirror axis, it jumps back and forth four times on the rotating mirror axis, mirrored by the rotating mirror plane. The center of symmetry, the center of gravity of the cube, is always mapped onto itself. Note that the rotating mirror plane is also a mirror symmetry plane of the cube in this case.
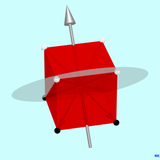
The case of one of four 6-fold rotating mirror axes shown in the second graphic is interesting. Interesting on the one hand because the rotating mirror plane is obviously not a mirror symmetry plane of the cube. On the other hand, because the 3-fold rotation axis becomes the 6-fold rotation mirror axis. You can see that it has 6 digits if you follow the path followed by a point on the cube, for example the path of the corner marked with a white point in the graphic. With the first sub-operation, a rotation of 60 ° around the rotating mirror axis, the white point is mapped to a point that is not a corner point. The second sub-operation, the mirroring on the rotating mirror plane, leads to the first image point, which is marked as a black point and which lies above the rotating mirror plane (black point at the top right). Again, point and image point are connected with an arrow. If you now apply the rotational mirroring by 60 ° again to the first image point, this leads to the second black image point at the bottom right, etc. After 6 rotational mirroring through 60 ° each, the white starting point is reached again. If the point we are tracking lies on the plane of the rotating mirror, its path is a regular hexagon .
Probably unexpected is the effect of the two-fold rotation mirroring to which the third graphic is dedicated. One of the 2-fold rotating mirror axes is shown, of which we expect six, based on the analogy of the rotating axes. If we carry out the 2-fold rotating mirroring according to the procedure outlined above, we find that each point of the cube is mapped to its " antipode ", that is, to the point on the opposite side of the cube. Point and image point lie together with the center of symmetry on a straight line and have the same distance from the center of symmetry. In this case, four white points are marked in the graphic and their pixels are marked as four black. All four connection vectors between point and image point intersect at the center of symmetry.
Also interesting is the fact that the rotating mirror images around all six possible 2-fold rotating mirror axes lead to the same type of symmetry. This type of symmetry, the point reflection at the center of symmetry, is called inversion in group theory and crystallography . In considering symmetry, one can therefore omit all 2-fold rotating mirror axes and replace them with a single operation, inversion.
A rotational mirroring leaves no point on the cube, i.e. no corner, but also no surface or edge in their original place. The only fixed point of a rotational mirroring is the center of symmetry, the center of the cube, which has already been pointed out.
A homogeneous, regular tetrahedron also has the 4-fold rotating mirror symmetry of a homogeneous cube, as the graphic shows using an axis as an example. As you can see from the graphic, in contrast to the cube, the rotating mirror plane is not a mirror symmetry plane of the tetrahedron. A wire frame model of an enveloping cube is also drawn in the graphic.
Differences between rotation mirroring and rotation
The properties of the rotating reflections differ from those of the rotations:
- Rotational axes of a body can also be rotary mirror axes of the body, but not every rotary axis is necessarily a rotary mirror axis. In the case of the tetrahedron, for example, its 3-fold axes of rotation are not axes of rotation mirror.
- The product of the symmetry operation of a rotation with itself is always a new symmetry element of the group. With an n-fold axis of rotation, the power goes up to (n-1). The product of the symmetry operation of a rotating mirror axis with itself is not a new symmetry element of the group, but a (single) rotation as a result of the double mirroring.
- The counts of an axis of rotation and a rectified rotating mirror axis can be the same (both are 4-digit in the first graphic for the cube) or they can be different (3-digit for rotational symmetry and 6-digit for rotating mirror symmetry in the second graphic).
- Each rotating mirror axis of a cube has two symmetry elements per rotating mirror axis, regardless of their number. Since the cube has three 4-digit and four 3-digit rotating mirror axes, there are rotating mirror elements of the cube group in the narrower sense. In addition, there is a point mirroring of all 2-fold rotating mirror axes, the inversion, so that a total of 15 rotating mirror elements result.
As mentioned at the beginning, the point mirroring in two-dimensional terms is equivalent to a rotation by 180 ° around the fixed point and therefore no separate symmetry element.
Point symmetry / inversion symmetry
As described in the previous section, point symmetry or inversion symmetry is the symmetry of a body with respect to a point, the center of symmetry. Each point exchanges its position with the point that is on the straight line that goes from this point through the center and is on the other side of the center at the same distance. It is a point reflection of the body on itself. The point reflection leaves no point of the body in its original place, with one exception: the only fixed point of a rotation reflection is the center of symmetry, the center of the body.
The graphic shows the mapping of four selected corners (white points) of a cube by inversion (black points). Conversely, all black points are mapped onto the white ones. The graphic is a repetition of the third graphic above ( selected rotating mirror axes ... ) without a 2-fold rotating mirror axis and rotating mirror plane.
The homogeneous Platonic solids cube , octahedron , dodecahedron and icosahedron are point-symmetric. The simplest Platonic solid, however, the regular tetrahedron , is not.
In the case of the cube (including the inversion) 15 rotating mirror symmetries had resulted. Together with the 9 mirror levels, this results in 24 symmetry elements, i.e. exactly as many as there are elements of the cube rotating group. This is no coincidence, because every mirror or rotating mirror element can be interpreted as a combination of a rotation and an inversion. In this sense, the inversion of an inversely symmetrical body has a similarly prominent position as the neutral element within a symmetry group.
Spherical symmetry
Rotational symmetry about any axis through the same point is a special case of rotational symmetry and is called spherical symmetry or radial symmetry. Stars are z. B. approximately spherically symmetrical, since their properties (such as the density) are not the same everywhere, but only depend on the distance to the center. Their gravitational fields as well as z. B. the electric field of a charged sphere are spherically symmetric.
Combinations
The symmetric basic operations can be derived from the possibility of combining symmetry operations:
- Identity (zero operation, no change)
- Rotation ( rotation )
- Rotation - Inversion ( rotation mirroring )
- Translation (displacement)
- Glide reflection
- Screwing
See also
literature
- Hermann Weyl : Symmetry: Supplemented by the text "Symmetry and Congruence" from the estate and with comments by Domenico Giulini, Erhard Scholz and Klaus Volkert. Translator Lulu Hofmann Bechtolsheim . 3. Edition. Springer Spectrum, Berlin, Heidelberg 2017, ISBN 978-3-662-52711-5 (VII, 232, limited preview in the Google book search [accessed on July 23, 2019]). Reprint of the original from 1952 in Hermann Weyl: Symmetry . Princeton University Press, Princeton, NJ 2015 (176 pp., Limited preview in Google Book Search [accessed July 23, 2019]).
- H. Schupp: Elementary Geometry . UTB Schöningh 1977, ISBN 3-506-99189-2 , pp. 35, 45.
- Will Kleber et al. : Introduction to Crystallography . 19th, improved edition. Oldenburg Verlag, Munich 2010, ISBN 978-3-486-59075-3 (470 pages, limited preview in the Google Book Search [accessed on August 18, 2019]).
- Werner Hahn: Symmetry as a development principle in nature and art . With a foreword by Rupert Riedl. Koenigstein i. Ts. ( Langewiesche publishing house ) 1989.
- MI Voitsekhovskii: Symmetry . In: Michiel Hazewinkel (Ed.): Encyclopaedia of Mathematics . Springer-Verlag , Berlin 2002, ISBN 978-1-55608-010-4 (English, /S/s091760.htm online ).
- Arthur Schoenflies: Crystal systems and crystal structure . Teubner, Leipzig 1891 (XII, 638 p., Online resources ).
Web links
Individual evidence
- ↑ The terminology is not always consistent. The rotational symmetry around a fixed angle is also called rotational symmetry in order to distinguish it from the rotational symmetry , for example that of a circle.
- ↑ Kleber 2010, p. 52
- ↑ rotational symmetry. Retrieved November 20, 2019 .
- ↑ a b Meyer's large pocket dictionary in 24 volumes . BI-Taschenbuchverlag 1992, Volume 21, p. 258.
- ↑ mirror plane in: Richard steering (ed.): Physics: Volume 2 / Ma-Z . 2nd Edition. Brockhaus, Leipzig 1989, ISBN 3-325-00192-0 , p. 909 (pages 601-1146, 48 plates).
- ↑ The obvious term car mirror symmetry, which would distinguish this mirror symmetry from the mirror symmetry in the first meaning, is not common (no hit on Google).
- ↑ Kleber 2010, p. 60 ff.
- ↑ Note that the name inversion is also used for mirroring a circle .
- ↑ Schoenflies points out on page 90 of his monograph that one should omit the twofold mirror symmetry axes , which he calls twofold symmetry axes of the second kind , and only speak of inversion: “The operation that is characteristic of the twofold symmetry axis of the second kind is inversion The axis therefore represents the same property of symmetry as a center of symmetry. For a center of symmetry, however, there is no longer any distinct direction; every twofold axis of the second kind is equivalent to it. For this reason it is advisable to leave the axes of the second kind entirely out of play; Otherwise the erroneous view could easily arise that for them too the direction represented by the axis has a special meaning for the related property of symmetry. "