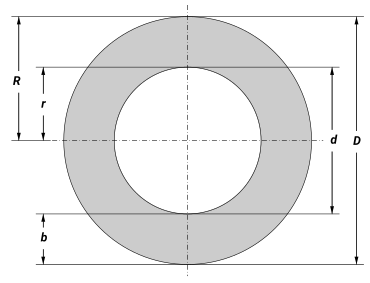
Circular ring

Circular ring with designations

A circular ring is the area between two concentric circles , i.e. H. between two circles with a common center. Its area is

{\ displaystyle A = \ pi \ cdot (R ^ {2} -r ^ {2}) = {\ frac {\ pi} {4}} \ cdot (D ^ {2} -d ^ {2})}

,

where is the number of circles and and mean the radii as well as and the diameter of the outer and inner circle. ${\ displaystyle \ pi}$ ${\ displaystyle R}$ ${\ displaystyle r}$ ${\ displaystyle D = 2R}$ ${\ displaystyle d = 2r}$

The area can also be calculated from the inside diameter or outside diameter and ring width : ${\ displaystyle d}$ ${\ displaystyle D}$ ${\ displaystyle b}$

{\ displaystyle A = \ pi \ cdot (Db) \ cdot b = \ pi \ cdot (d + b) \ cdot b}

This information can be found e.g. B. with pipe cross-sections; where is the wall thickness. ${\ displaystyle b}$

Furthermore, the area can be calculated using the annulus width and the mean annulus diameter ${\ displaystyle b}$ ${\ displaystyle d_ {m} = (D + d) / 2}$ ${\ displaystyle A}$

{\ displaystyle A = \ pi \ cdot d_ {m} \ cdot b}

.

The effective hydraulic diameter for a circular ring for hydraulic applications is ${\ displaystyle d_ {H}}$

{\ displaystyle d_ {H} = {\ frac {D ^ {2} -d ^ {2}} {D + d}} = Dd}

.

Should z. For example, for brake discs , a frictional torque to the axial force and the coefficient of friction by ${\ displaystyle M_ {t}}$ ${\ displaystyle F_ {ax}}$ ${\ displaystyle \ mu}$