Torus
A torus ( plural tori; from Latin torus here in the sense of "bulge") is a mathematical object from geometry and topology . It is a “bead-like” surface with a “hole”, so it has the shape of a tennis ring, including a lifebuoy , tire or donuts .
Examples of tori embedded in three-dimensional space are the rotation gates. Rotation gates are surfaces of revolution that are obtained by rotating a circle around an axis that lies in the plane of the circle and does not intersect the circle. If you rotate not only the circular line but the entire circular area, you get a full torus .
A Rotationstorus from that set of points In other words, formed, by a circular line of radius the fixed distance to have.
A torus can also be constructed by identifying the sides of a parallelogram. The right edge of the parallelogram is stitched to its left edge and the top to the bottom edge. Many computer games also use this topology: If a game object leaves the playing field on one side, it reappears on the opposite side.
Both constructions are special cases of the general mathematical definition, which defines a torus as the topological product of two circles. This term plays a role in numerous areas of mathematics. In addition to topology and differential geometry, it is important in Fourier analysis, the theory of dynamic systems (“invariant tori” in celestial mechanics), function theory and the theory of elliptic curves.
Rotation gates provide a concrete (rotationally symmetrical) realization of this surface in three-dimensional Euclidean space. Embedding other than a flat torus in four-dimensional space is important for many applications in theoretical mathematics and physics. This has zero curvature and the maximum possible symmetry.
The torus is a two-dimensional surface . In mathematics, one also considers the -Torus more generally, a -Dimensional manifold that generalizes the two-dimensional torus . In contrast to this, the German-language literature occasionally also uses the terms double torus, triple torus, etc. for areas with two, three and more holes.
Torus as a surface of revolution
A Rotationstorus is a surface of revolution generated by rotating a circle about an in-plane circle and the circle not intersecting the axis of rotation. A torus of rotation can be described as a set of points that are at a fixed distance from a circular line with a radius , where is. In Cartesian coordinates , with the z-axis as the axis of rotation and the centers of the rotating circle in the xy-plane, it is given by the equation
described. Eliminating the root yields the 4th degree equation
A toroidal coordinate and a poloidal coordinate perpendicular to it can be introduced into the toroidal surface . The torus is imagined to have been created by a circle that is rotated around an axis lying in the plane of the circle. We call the radius of the original circle , this circle also forms a coordinate line of . We call the distance of the center of the circle from the axis , the coordinate lines of are circles around the axis of rotation. Both coordinates are angles and run from to .
Parameterization of the torus
The conversion of torus coordinates into Cartesian coordinates is
Toroidal coordinates are important in nuclear fusion technology, see nuclear fusion reactor .
Surface of the torus
The surface of the torus with the parametric representation above is
This formula can either be derived from Guldin's First Rule
or with the help of the surface integral
to calculate. It is the surface element of the torus in the above parameter representation.
The torus borders a 3-dimensional full torus . The volume of the full torus is ( according to Guldin's Second Rule ).
Plane sections of a torus
- Sections with planes that contain the axis of rotation are pairs of circles.
- Sections with planes that are perpendicular to the axis of rotation are pairs of circles or a circle or empty.
- A plane parallel to the axis of rotation cuts a spiral curve from a torus . In special cases this can be a Cassini curve .
- An inclined plane that touches two producer circles cuts out Villarceau circles .
Tori in Descriptive Geometry
In descriptive geometry , parts of a torus are used to construct transition surfaces between cylinders . The representation of a torus through its outline can be found in outline constructions .
General definition of a torus
With become the county (the 1-sphere called). The torus is then defined by
- ,
where is the product of topological spaces . The surface of revolution described in the previous section is a 2-torus. The 2-torus is usually simply called the torus.
properties
Structure of a manifold
The torus is a topological manifold . This follows from the fact that the torus is the topological product of 1-spheres and the 1-sphere itself is a topological manifold. The 1-sphere is also a differentiable manifold and, since the product of differentiable manifolds results in a differentiable manifold, the torus is also a differentiable manifold. The dimension of is the same .
Topological properties
It also follows directly from the definition that the torus is compact . Besides, it's path-related . In contrast to the sphere, the torus is not simply connected for .
The mapping , defined by , is the universal overlay of the torus.
Lie group
The 1-sphere, understood as a circle group , is also a Lie group . Since the product of several Lie groups with the component-wise multiplication is again a Lie group, the -Torus is also a Lie group.
Embedded tori
Flat tori
Since the circular line can obviously be embedded in the , the torus can be understood as a subset of Euclidean space . One looks at the Riemannian metric which is induced by the Euclidean metric of space on the torus. This metric is flat , that is, the torus is locally isometric to a neighborhood of the . In particular, its cutting curvature is therefore constantly zero everywhere. Since the torus is compact and therefore complete , it is a flat manifold . One therefore speaks of a flat torus.
There are other flat metrics on the torus besides the one described above. Flat 2-tori can be described by a parallelogram, the opposite sides of which are glued together. Equivalently, flat tori can be described as topological groups of factors for two linearly independent vectors . In the special case and one obtains the quotient .
Elliptic curves over the complex numbers can be represented by means of the Weierstrassian parameterization as for a grid and are therefore (with a translation-invariant metric) examples of flat tori. The module space of the elliptical curves or equivalent of the flat 2-tori is the so-called module curve .
Flat tori in 3-dimensional space
A 2-times differentiable embedding of the torus in the 3-dimensional space cannot be flat, because the local extrema must be points of positive curvature. According to Nash's embedding theorem , however, there are “fractal” (only 1-times differentiable) embeddings of the flat torus in 3-dimensional space. These can also be constructed numerically.
Rotation gate in 3-dimensional space
A torus of rotation is an embedded 2-torus, which can be described as a set of points that have a fixed distance from a circular line with a radius , where is.
Clifford Tori
A Clifford torus is a special torus embedded in it. After identifying and the standard Cliffordtorus can be described as
- .
Furthermore, the images of under isometrics of the standard metric are referred to as Clifford tori.
Using stereographic projection , one can also understand Clifford tori as being embedded in the tori.
A Clifford torus is a minimal area with respect to the standard metric on the . The Lawson conjecture, proven by Brendle , states that every minimal surface in the embedded torus is a Clifford torus.
Construction from a square or cube
Construction of two-dimensional tori from a square or parallelogram
In contrast to the surface of a sphere , the torus can be mapped onto a flat, rectangular surface without singularities .
The right edge of the rectangle or square is stitched to its left edge and its lower edge is stitched to its upper edge. (This construction also works with any parallelogram .) Many computer games, for example Asteroids or Pac-Man , also have this topology : If a game object leaves the playing field on one side, it reappears on the opposite side.
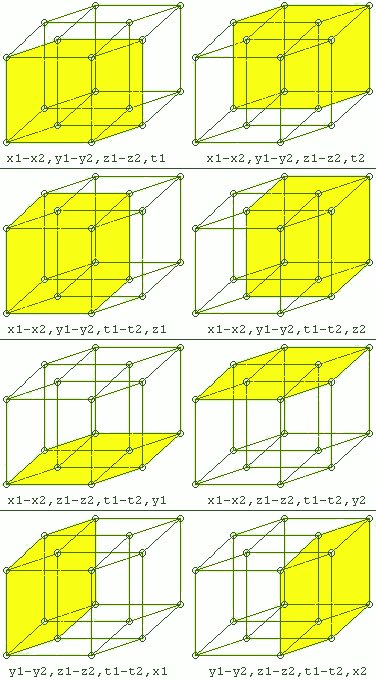
Construction of higher dimensional tori from a cube or parallelepiped
The three-dimensional torus or 3-torus is a parallelepiped or cube , the six opposite faces of which are stuck together in pairs.
The four-dimensional torus or 4-torus is a tesseract , the eight opposing cubes of which are stuck together in pairs.
In general, the -dimensional torus is a -dimensional cube , the opposing hypercubes of which are identified with each other in pairs. You can also represent it as .
Here, too, one can use any -dimensional parallelepiped instead of a -dimensional cube to construct a -dimensional torus by identifying the sides .
Algebraic torus
In algebraic group theory , the term torus is used in a different sense. A group that is isomorphic to a finite product of copies of the multiplicative group of a body is called a torus. For the purpose of delimitation, one speaks of an algebraic torus as opposed to a topological torus.
For example, in toric geometry, the study of toric varieties , the term torus usually denotes an algebraic torus.
See also
literature
- Marcel Berger : Geometry I. Translated from the 1977 French original by M. Cole and S. Levy. University text. Springer-Verlag, Berlin, 2009. ISBN 978-3-540-11658-5 .
- Anatole Katok , Vaughn Climenhaga: Lectures on surfaces. (Almost) everything you wanted to know about them. Student Mathematical Library, 46th American Mathematical Society, Providence, RI; Mathematics Advanced Study Semesters, University Park, PA, 2008. ISBN 978-0-8218-4679-7 .
Web links
- Eric W. Weisstein : Torus . In: MathWorld (English).
- Mathcurve: torus
- Math tinkering: torus
Individual evidence
- ^ Karl Ernst Georges : Comprehensive Latin-German concise dictionary . 8th, improved and increased edition. Hahnsche Buchhandlung, Hannover 1918 ( zeno.org [accessed June 26, 2019]).
- ↑ There are a number of other historical uses of the term torus that are no longer in use today : Herder 1854, Pierer 1857, Meyers 1905, Brockhaus 1911, Britannica 1911.
- ^ Bronstein, Semendjajew: Taschenbuch der Mathematik. Harri Deutsch Verlag (1983), ISBN 3871444928 , p. 253.
- ^ Ulrich Graf , Martin Barner : Descriptive Geometry. Quelle & Meyer, Heidelberg 1961, ISBN 3-494-00488-9 , pp. 202, 209.
- ↑ C. Leopold: Geometric Basics of Architectural Representation. Verlag W. Kohlhammer, Stuttgart 2005, ISBN 3-17-018489-X , pp. 123, 129.
- ^ John M. Lee: Introduction to Smooth Manifolds (= Graduate Texts in Mathematics 218. ) Springer-Verlag, New York NY et al. 2003, ISBN 0-387-95448-1 , p. 8.
- ^ John M. Lee: Introduction to Smooth Manifolds (= Graduate Texts in Mathematics 218. ) Springer-Verlag, New York NY et al. 2003, ISBN 0-387-95448-1 , p. 21.
- ↑ Tammo tom Dieck: Topology. de Gruyter, Berlin, 2000, ISBN 3-11-016236-9 , p. 52.
- ^ John M. Lee: Introduction to Smooth Manifolds (= Graduate Texts in Mathematics 218. ) Springer-Verlag, New York NY et al. 2003, ISBN 0-387-95448-1 , p. 39.
- ^ John M. Lee: Introduction to Smooth Manifolds (= Graduate Texts in Mathematics 218. ) Springer-Verlag, New York NY et al. 2003, ISBN 0-387-95448-1 , p. 289.
- ↑ V. Borrelli, p Jabrane, F. Lazarus, B. Thibert: Flat tori in three-dimensional space and convex integration. ( Memento of July 1, 2012 in the Internet Archive ). Proc. Natl. Acad. Sci. USA 109 (2012), no. 19, 7218-7223.
- ↑ CNRS press release : Mathématiques: première image d'un tore plat en 3D. April 20, 2012.
- ^ Oda: Lectures on Torus Embeddings and Applications. 1978, 1.1 Algebraic tori.























































![[0,1] ^ {n}](https://wikimedia.org/api/rest_v1/media/math/render/svg/40160923273b7109968df994dca832b91d957bf2)